基于双脉冲参量微扰的船舶运动混沌控制技术

黄 谦，李天伟，杨绍清，李正友

(1.海军大连舰艇学院 航海系，辽宁 大连116018;2.中国人民解放军91257 部队，浙江 舟山316001;3.海军大连舰艇学院 信息与通信工程系，辽宁 大连116018)

0 引 言

海上航行的船舶是在波浪环境中运动的，同时受到风、流及其他外部因素的扰动，在航行过程中必定会因为受外力的扰动而产生横摇及首摇运动，尤其是军用舰艇的这种受迫运动，对舰载武器的作战使用和特种作业必定会产生诸多不利影响，严重时甚至危及舰艇自身安全。如何避免这种情况的发生或降低船舶所受不良情况影响是船舶运动控制领域研究的一大重要课题。近年来，国内外许多学者开始采用非线性动力学理论来研究船舶的各种运动，同时，随着混沌理论在非线性研究中的出现和日益发展，人们开始将混沌理论引入对船舶非线性运动的研究之中，以便从机理及特性上对以上现象进行解释［1-9］。大量的研究表明，船舶运动中产生的非线性混沌运动是导致船舶航向无法保持或倾覆的重要因素。

目前，国内外许多学者提出了多种混沌控制方法［7-10］，张显库［7］提出利用精确反馈线性化和闭环增益成形算法相结合的非线性简捷控制方法进行船舶横摇运动的混沌控制，取得了较好的效果。李芃［8］等通过考虑设计PID 控制器使得混沌系统较快稳定到极限环上，成功抑制了混沌，但在考虑控制对象时没有考虑模型中的正弦分量影响，且没有稳定至不动点上，具有一定片面性。王林泽［10］提出用闭环反馈方式将控制目标与实测系统状态量之间的差值作用于受控系统，达到控制分叉或混沌的目的。

本文从船舶运动非线性模型角度着手，提出采用脉冲参量微扰控制混沌系统的方法，在系统参量微扰中引入脉冲控制策略实现对混沌系统的有效控制。针对所研究的某型军用舰船运动非线性模型，提出了改进的双脉冲参量微扰控制方法，将混沌系统稳定到新的周期轨道或不动点上，取得了较好的控制效果。

1 船舶运动非线性模型

1.1 模型建立

根据船舶线性操纵运动微分方程组:

式中:u0为航行速度;r 为转首角速度;v 为横漂速度;δ 为舵角;m 为船舶质量;IZ为船舶质量对通过重心铅垂轴的惯性矩。力Y 和N 及相对分量是由船舶水动力和水动力矩及舵力和舵力矩产生的。文献［9］通过对其进行变换，得到时域下船舶转首运动方程并用非线性函数H(r)=nr+qr3代替其中的一阶项r 得到非线性Bech 模型:

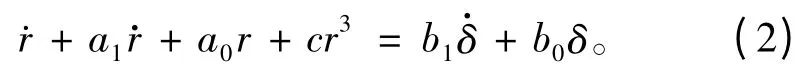
式中:a1为阻尼系数;a0为刚度系数;其余参数计算表达式参考文献［9］。根据Bech 模型，在船舶直航过程中，为模拟波浪作用，将给定值r0取为正弦函数B·sinωt，并对船舶转首角速度作比例反馈控制，即令舵角δ=kp(r0－r)，令，化简可得如下船舶运动非线性数学模型:

观察式(3)发现与受迫Duffing 方程极为相似，文献［9］指出当船的阻尼项系数和刚度项系数相差不是很大时，通过反馈增量的补偿，阻尼项系数和刚度项系数是同一数量级，在较小的给定值下，系统将进入非线性的混沌系统状态。

1.2 仿真及混沌分析

为了验证该模型是否具有混沌动力学特性，论文以某型军用舰船为研究对象，令kp=5，ω=0.60，B=0.4，计算其相应参数得出该型舰的运动非线性模型如下:

采用Matlab 7.8a 的Simulink 对模型进行仿真，仿真运行得到系统相位图，如图1所示。

图1 系统相图Fig.1 Figure of system phase

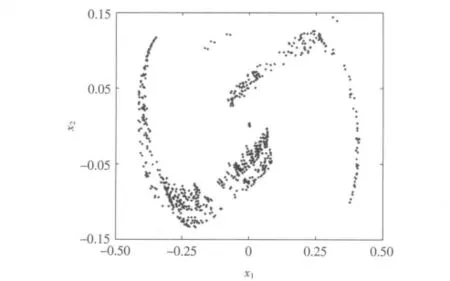
图2 Poincare 截面映射图Fig.2 Poincare section map

为了进一步验证系统的混沌特性，采用Poincare截面法，即在相空间中适当选取一截面，称为Poincare 截面，相空间的连续轨迹与Poincare 截面的交点称为截点，当Poincare 截面上是一些成片的具有分形结构的密集点时，运动便是混沌的［11］。Poincare 截面映射图如图2所示。综合以上可以发现，该模型具有较为明显的混沌特性，进一步证明了当系统参量在某一范围内时，船舶运动非线性模型会产生混沌现象。

2 基于离散脉冲参量微扰的控制方法

2.1 控制方法

依据式(4)并参考Duffing 方程，令x1=x，x2=y，a=0.30，b=4.20，γ=0.03，η=0.08，ω=0.60，δ=0.47，则式(4)可写为

由1.2 节可知，由于系统参量的变化，导致船舶产生混沌运动。若系统存在稳定的周期轨，在某一时刻参数变化后，则在原周期点系统不再保持周期运动。

研究发现，对混沌系统的参量实施脉冲微扰能实现混沌控制［10-12］，且在对实际系统的混沌控制中较易实现。本文提出将离散脉冲微扰应用于某型军用舰船运动非线性模型，实现了对连续非线性系统的混沌控制。

基于离散脉冲参量微扰的控制方法，以系统参量中某一参量λ 作为微扰对象，从时间t0开始进行控制，每隔Δt 时间，对参量λ 进行扰动，则受控系统中该参量变为如下形式:

其中:n=0，1，2，…;k 为脉冲强度;Δt 为脉冲作用时间间隔，若以系统参量δ 为微扰对象，则在t0+n·Δt 时间点上，受控系统变为如下形式:

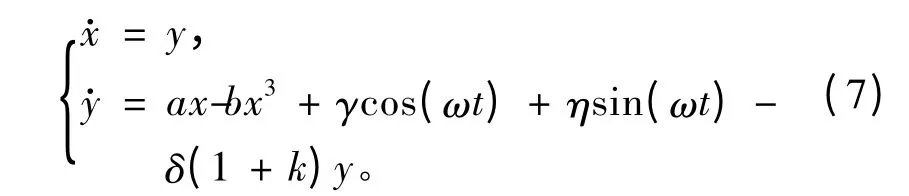
而在其余时间点上系统仍如式(5)所示。当k 和Δt取合适值时，可以把混沌系统(5)稳定到周期轨道上，故而脉冲强度k 及作用间隔时间Δt 的选取成为了实现控制的关键环节。

2.2 仿真结果

通过研究发现，对脉冲强度k 及作用时间间隔Δt 的不同取值，可以得到不同的控制效果。本文运用Matlab 的Simulink 进行控制仿真，采用四阶Runge-Kutta 方法，仿真积分步长取为0.01 s，仿真时间400 s，在t0=48 s 时加入脉冲控制。图3 和图4 为k 和Δt 不同取值条件下的仿真结果，脉冲控制参数如图3 和图4所示。

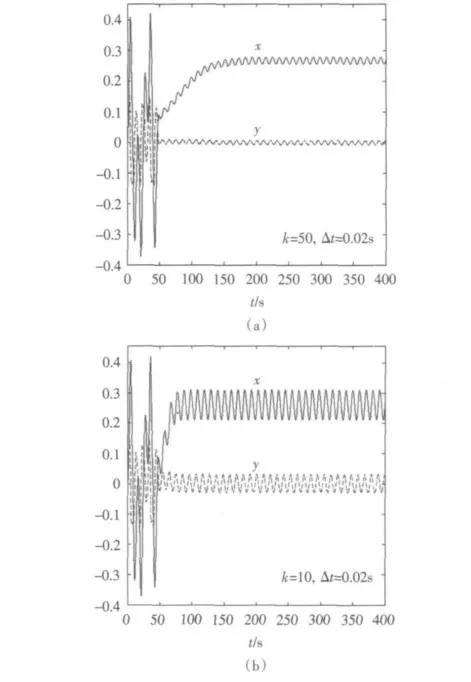
图3 系统控制仿真结果(Δt=0.02 s)Fig.3 Simulation results of pulse control(Δt=0.02 s)

通过大量仿真研究发现，采用离散脉冲对系统某一参量进行微扰，可以实现对混沌系统的有效控制，并得出以下结论:

1)当固定脉冲作用时间间隔Δt，改变脉冲强度k 时，随着k 的增大，受控系统变量振幅随之减小，但系统稳定时间增大，当k 取值很大时，系统虽然也能稳定到不动点上，但若不在不动点附近实施控制，则系统稳定到不动点时间很长，实用性不够;

2)当固定脉冲强度k，改变脉冲作用时间间隔Δt 时，随着Δt 的增大，受控系统变量振幅随之增大，但系统稳定时间减小;

3)在实际中，可以固定脉冲作用时间间隔Δt，在脉冲强度k ＞0 的范围内改变取值，就可以实现将系统稳定在P=1 到多个周期的轨道;而当取k ＜0时，系统虽然能实现稳定，但稳定后系统变量振幅很大，也就失去了控制的意义;

4)采用离散脉冲对系统某一参量进行微扰，对于控制时刻没有要求，但为得到所需控制结果，需要对脉冲强度k 及时间间隔Δt 进行参数试凑，控制的实施过程较为繁琐，且很难将系统稳定到不动点上。

图4 系统控制仿真结果(k=40)Fig.4 Simulation results of pulse control(k=40)

3 改进双脉冲参量微扰控制方法

针对采用离散脉冲对系统单一参量进行微扰实现混沌控制方法的不足，为将混沌系统尽快稳定到新的不动点上，针对所研究的某型军用舰船运动非线性模型，本文提出改进的双脉冲参量微扰控制方法，即利用离散脉冲对多个系统参量同时进行微扰，通过脉冲参数的适当选取实现对混沌系统的快速有效控制。

本文提出的改进离散脉冲参量微扰控制算法是，从时间t0开始，每隔Δt 时间对式(5)所示系统中的2个参量分别采用不同的离散脉冲进行微扰控制。对参量进行扰动时，受控参量如式(6)所示。以对系统参量a 及δ 进行微扰控制为例，则在t0+n·Δt1时间点上，受控系统变为如下形式:

在t0+n·Δt2时间点上，受控系统变为如下形式:

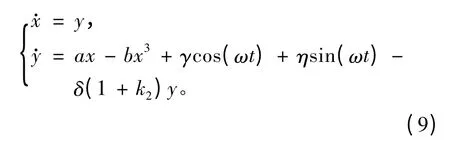
而在其余时间点上系统仍如式(5)所示。其中，k1和k2为不同脉冲的脉冲强度，Δt1和Δt2为不同脉冲对应的作用时间间隔，不同脉冲的控制参数取值可以不同，也可以相同。

为验证本文所提算法的控制效果，对受控系统进行仿真研究，用Matlab 的Simulink 进行仿真，采用四阶Runge-Kutta 方法，仿真积分步长取为0.01 s，仿真时间400 s，在t0=48 s 时加入脉冲控制。图5 和图6为k1，Δt1与k2，Δt2不同取值条件下的仿真结果，脉冲控制参数如图5 和图6所示。

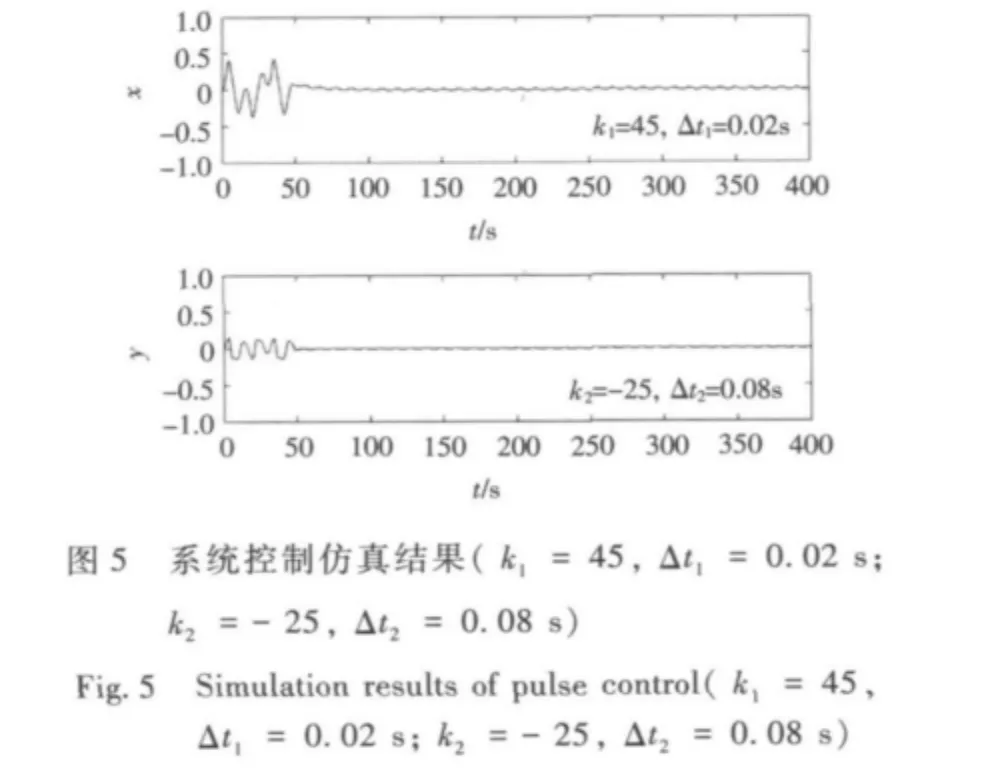
通过控制仿真研究发现，采用本文提出的改进双脉冲参量微扰控制方法进行混沌控制时，能将系统稳定在振幅较小的周期轨道或不动点上，与采用离散脉冲对单一参量进行微扰相比，其控制效果得到了明显的提高，并探索出如下规律:

1)当固定脉冲作用时间间隔为Δt，改变脉冲强度k 时，随着的增大，受控系统变量振幅随之减小，同时，系统稳定时间也随之减小;

2)当固定脉冲强度为k，改变脉冲作用时间间隔Δt 时，随着Δt 的增大，受控系统变量振幅随之增大，同时，系统稳定时间也随之增大;

3)在某型军用舰船运动非线性模型的混沌控制中，可以选择固定脉冲作用时间间隔Δt，在脉冲强度k1＞0，k2＜0 的范围内改变取值，就可以实现将系统稳定在不动点或周期轨道上;

4)采用改进的双脉冲参量微扰方法，同样对于控制时刻没有要求，但为得到所需控制结果，依然需要对脉冲强度k 及时间间隔Δt 进行参数试凑，虽然由于控制脉冲数的增加，使得控制的调整实施过程略为复杂，但对混沌系统的控制效果确实得到了很大的改进和提高。

4 结 语

本文在船舶运动混沌系统的参量控制中引入脉冲参量微扰控制策略，对船舶运动的混沌状态进行控制，并以某型军用舰船为例，对船舶运动非线性模型的离散脉冲参量微扰控制方法进行了研究，提出了改进的双脉冲参量微扰控制方法。仿真的结果表明，本文的控制方法能对连续非线性混沌系统实施有效控制，且通过对脉冲参数的调整可以实现将系统稳定在新的不动点或周期轨道上，同时也可以对控制代价和控制速度进行选择。以本文研究结果为依据设计的脉冲控制器结构简单，操作简便，具有潜在工程应用价值。

［1］刘利琴，唐友刚，吴志强.横浪中船舶的随机混沌运动［J］.工程力学，2008，25(6):204-208.

LIU Li-qin，TANG You-gang，WU Zhi-qiang.Stochastic chaotic motion of ships in beam seas［J］.Engineering Mechanics，2008，25(6):204-208.

［2］丁勇，胡开业，邱敏芝.船舶非线性横摇运动分析的Lyapunov 特性指数法［J］.中国造船，2008，49(3):1-6.

DING Yong，HU Kai-ye，QIU Min-zhi.The method of Lyapunov characteristic exponents for analyzing the stability of ship′s nonlinear roll motion［J］.Shipbuilding of China，2008，49(3):1-6.

［3］FALZARANO M，SHAW S W，TROESH A W.Application of global methods for analyzing dynamic system to ships rolling motion and capsizing［J］.Int.J.of Bifur and Chaos，1992，2(1):101-115.

［4］HU Kai-ye，DING Yong，WANG Hong-wei.Chaotic roll motions of ships in regular longitudinal waves［J］.Journal of Marine Science and Application，2010，9(2):208-212.

［5］McCUE L S.Chaotic vessel motion and capsize in beam seas［D］.Michigan:Department of Naval Architecture and Marine Engineering University Michigan，2004.

［6］WANG Ying-guang，HUANG Zhi-long，TAN Jia-hua.First passage probability of nonlinear ship rolling in radom seas［J］.Journal of Ship Mechanics，2008，12(6):870-879.

［7］张显库，王坤飞.船舶横摇运动中的混沌及其非线性简捷控制［J］.中国造船，2010，51(4):21-27.ZHANG Xian-ku，WANG Kun-fei.Chaos of ships rolling motion and its nonlinear simple and direct control［J］.Shipbuilding of China，2010，51(4):21-27.

［8］李芃，张晓宇，何晋，李文秀.船舶运动控制中的非线性混沌及PID 控制方法［J］.舰船科学技术，2002，24(5):36-39.

LI Peng，ZHANG Xiao-yu，HE Jin，LI Wen-xiu.The nonlinear chaos in ship movements control and pid controlling chaos［J］.Ship Science and Technology，2002，24(5):36-39.

［9］苏宁.混沌学与船舶运动控制［D］.大连:大连海事大学，1996.SU Ning.Chaos and ship steering control［D］.Dalian:Dalian Maritime University，1996.

［10］王林泽，赵文礼.用闭环反馈周期脉冲抑制分叉和混沌运动［J］.控制理论与应用，2006，23(3):487-490.

WANG Lin-ze，ZHAO Wen-li.Feedback-based method using periodic pulse to suppress bifurcations and chaotic motions［J］.Control Theory ＆ Applications，2006，23(3):487-490.

［11］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2002.46-56.

LV Jin-hu，LU Jun-an，CHEN Shi-hua.Analysis of chaos time series and its application［M］.Wuhan:Publishing Press of Wuhan University，2002.46-56.

［12］罗晓曙，方锦清，王力虎.一种基于间歇性正比于系统参量的脉冲微扰控制混沌方法［J］.物理学报，1999，48(12):2196-2201.

LUO Xiao-shu，FANG Jin-qing，WANG Li-hu.A method of controlling chaos based on intermitant proportional pulse perturbation to the system parameters［J］.Acta Physica Sinica，1999，48(12):2196-2201.