某型燃气轮机低压压气机转子模态及动力学分析
2012-12-02钟芳明龚建政李华志
钟芳明,龚建政,贺 星,李华志
(海军工程大学 船舶与动力学院,湖北 武汉430033)
0 引 言
燃气轮机是以连续流动的气体为工质带动叶轮高速旋转,将燃料的能量转变为有用功的动力机械,是一种旋转式热力发动机。大功率燃气轮机除可用于发电外,还可用作大型舰船动力,是国家综合实力的重要象征。作为一种典型的高速旋转机械,燃气轮机变工况运行时,转子系统常常发生振动,产生噪声,降低机组的工作效率,甚至使元件断裂、转子失稳,造成重大事故[1]。
转子动力学研究的目的和任务是为旋转机械转子的优化设计、提高效率、保证安全、减少故障和延长寿命提供理论和技术上的支持与保障。旋转机械的振动产生破坏主要因共振引起[2],各阶固有频率和振型是结构承受动力荷载设计的重要参数。当外界激振力频率与转子系统的某阶固有频率接近时,振幅会急剧增大,即振动在某些转速(临界转速)附近会因为共振而显得异常强烈。因此,合理配置转子支承系统的临界转速是保证旋转机械安全可靠运行的一项重要工作[3]。
通过对某船用燃气轮机低压压气机转子进行建模,使用数值仿真方法对其进行动力学分析,得到转子的固有模态、临界转速和稳态不平衡响应,有关结果验证了转子工作的可靠性,同时为转子的进一步优化设计提供依据。
1 基于ANSYS 的转子动力学分析
在转子动力学分析中,旋转部件的惯性效应必须自始至终予以考虑,从而达到准确预测转子振动特性的目的。惯性效应包括很重要的一点——陀螺力矩,它由转子旋转时的进动运动产生。随着转子转速的不断提高,动力学计算方程中加入陀螺效应显得不可或缺。
通过发展新单元,以达到在分析时计入科氏效应、陀螺效应和支承等因素的影响,ANSYS 很好地解决了转子动力学分析中“陀螺效应”的问题,提供了强大的分析工具。陀螺效应的考虑不受计算模型上的限制,使得其在转子动力学和整机振动分析从模型简化和建立到计算分析变得简单高效。基于ANSYS 转子动力学计算包含以下功能:
1)无阻尼临界转速;
2)不平衡响应分析;
3)阻尼特征值分析;
4)涡动和稳定性预测。
2 计算模型
该低压压气机为轴流式,9 级低压压气机采用盘鼓式结构。转子使用的材料主要为钛合金,相关材料属性杨氏模量E=1.19e11N/m,泊松比ρ=0.33,密度D=4 480 kg/m3。有2 个支承:前支承为弹性支承带挤压油膜阻尼器,安装于前机匣中;后支承为径向滚柱轴承带挤压油膜阻尼器,安装于过渡段中。
将模型文件以IGES 格式导入HyperMesh 中进行网格划分,先加以简化和几何清理,其中叶片按等效质量和等效转动惯量,以集中质量的方式加载到轮盘中。为提高精度,整个转子采用手动网格划分,单元划分为五面体和六面体,用SOLID185 单元模拟。划分好的网格模型如图1所示。

图1 转子有限元模型Fig.1 FEM model of rotor
3 计算内容及分析
3.1 模态分析
结构的固有振动特性只与结构自身的质量和刚度分布有关,因此又称自振特性。自振特性将决定结构在动力载荷下的响应行为。模态分析的主要内容是研究结构或机器部件的振动特性,得到其固有频率和振型。对复杂结构进行精确的模态分析将为评价现有结构的动态特性、诊断及预报结构系统的故障、新产品的动态性能的预估及优化设计提供科学的依据。
将划分好的有限元模型导入ANSYS 进行模态求解。为了模拟真实转子两端的支承,模型中采用连接单元COMBIN214,将转子两端的支承系统分别简化为2 个弹性-阻尼支承,单元的刚度阻尼数据参见文献[4]。求解得到转子的前8 阶固有频率,见图2。图3和图4 分别给出转子的前2 阶弯曲模态振型。
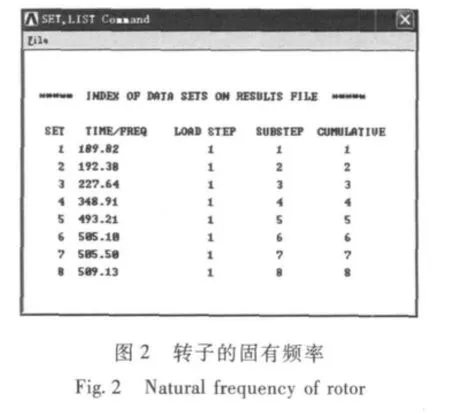

外部激励频率接近上述固有频率时,系统的振幅将出现剧烈变化,容易使整个系统受到损害。对于转子的弯曲型模态,共振将增大转静碰磨的可能性从而导致叶片损坏。转子前2 阶弯曲模态频率分别为189 Hz 和505 Hz,可见转子一阶弯曲模态频率较高,且前2 阶弯曲振型对应的固有频率值相差较大,表明转子的整体结构具备良好的刚度特性。一阶振型最大位移处在转子第4 级附近,二阶振型最大位移处在第8 级轮盘上。通过ANSYS 的动画功能可以观察转子的每一阶振型情况,见表1。

图4 二阶弯曲振型Fig.4 Second vibration shape of rotor

表1 转子的振型描述Tab.1 Vibration shapes of rotor
3.2 临界转速
在Jeffcott 转子的分析中,得到临界转速在数值上近似等于转子做横向振动时固有频率的结果[5]。在实际计算中,也常常利用这个结果,通过计算或测定转子系统的横向振动固有频率,来确定其临界转速。但是,在物理概念上不能把旋转转子的涡动与不旋转转子的横向振动混为一谈,这是2 种不同性质的物理现象[6]。事实上,由于实际转子中圆盘偏离原先平面的摆动运动会产生1 个使圆盘偏转角即轴的挠曲角发生变化的力矩,使得转子的临界转速在数值上与不计这种偏摆影响时的不同。常常把由于高速旋转圆盘的偏摆运动而使临界转速变化的现象称为陀螺效应(也称回转效应)。
3.2.1 坎贝尔图求解
许多情况下需要监测转子转速变化时频谱的几个分量的动态变化过程,以确定转子在整个转速范围内的工作特性。达到这一目的的分析方法之一就是坎贝尔图,它可以将整个转速范围内转子振动的全部分量的变化特征表示出来[7]。
在ANSYS 中,针对不同角速度下转子的多载荷步模态分析中,通过坎贝尔图可获得固有频率解,并能进一步输出受同步力或异步力的临界转速,临界转速位于频率曲线和等速线的交点处[8]。图6 为低压压气机转子的坎贝尔图。

图5 转子坎贝尔曲线Fig.5 Campell diagram of rotor
3.2.2 结果分析
由坎贝尔图解得到该燃机低压压气机转子的一阶临界转速为12 825 r/min。转子在1.0 工况下的工作转速低于一阶临界转速,其相对于临界转速的裕度大于30%,满足文献[9]关于转速偏离临界转速裕度的规定。转子的临界转速设计合理。
3.3 不平衡稳态响应
稳态不平衡响应计算是转子动力学分析中与临界转速计算同等重要的基本任务。不平衡响应分析也可以用来确定系统的临界转速,但它更重要的任务是通过求解当转子存在不平衡情况下的响应,从而得到转子不同部位对不平衡量的敏感信息,为转子下一步的平衡提供依据。
3.3.1 ANSYS 不平衡稳态响应分析的实现
在ANSYS 中,不平衡稳态响应分析是基于结构动力学分析中的谐响应分析实现的,求解方法须为完全法,且必须基于静止坐标系以便在计算中通过CORIOLIS 命令考虑科里奥利力。命令SYNCHRO 用以指定激发频率与转子的旋转同步或异步,并将旋转简谐力考虑到旋转模型中,默认的情况是与转子同步(RATIO=1),即进行不平衡响应分析。此时,只需要指定不平衡量,无需计算其与转速平方之乘积所得的不平衡力,ANSYS 会在每个频率载荷步中自动计算。对于多转子的情况,可以使用命令Cname 指定需要施加激发频率的转动部件。
3.3.2 计算结果及分析
考虑到压气机的前几级较容易出现叶片缺损,计算了依次假定在转子的第1,2,3,4,6 级轮盘(包含叶片在内,简称1,2,3,4,6 号盘)存在不平衡量时,3 个特征位置(分别取在转子的第2,4,7号盘的指定位置)的不平衡响应。假设加在不同级轮盘上的不平衡量均为1E-4 kg·m。响应图分别如图6 ~图10所示。
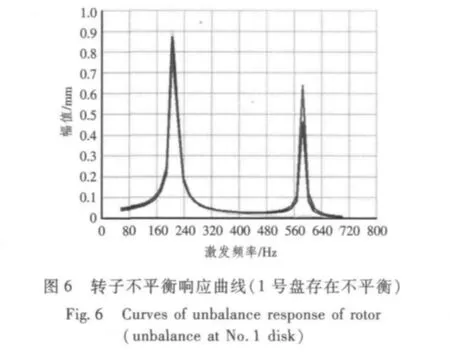
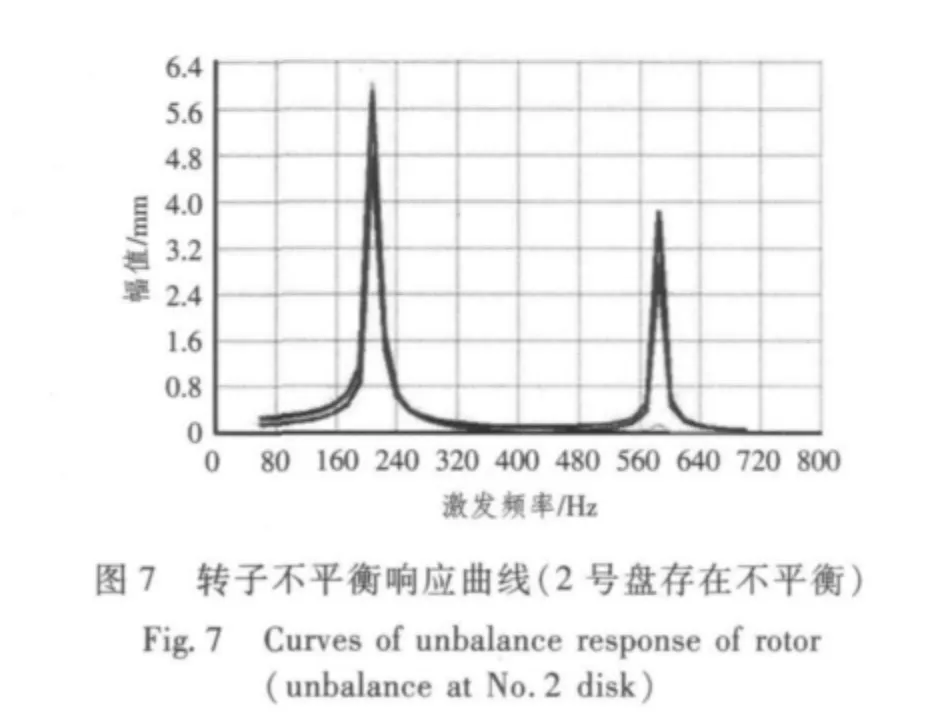
由图可得以下结论:
1)当1,2,3,4,6 号盘分别存在不平衡时,3个特征位置的一阶不平衡响应均大于二阶不平衡响应;由图9 可知,当第4 级轮盘存在不平衡时,只会激发出转子第一阶弯曲模态,不会激发第二阶弯曲模态。
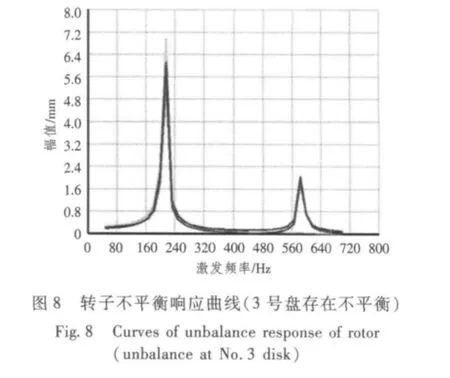


2)在所有盘存在不平衡的情况中,4 号盘在一阶临界转速下的不平衡响应幅值最大,而二阶临界转速下的响应不存在峰值。这主要取决于特征点的轴向位置和转子的振型(从图3 和图4 可知,4 号盘恰好处于一阶振型的反节点(峰值点)位置附近,而处在二阶振型的节点位置)。
3)整体观察这5 张图,转子的不平衡响应曲线较陡,在临界转速处幅值急剧上升。从前面分析已经知道,转子的一阶临界转速远大于转子1.0 工况转速,这样也就避免因为转子通过临界转速时幅值和应力过大而带来的转子支承结构疲劳等不稳定因素的问题,支承的阻尼设计也不会面临过多压力。由此可见,该转子的盘鼓式设计在减轻转子重量的同时,又提高了临界转速从而极大地避开了转子的工作转速。
将计算特征位置上的一阶和二阶不平衡响应幅值列于表2 和表3 中。

表2 一阶不平衡响应幅值Tab.2 Amplitude of first unbalance response of rotor

表3 二阶不平衡响应幅值Tab.3 Amplitude of second unbalance response of rotor
由表2 和表3 可知:
1)对于假定的所有5 个存在不平衡量的轮盘,压气机转子的一阶不平衡响应对4 号轮盘存在的不平衡最敏感(理由上文已有表述)。考虑到转子的工作转速低于一阶临界转速,其振动特性主要受第1阶振型的影响。因此,若转子在运行中因挠曲过大导致压气机效率降低甚至出现叶片与静子碰磨的情况,应优先考虑做好第4 级轮盘的平衡工作。
2)无论是一阶还是二阶临界转速,转子的不平衡响应对1 号轮盘的不平衡量均不敏感。可见,若压气机转子的第1 级轮盘存在叶片缺损,就动力学而言,对于压气机的稳定运行不会带来过大影响。
3)在二阶临界转速下,4 号轮盘上特征位置的不平衡响应对取定的所有5 个位置上的不平衡量均不敏感,这一点从响应曲线中也有很直观的体现。由表3 还可看出,3 个特征位置的二阶不平衡响应均对4 号轮盘上的不平衡量不敏感。由于转子不会越过一阶临界转速,因而此处的分析仅具有理论意义,不进行更细致的分析。
4 结 语
转子结构动力学的数值仿真表明:
1)低压压气机转子前2 阶弯曲模态频率分别为189 Hz 和505 Hz,整体盘鼓式结构设计给转子带来较好的刚度特性。
2)一阶临界转速为12 825 r/min,工作转速相对于临界转速有充分的裕度,结合1)的结果可知燃机在全工况区域内运行不会产生较大挠度,对于压气机运行的稳定以及可靠的工作效率具有重要意义。
3)压气机的设计和制造过程中重点对转子第4级给予重视,做好第4 级的平衡工作,并且保证此处材料及工艺以满足结构的强度要求。
[1]孟光.转子动力学研究的回顾与展望[J].振动工程学报,2002,15(1):5-13.
MENG Guang.Retrospect and prospect to the research on rotordynamics[J].Journal of Vibration Engineering,2002,15(1):5-13.
[2]刘延柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998.
[3]康召辉,任兴民,刘婷婷.一种轴型盘转子系统临界转速的计算分析[J].机械科学与技术,2008,27(10):1177-1180.
KANG Zhao-hui,REN Xing-min,LIU Ting-ting.Calculation and analyse of the critical speeds of a rotor system with great thickness[J].Mechanical Science and Technology for Aerospace Engineering,2008,27(10):1177-1180.
[4]关琦,等.某型燃气轮机低压涡轮压气机转子动力学分析[J].舰船科学技术,2010,32(8):127-132.
GUAN Qi,et al.Analysis on rotordynamic of the low turbocompressor[J].Ship Science and Technology,2010,32(8):127-132.
[5]宋兆泓,熊昌炳,郑光华.航空燃气涡轮发动机强度设计[M].北京:北京航空学院出版社,1988.
[6]顾家柳,等.转子动力学[M].北京:国防工业出版社,1985.
[7]佟德纯.工程信号处理及应用[M].上海:上海交通大学出版社,1989.
[8]曾攀,等.基于ANSYS 平台有限元分析手册——结构的建模与分析[M].北京:机械工业出版社,2011.
[9]付才高,郑大平,欧园霞,等.转子动力学及整机振动(航空发动机设计手册第19 册)[Z].北京:航空工业出版社,2000.
