关于高职数学函数连续性的教学

于洁

（山东药品食品职业学院 山东 威海 264210）

关于高职数学函数连续性的教学

于洁

（山东药品食品职业学院 山东 威海 264210）

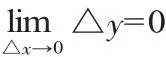
高职数学；函数连续性；连续本质；研究方法

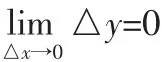
究其原因有以下几点；一是学生抽象概括能力欠缺。从客观世界的现实中抽象概括出数学概念，对接受过高中教育的人而言，应该初步具备了这种能力。但目前高职学生这方面能力普遍较差。二是学生对极限思想和方法的不适应。由于高等数学是建构在极限理论的基础上、以极限为基本工具研究函数的一门数学学科，因此，研究问题的思维方式总体上由“静态”变成了“动态”。而函数的连续性是运用极限理论定义的第一个概念，学生对于运用极限思想刻画函数的这种动态特性，需要一个适应过程。三是教材的简化。现在选用的高职高专《高等数学》规划教材，在“必需、够用”原则的指导下，降低了理论难度、简化了知识内容。多数教材的“函数连续性”一节直接给出函数在点连续的定义，缺少必要的例证加以辅助。学生很难通过阅读教材理解函数连续的概念。针对上述原因，教师在教学时应着重抓住以下几点，帮助学生建立起函数连续性的概念。

函数连续性的本质特征

要理解函数连续的概念，首先要抓住连续的本质特征。自然界中植物的生长、河水的流动、温度的变化等等现象，都是连续变化着的，把这种现象进行抽象，反映在函数关系上就是函数的连续性。如果只是这样概括，学生对连续本质特征的把握是不到位的。此时可再从以下现象分析：两个人几天不见，再次见面时并没有感觉到彼此的变化，难道这几天俩人真是都没有变化吗？显然不是。人从出生到衰亡，时时刻刻都处在连续变化之中，尽管这种变化很微小，不宜察觉，但它是不间断的。如果我们从函数的角度分析，上述现象就相当于函数的自变量在某一区间段上连续变化时，因变量也随之连续变化，即使自变量的变化很微小，因变量也会随之有微小的变化。经过的这样分析，学生就能较好地把握函数连续性的本质特征了。

函数连续性的研究方法

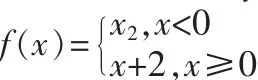
用什么方法确定函数在一点上的连续呢？函数在一点上的连续是一个局部概念，反映了函数在一点处两个变量增量间的变化关系，即当函数的自变量有一微小变化时，因变量也随之有一微小变化。如果利用初等数学的方法刻画这种关系，显然是行不通的，只有借助于极限工具进行深入的分析研究。通过教师适当引导，学生便会知道要想解决函数在一点上的连续的问题必须运用极限的思想方法。

函数连续性的定义

一个数学概念的形成过程，是人们对客观现象进行探索归纳、抽象概括的过程。教学上如果对这一过程进行情境再现，不仅可以使学生了解概念的形成背景，而且对学生理解掌握概念的本质及其应用大有益处。若只是“填鸭式”传授，把概念直接灌输给学生，效果可想而知，也失去了通过数学教学过程对学生进行观察分析、抽象概括能力培养的作用。

讲授“函数连续性”一节时，可以先借助多媒体给学生播放植物的生长、河水的流动、汽车在高速路上奔跑等连续现象，再播放一棵大树被拦腰截断、一条大坝截住河水流动、一座断裂的桥梁造成车辆停滞不前等不连续现象，与学生一起分析探索上述现象引出函数连续尤其是在一点上的连续的问题，并形成定义。

通常，关于函数y=f（x）在点x0连续的定义有两种形式：

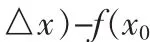
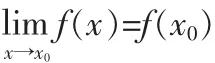
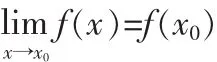
若先讲定义2可以列举以下实例：

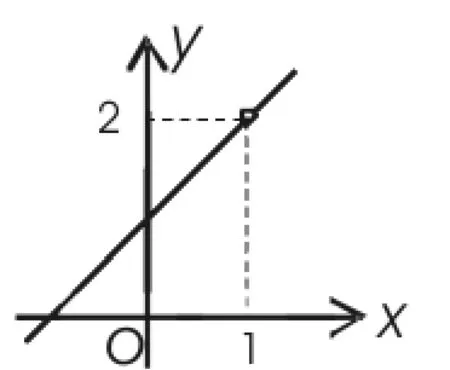
图1

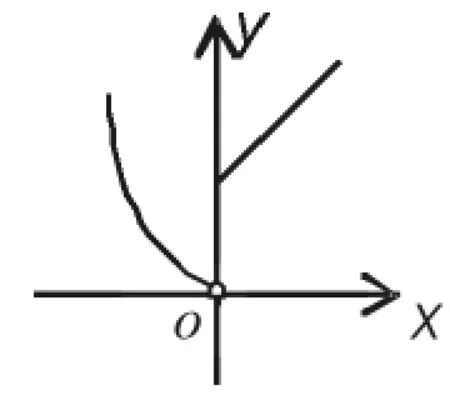
图2

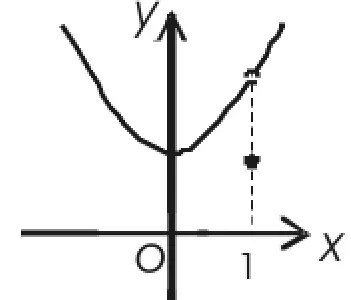
图3

三例过后进行小结，得出函数y=f（x）在点x0处若遇到下列三种情况之一就会不连续：（1）没有定义；（2）有定义、极限不存在；（3）有定义、极限存在、但极限值与函数值不相等。这时善于思考的学生就会产生下列想法：“当函数y=f（x）在点x0处同时满足了有定义、极限存在、极限值与函数值相等三个条件时，情况会是怎样呢？”这时教师可以引导学生观察连续函数曲线在一点上的状况。

例4：考察函数y=x2在点x=2处的连续情况。

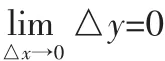
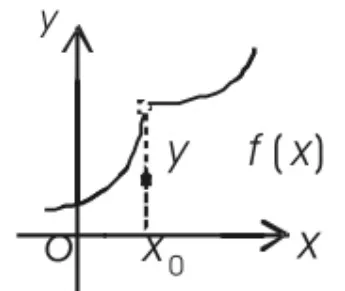
图4

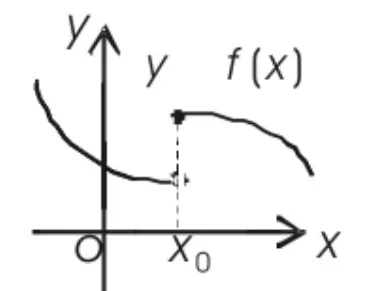
图5

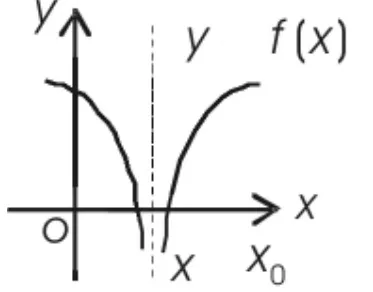
图6

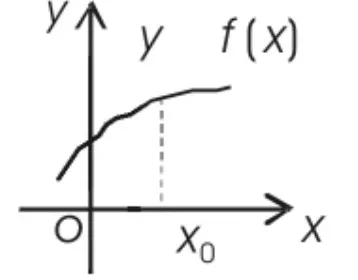
图7

函数连续性的整体概念

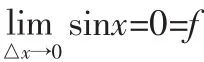
一般的，知道了怎样判定函数在一点上连续后，应给出函数在开区间（a，b）上连续的概念，即在开区间（a，b）内连续的函数y=f（x），必须在开区间（a，b）内每一点都连续。根据上述要求，在探讨函数y=sinx在（-∞，+∞）上连续的问题时，要说明y=sinx在（-∞，+∞）内的“每一点”都连续，显然逐点验证是不可能的，如果能够寻找到可以“代表”每一点的“点”，通过证明函数在此点连续，进而就可说明函数在区间上连续。

经分析发现，只要在区间（-∞，+∞）上设出任意一点，用“任一点”代替“每一点”加以证明即可使问题得到解决，这也正是数学简约美之所在。如果考察函数y=f（x）在闭区间[a，b]上的连续性，不仅要求它在区间（a，b）上连续，而且还要满足在区间的左端点a处右连续，右端点b处左连续。至此，关于函数连续性的概念就完整了，学生就会达成这样的共识：函数的连续是动态变化的，是通过函数在其定义区间上的每个点上的连续实现的。连续函数的图形呈现为一条连绵不断的曲线。

[1]曹之江.谈数学及其优教（名师谈数学）[M].北京：高等教育出版社，2008.

[2]罗韵蓉.浅谈函数的连续性与间断点的教学体会[J].科学咨询，2009，（4）.

[3]张景中.数学与哲学[M].大连：大连理工大学出版社，2008.

[4]同济大学应用数学系.高等数学[M].北京：高等教育出版社，2007.

[5]盛祥耀.高等数学[M].北京：高等教育出版社，2008.

于洁（1963—），女，山东宁津人，山东药品食品职业学院副教授，研究方向为高等数学教育与素质教育。

（本文责任编辑：谢良才）

□有话职说

走正直诚实的生活道路，必定会有一个问心无愧的归宿。

——高尔基

G712

A

1672-5727（2012）04-0114-02