对中职学生数学解题反思能力的培养

李碧璀

（厦门工商旅游学校 福建 厦门 361012）

对中职学生数学解题反思能力的培养

李碧璀

（厦门工商旅游学校 福建 厦门 361012）

举例阐述了中职数学教学实践中，如何在数学解题上采用由易到难，由基础到深入的方法，对中职学生在数学解题反思方法上进行引导，逐步培养中职学生的数学解题反思能力，从而提高中职学生的数学能力。

中职学生；数学解题；反思能力；培养

自古以来，我国教育家就强调反思意识，“学而不思则罔，思而不学则殆”，“吾日三省吾身”等至理名言就是印证，他们强调学与思的统一，注重学习后的反思。数学解题中的反思，特指学生在练习过程中适时回望学习经历、及时修正解题策略、监控调节解题过程的思维过程，其最终目的是促进学习目标的有效达成。数学解题反思是提高解题能力的一个重要环节，解题反思贯穿解题学习的全过程，也是对解题的元认知过程。在实际解题过程中，由于学生的数学认知结构水平的限制及非认知因素的影响，学生往往表现出对基础知识不求甚解，不善于对自己的思考过程进行反思，缺乏解题后对解题方法、解题中反映出的数学思维方法、特殊问题所包含的一般意义的概括，导致获得的知识系统性弱、结构性差。尤其是中职生，他们对数学的兴趣不大，基础相对薄弱，做题相当被动，让学生在解题过程中养成解题反思习惯，从而提高数学能力，有很重大的意义。

培养学生的反思意识

态度是做好一切事情的前提，是成功的基础。因此，在培养学生解题反思习惯时，首先应着重培养学生的反思态度、反思意识。多数中职生的学习习惯不是很好，他们往往不愿花太多时间在学习上；但是他们尚能意识到数学作为一门基础学科的重要性。所以，在一开始，可以把解题反思的重要性和必要性告诉学生，先使他们的思想中有反思意识，然后再由易到难，就审题、解题过程、解题后如何进行反思对学生进行方法上的引导，使他们逐步养成习惯。

在教学实践中，很多中职生往往是看到数学题后根本不知道从何下手，哪怕最简单的题目。因此，在一开始，可以通过波利亚的“怎样解题”四步骤来进行解题任务分解，通过任务驱动引导学生进行解题反思。

例1：已知等差数列的第6项是5，第3项与第8项的和也是5，求这个等差数列前9项的和。

步骤二：拟定计划。问题3：怎样求解本题？通过对题目的分析，要求出Sn需要先求出a1，再根据解题需要求出d或者an。显然本题要求出an也需先求出d，所以，为了简化步骤就选择公式（2）。

步骤三：实现计划。用通项公式an=a1+（n-1）d求出a1和d。师：“本题的a1和d能直接求出来吗？”生：“不能”。师：“该怎么办？”生：“要列方程”。师：“对。怎样列？”生1：“根据已知条件中a6=a1+（6-1）d列出第一个方程；再根据已知条件中a3+a8=a1+（3-1）d+a1+（8-1）d列出第二个方程。连立方程组。”生2：“或者把第一个方程中的a1用d表示代入第二个方程。”师：“对。然后呢？”生：“把所求出的a1和d，n=9代如公式（2）既可求解。”

步骤四：回顾。（1）正面检验每一步，推理是有效的，演算是准确的。（2）回顾这个解题过程可以看到，解题首先要弄清题意，同时又要及时提取记忆网络中的有关信息。这当中，起调控作用的关键是构思出一个成功的计划（包括解题策略）。（3）在心理机制上，这个案例呈现出“激活——扩散”的基本过程，激活了记忆网络中的解题方法，然后根据各种方法的适用条件选定本题的解法。在本题的教学中，应先让学生思考该用什么数学知识、方法解决问题，通过帮助学生整理思维过程，反思解题过程中数学公式之间的联系，促进解题思维常规化，从而才有可能反思数学思维过程，优化解题思路，让学生经过思考与探索，促进反思，提高反思能力。

提高学生的综合解题能力

在学生学会了初步的反思方法之后，可以进一步要求学生积极反思，探求一题多解，提高综合解题能力。

一个数学问题，由于审视的角度不同，往往会得到多种不同的解题方法。在教学中，教师在学生掌握基本解法的基础上，应鼓励学生去反思，去探讨和寻求更好、更简捷的解法，使学生通过反思，学会从不同角度、不同方位去审视、去思考，从而沟通知识间的纵横联系，训练和培养学生的发散思维能力。众所周知，数学知识有机联系纵横交错，解题思路灵活多变，解题方法途径繁多，但最终却能殊途同归。即使一次性解题合理正确，也未必能保证一次性解题就是最佳思路、最优最简捷的解法，不能解完题就罢手。

例2：已知三点A（1，2），B（3，3），C（7，5），求证：A、B、C三点共线。

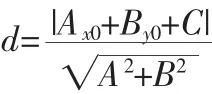
对知识点做横向与纵向比较

很多学生做题易就事论事，就题论题，不能通过反思对各知识点进行比较、小结，从而将知识有机地联系起来，形成有效的知识网络，导致掌握的知识支离破碎，容易遗忘。

例3：判断下列5个命题中正确的命题是____：（1）若y=f（x）为偶函数，则y=f（x+2）的图像关于直线对称x=2；（2）若y=f（x+2）为偶函数，则y=f（x）的图像关于直线x=2对称；（3）若f（x-2）=f（2-x），则y=f（x）的图像关于直线x=2对称；（4）若f（x+ 2）=-f（-x)，则y=f（x）的图像关于点（2，0）对称；（5）函数y=f（x-2）与y=f（2-x）的图像关于直线x=2对称。

这个问题的正确答案是（2）和（5）。这道题目需要我们反思所有与函数相关的对称性知识点，并通过对这5个命题做横向比较，弄清函数的对称问题。比较（1）、（2），我们要弄清的问题是：偶函数关于y轴对称，所以，倘若y=f（x）为偶函数，则y=f（x+2）是由y=f（x）向左平移2个单位得到，所以y=f（x+2）的图像关于直线x=-2对称；倘若y=f（x+2）为偶函数，则y=f（x）是由y=f（x+2）向右平移2个单位得到，所以y=f（x）的图像关于直线x=2对称。比较（3）、（4），我们要弄清的是关于函数自身的对称问题的两个重要结论，结论1：函数y=f（x）关于直线x=a对称的充要条件是：对定义域内的任意x都满足f（a+ x）=f（a-x），即f（x）=f（2a-x）。结论2：函数y=f（x）关于点（a，b）对称的充要条件是：对定义域内的任意x都满足f（a+x）+f（ax）=2b，即f（x）+f（2a-x）=2b。所以，若f（x-2）=f（2-x），则y=f（x）的图像关于直线x=0对称；若f（x+2）=-f（-x），则y=f（x）的图像关于点（1，0）对称。比较（3）、（5），我们要弄清函数的对称分为：函数自身的对称性与两个不同函数的对称性。所以对于命题（5），就不能套用上述关于函数自身对称问题的那两个结论。首先，我们知道y=f（x）与y=f（-x）是关于x=0对称，而y=f（x-2）和y=f（2-x）分别是由y=f（x）和y=f（-x）向右平移两个单位得到，所以函数y=f（x-2）与y=f（2-x）的图像关于直线x=2对称。

经常对做过的题目做这样纵向或者横向的知识反思和比较，做归纳与总结，可以让学生对自己学过的内容有较系统的认识，从而达到会做一题就会做百题的效果。

总结

综上所述，可归纳总结解题反思的步骤如下：一是进行审题反思，就是应该反思如何审题。这里要指出的是，反思不一定在解题之后，也可以在解题之前或解题之中，在遇到一个新颖的题目时，我们应该要搞清未知数是什么，已知数据是什么，条件是什么，要确定未知数，条件是否充分，把条件的各个部分分开来分析，甚至可以画图引入适当的符号。这样可以给我们提供一个数学建模的模式，也有利于我们分析题目。二是反思解法，拟定计划。反思以前是否见过这个题目，是否见过相同的问题只是形式不同而已，以及是否知道与此类问题有关的公式或者定理。三是反思计划，叙述解法。数学是培养逻辑思维的，所以我们要注意反思，这样才能让我们的数学能力有质的提高。四是查漏补缺，反思解题过程，总结解题经验。要思考：对你的求解过程自己检验过吗？你能否用别的方法来解这个题目？你用的这个方法或结果能否用于解决其他问题？五是反思基本的解题模式，做到举一反三。要在解题中抽象出基本的解题模式，并系统小结，对知识点做横向与纵向的比较，形成牢固的知识体系。

我校通过对学生数学解题反思能力的培养，增强了学生数学解题的自觉性、主动性，促进了学生良好解题反思习惯、反思意识的形成，同时增强了学生学习数学的兴趣。学生发现，很多问题只要联系所学知识自己都能解决，而且通过自己的思考，对于做错的地方也更能理解。养成良好的解题反思习惯后，学生学习数学的积极性有了很大提高，学习兴趣也浓厚了。教师都是引导学生如何去发现问题、解决问题，而不是一味灌输，使学生懂得了要经历“感知——领悟——运用”的学习过程。

引导学生解题反思能优化学生思维，促进学生的思维升华到一个更高的水平，使学生获得深入学习所必需的思维品质，真正体现“以学生发展为本”的教育理念。总之，培养学生数学解题的反思能力，不仅可以提高学生的数学素质，培养学生的数学意识，更可以促进学生思维能力的发展，为学生获得终身受用的基础能力和创造才能奠定基础。

[1]张定强，赵宏渊.论数学反思能力[J].课程·教材·教法，2005，25（3）：49-54.

[2]曹一鸣，王仲英.略论数学反思能力的培养[J].中学数学教学参考，2004，（9）：1-2.

[3]王家聪.新课程理念的实施需要学生反思能力的培养[J].数学教学通讯，2004，（2）.

[4]段训明.增强反思意识 优化思维品质[J].数学通报，2003，（6）.

[5]薛党鹏.解题回顾与数学思维品质的培养[J].数学通报，1999，（12）.

李碧璀（1968—），女，福建厦门人，硕士，厦门工商旅游学校讲师，研究方向为课程。

（本文责任编辑：谢良才）

G712

A

1672-5727（2012）04-0103-02