仿真得出的隐身飞机短波波段雷达截面积特性

王 凯，王建路，韩国玺，傅从义

（解放军电子工程学院，安徽 合肥 230037）

0 引言

天波超视距雷达（OTHR）工作在短波波段（5～30MHz），它利用电磁波在电离层与地面之间的反射作用传输高频能量，自上而下探测超远距离空中和海上运动目标，其作用距离不受地球曲率限制［1］。

雷达散射截面积（RCS）是分析天波雷达探测效能的一个必不可少的参数，隐身飞机就是通过减小RCS来降低敌方雷达作用距离的，从而达到提高突防概率和生存能力的目的。传统的微波视距雷达的目标RCS特性处于光学区，而短波电磁波从飞机的脊背照射，波长和目标尺寸是可比拟的，处于谐振区［2］。这一情况使得适用于简单目标特性分析的绕射理论的渐近方法和几何光学等解析方法不再适用。天波超视距雷达探测F－22隐身飞机时，RCS值随着工作频率、极化和入射方向的变化规律目前研究的并不多，并且得不到F－22短波波段的RCS实测值。为研究天波超视距雷达探测隐身飞机的能力，有必要采用仿真的方法来推测其RCS。

1 XFDTD软件与3ds－Max模型

1.1 XFDTD软件

时域有限差分法（finite－difference time－domain method，FDTD）是一种直接求解Maxwell旋度方程的电磁场值数值分析方法。XFDTD是基于时域有限差分法（FDTD）的全波三维电磁仿真工具，广泛应用于天线、射频／微波、电磁兼容、电磁散射计算和光学等领域［3］。XFDTD计算电磁散射时，首先利用FDTD算法计算出紧邻目标的近场电磁场，通过近－远场变换得到远场的结果，具体方法见文献［3］。然后通过Fourier变换转换到频域，根据RCS的定义：

即可求出最终结果。利用XFDTD进行雷达目标RCS仿真计算，需要进行3个步骤：

1）散射目标的几何建模和FDTD网格剖分，网格单元的边长通常小于入射波上限频率的1／10波长。

2）定义激励源和仿真计算参数。

3）选择所需的结果运行计算。

1.2 3ds－Max模型

对散射体进行计算，必须要能够准确地描述该散射体的外形。3ds－Max是AutoDesk公司推出的在微机上应用的具有突破性的造型、渲染和动画的CAD软件。3ds－Max可以快速、精确地完成复杂目标的实体建模，能够严格地描述目标的几何尺寸和物理参数，目前已广泛应用于机械制造、建筑设计和军事仿真领域。在飞行员训练中，已经在计算机上广泛使用3ds－Max及其模型模拟真实飞行情况，使飞行员身临其境［4］。文献［5］利用3ds－Max建立预警机模型，并对其RCS进行了分析。本文采用F－22 3ds－Max模型完全按照真实尺寸同比例建模，模型的准确性是可靠的。

1.3 F－22短波段RCS仿真

利用3ds－Max强大的建模功能，建立F－22目标3ds－Max模型，建模数据为F－22机身总长18.89m，翼展13.56m，全高5.08m，为依据F－22战机实际尺寸而建立的3ds－Max模型三维图，见图1。然后利用3ds－Max自身的导出功能导出三角面片数据文件，并进行FDTD网格离散，最后拼装为复杂整体离散模型。图2为F－22飞机的离散结果图。

图1 F－22战机的三维图Fig.1 Three dimension of F－22

图2 F－22战斗机离散模型的俯视平面Fig.2 Top view of F－22discrete model

根据天波超视距雷达短波电波通过电离层折射下视探测目标的机理，建立以目标为基准的极坐标系。见图3。图3中，xOy所在平面是飞机俯视平面，φ是偏离x轴正方向的水平方位角，θ为偏离z轴正方向的仰角。φ＝0°时为从飞机头部入射，φ＝180°时为飞机尾部入射。

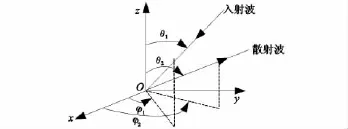
图3 以目标为基准的极坐标系Fig.3 Polar coordinates based on target

F－22主要通过外形设计和涂覆吸波材料来实现RCS的缩减。根据吸波材料的涂层厚度要达到波长的1／4的要求，材料隐身在短波波段已经失去了作用，这里只考虑飞机外形和体积对RCS的影响。计算时取F－2 2机身材质为金属，电参数为：εr＝1.0，σ＝3.72×107S／m，μr＝1.0，σm＝0.0。设置离散立方体网格边长尺寸为δ＝0.36m。入射高斯脉冲如式可以表示为：

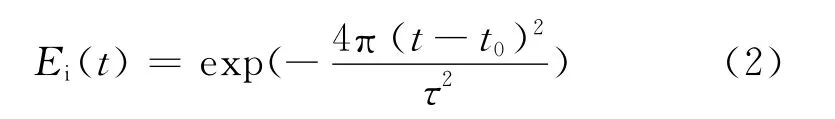
式中，时间步长为Δt＝δ／2c，其频率上限为83.28 MHz，在以下条件下对该型战斗机的后向RCS进行了仿真计算：

1）5～30MHz的HH极化和VV极化（平面波发射和散射接收均为水平极化或垂直极化）；2）入射波俯视角（即入射射线与机身水平面的夹角）从0°～30°，对应极坐标系，θ分别为100°、110°、120°和130°；3）入射波水平方位角（即入射射线在水平面投影与飞机机身纵轴法线的夹角）从0°～60°，间隔为10°。

2 仿真结果

1）入射波方位角φ从0°到30°，θ从100°～130°，HH极化时短波波段内RCS的变化，见图4。2）入射波俯视角固定20°即θ为110°，φ从10°变化到30°，HH和VV极化时短波波段内RCS的变化，见图5。3）θ固定为110°，φ从40°变化到60°，HH 极化和VV极化时RCS在短波波段内的变化，见图6。

图4 φ＝0°～30°，θ从100°变化到130°HH极化RCS随频率变化Fig.4 RCS versus frequency in HH polarization withφfrom 0°to 30°andθfrom 0°to 130°

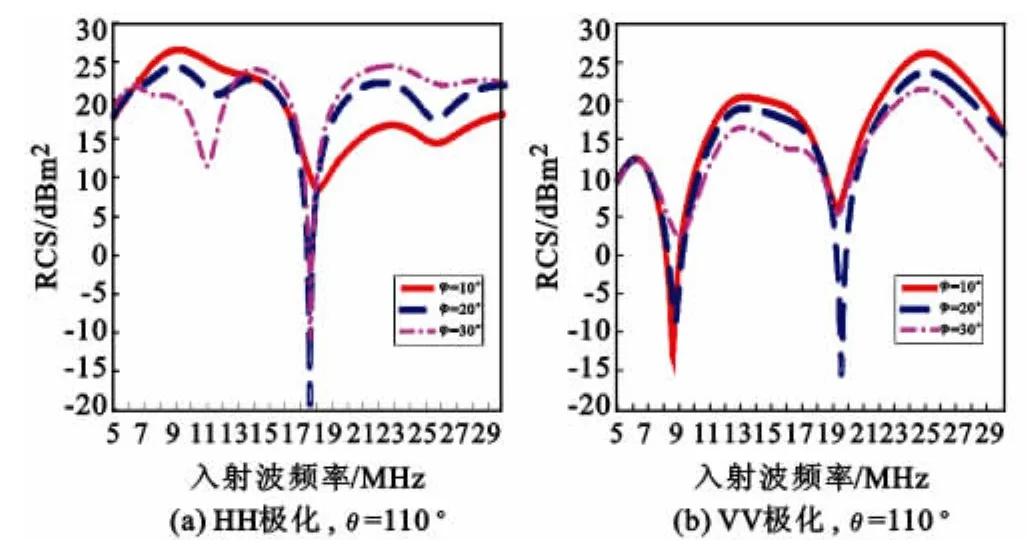
图5 短波频段HH极化和VV极化，θ＝110°，φ从10°～30°时RCS幅度变化Fig.5 RCS versus frequency in HH or VV polarization withθ＝110°andφfrom 10°to 30°

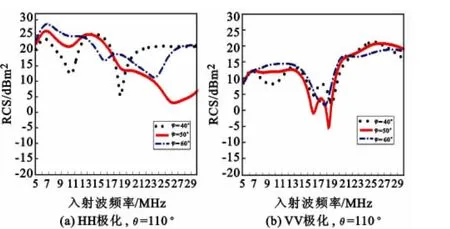
图6 短波频段HH极化和VV极化，θ＝110°，φ从40°～60°时RCS幅度变化Fig.6 RCS versus frequency in HH or VV polarization withθ＝110°andφfrom 40°to 60°

3 结果分析

3.1 金属球体的验证对比

为说明仿真结果的可信性，以金属球为例来加以说明。金属球体的平面波散射问题从Maxwell电磁方程开始，根据波动方程和边界条件可以严格地获得散射场的精确解即它的 Mie级数解［6－7］。设金属球半径为1m，FDTD元胞为δ＝0.05m，时间步长为Δt＝δ／2c，离散后的球半径为20δ，则其频率上限600MHz，入射平面波采用高斯脉冲如式（2）所示。其中τ＝32Δt为脉宽，时间步设为2 000步，沿z轴入射。文献［8］给出了同样条件下的FDTD算法仿真和Mie级数的精确解的宽带后向散射特性，见图7（a）。XFDTD的仿真结果见图7（b），仿真结果与Mie级数解吻合的很好。因此，利用XFDTD软件计算RCS得到的结果是可靠的。

3.2 F－22RCS仿真结果分析

图4（a）—图4（d）所示为从飞机鼻锥方向（±30°），不同俯仰角情况下，RCS随频率变化的一系列图。总体上看，HH极化时，当水平方位角分别固定以后，短波波段的目标RCS特性受入射波俯仰角θ变化的影响不是太大，在低频段曲线几乎是重合的，并且在大部分频率区间战斗机鼻锥方向的RCS值在15dBm2以上。随着方位角偏离加大，RCS波动变大。

图7 金属球远区后向散射Fig.7 Far zone backscatter of metal sphere

如图5（a）所示，入射波俯仰角固定为110°（即入射射线与水平面的夹角为20°），水平方位角从±10°变化到±30°（即从战斗机鼻锥方向照射）时的HH极化（水平极化发射，水平极化接收）时的单站RCS的估计值在短波波段5～30MHz内随频率变化的幅度曲线。图5（b）为VV极化时对应的变化曲线。可以看出，HH极化时，在5～16MHz和18.5～30MHz时频率范围内的后向RCS值为10～26dBm2（10～398m2）。其中在f≈9MHz附近出现第一个峰值点20～25dBm2，在f≈14MHz附近出现第二峰值点，在14MHz＜f＜18MHz区间RCS随频率增加而减小，18MHz＜f＜30MHz区间RCS随频率增加而增加。在f≈23MHz附近出现第三个峰值点。从总体上看，在5～20MHz区间，HH极化时的RCS大于VV极化时的RCS。

如图6（a）所示，HH极化时入射波俯仰角固定为110°（即入射射线与水平面的夹角为20°），在与机身法向方位夹角±40°～±60°范围内的单站RCS随频率的变化，图6（b）为VV极化时对应的曲线。HH极化时在5～17.5MHz范围内RCS在10～30dBm2（10～1 000m2）内，第一个峰值点出现在7 MHz附近，而在9MHz却出低谷；第二个峰值点出现在15MHz附近，并且在12～17MHz范围内保持在20～25dBm2之间。总的来说，VV极化时的RCS整体上要比HH极化时的要小，只有在20 MHz以后RCS才随频率增加呈现递增趋势并且不超过20dBm2。

4 结论

本文采用成熟的XFDTD电磁计算软件结合3ds－Max模型，对F－22短波波段的后向散射RCS特性进行了仿真。仿真得出：F－22在短波波段散射特性接近谐振散射，RCS值较大，并且随着入射雷达频率和入射角度的改变会进一步增大。分析表明：这些特性导致隐身飞机在短波波段很难隐身，与报道的天波雷达可以探测F－22相吻合，并为天波雷达的参数设计及使用方法指出了方向。

［1］刘慧霞，梁彦，程咏梅，等.天波超视距雷达的坐标变换［J］.计算机仿真，2006（3）：70－74.LIU Huixia，LIANG Yan，CHENG Yongmei，et al.A coordinate transformation algorithm for over the horizonradar［J］.Computer Simulation，2006（3）：70－74.

［2］黄培康，殷红成，许小剑.雷达目标特性［M］.北京：电子工业出版社，2005.

［3］庄钊文，袁乃昌，莫锦军，等.军用目标雷达散射截面预估与测量［M］.北京：科学出版社，2007.

［4］碧峰.中文3DMAX教程［M］.珠海：珠海出版社，2001.

［5］张世田，任小红，杨利霞，等.一种基于FDTD的目标双站 RCS计算方法及其应用［J］.微波学报，2011（3）：5－8.ZHANG Shitian，REN Xiaohong，YANG Lixia，GE Debiao.A novel method of object bistatic RCS based on FDTD method and its application［J］.Journal of Microwaves，2011（3）：5－8.

［6］王海龙，吴群，吴健，等.一种高效的计算 Mie级数的新方法［J］.电波科学学报，2006（6）：811－814.WANG Hailong，WU Qun，WU Jian，et al.A new and highly effective approach for calculating the Mie series［J］.Chinese Journal of Radio Science，2006（6）：811－814.

［7］王茂琰，徐军，吴健，等.基于 Mie级数的金属球被双负介质覆盖的电磁散射［J］.系统工程与电子技术，2008（8）：2 083－2 086.WANG Maoyan，XU Jun，WU Jian，et al.Electromagnetic scattering of metallic sphere covered by double－negative metamaterials based on Mie series［J］.Systems Engineering and Electronics，2008（8）：2 083－2 086.

［8］葛德彪，闫玉波.电磁波时域有限差分方法［M］.西安：西安电子科技大学出版社，2005.