单调算子的不动点定理研究

金朝钧

(鸡西大学，黑龙江 鸡西 158100)

单调算子的不动点定理研究

金朝钧

(鸡西大学，黑龙江 鸡西 158100)

单调算子广泛存在于非线性微分方程和积分方程的研究中，拟给出非紧非连续的单调算子的一条不动点定理。

单调算子；不动点

1引言和预备

单调算子广泛存在于非线性微分方程和积分方程的研究中，本文给出非紧非连续的不动点定理。

以下均设E是实Banach空间，θ是E中的零元，P是E的锥，≤是由P定义的半序，即∀x，y ∈E ，若y-x ∈P，则x≤y. 锥P称为正规锥，若果存在常数M0，使得θ≤x≤y(x，y ∈E)蕴含‖x‖≤M，‖y‖，其中M为正规常数。锥称为体锥，如果P中含有内点A()→∠φψ.

设D⊂E.A:D×D→称为混合单调算子，如果A(x，y)关于x单调递增，关于y单调递减，x*∈D称为不动点。如果A满足A(x*，x*)=x*.设hθ,记hθ={x∈E:∃λ，μ0，λh≤μh}. 显然，若P是体锥设eθ成A：P→E为e-凹算子，若：

(i) AA(P-{ϑ})⊂Pe；

(ii)∀x∈Pe∀0t1,∃η=η(t,x)0，使得

A(tx)≥(1+η)tAx

(1.1)

成立，η=η(t,x)称为A的特征函数

A(tx+(1-ty))≤tAx+(1-t)Ay

(1.2)

A称为凹算子，若-A是凸算子

A(tx)≥tαAx(A(tx)≤t-αAx),

∀x∈D,t∈(01).

(1.3)

定义 设D⊂E,A:D×D→E,fg-凹凸算子，若存在f :(0,1]×D→(0,∞)以及

(1)A(tx,y)≥f (t,x)A(x,y),∀t∈(0,1),(x,y)∈D×D;

2主要结果与证明

命题 设P是E中的正规锥，u0,v0∈E,u0≤v0,A:[u0,v0]×[u0,v0]→E是混合算子，若A是fg-凹凸算子，且满足

(1)∃r0u0u0≥r0v0;v0≤A(u0,v0),A(v0,u0)≤v0；

(2)∃ω0∈[u0,v0]f (t,x)g(t,x)((tx)∈(0,1)×[u0,v0])关于x在ω0取得最小值，且f；g关于t下半连续，则A在[u0,v0]有唯一不动点。

定理 设P是E中的正规锥，A:P×P→E是混合算子，且满足

(i)对固定y,A(·，y):P→E是α凹算子，对固定的x，是A(x,·)：→E凸子

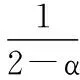
A(u0,v0)≥εA(v0,θ)

(2.1)

则算子A在[u0,v0]中有不动点

证明 令uun=A(un-1,vn-1)，vn=A(vn-1,un-1),n=1,2,…,知

u1≤A(u1,v1),A(v1,u1)≤v1

以及

u0≤u1≤u2…≤un≤…≤vn…≤v2≤v1≤v0

由(2.1)得

u1≥εv1,

于是ε∈(0,1],往证A:[u1,v1]×[u1,v1]→E是fg-凹凸算子，只需证A:[u0,v0]×[u0,v0]→E 是fg-凹凸算子，其中

(2.2)

事实上，∀x,y∈[u0,v0],t∈(0,1)，有

A(x,ty)=A(x,ty+(1-t)θ≤tA(x,y)+(1-t)A(x,θ)

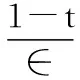
A(tx,y)≥tαA(x,y)=f (t,x)A(x,y)

下证f与g满足

(2.3)

(2.4)

知(2.3)等价于

(2.5)

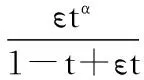
再由

φ(t)=εtα-1=(1-ε)t-1

(2.6)

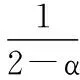
于是(2.5)式成立，得(2.3)式成立，故A:[u1,v1]×[u1,v1]→E是fg-凹凸算子。再由(2.4)式知关于x单调，关于t下半连续，由命题知A在[u1,v1]中有唯一不动点，从而A在[u0,v0]有唯一不动点。

[1]金朝钧，等.非线性分析引论[M].哈尔滨；东北林业大学出版社,2004.

[2]金朝钧.序集原理与不动点定理[J].哈尔滨师范大学自然科学学报,2004(4).

[3]金朝钧.增集值映象不动点定理[J].鸡西大学学报,2006(5).

[4]姜丽娟,金朝钧.集值映象不动点定理[J].哈尔滨师范大学自然科学学报,2006(4).

[5]孙经先.非线性泛函分析序集一般原理的推广[J].系统科学与数学,1990(3).

[6]张金清,等.一个非线性连续增算子不动点定理及应用[J].应用数学学报,2001(1).

[7]孙经先.凸幂 凝聚算子的不动点定理及其对抽象半线性发展方程的应用[J].数学学报,2005.

[8]周英告.多值增算5一个子的不动点定理[J].应用泛函分析学报,2006(6).

[9]杨云苏.Banach 空间中定点非扩张随机半闭1- 集压缩映象的随机不动点定理[J].工程数学学报,2006(8).

ClassNo.:O177DocumentMark：A

(责任编辑：郑英玲)

StudyofFixedPointTheoremofMonotoneOperator

Jin Chaojun

There are many monotone operators in the nonlinear differential and integral equations. This paper presents a fixed point theorem of the non-compact and non-continuous monotone operators.

fixed points；monotone operators

金朝钧，教授，鸡西大学。

黑龙江省教育厅科研项目(项目编号12515249)。

1672-6758(2012)12-0135-2

O177

A