由锐钛矿(101)片卷曲成单壁纳米管的紧束缚密度泛函理论研究

刘 昊 林梦海 谭 凯

(厦门大学化学化工学院,固体表面化学国家重点实验室,福建省理论与计算化学重点实验室,福建厦门361005)

由锐钛矿(101)片卷曲成单壁纳米管的紧束缚密度泛函理论研究

刘 昊 林梦海 谭 凯*

(厦门大学化学化工学院,固体表面化学国家重点实验室,福建省理论与计算化学重点实验室,福建厦门361005)

通过卷曲二维锐钛矿(101)周期性单层片(sheets)构造了一系列不同手性((n,0),(0,m),(n,m))的一维单壁TiO2纳米管.用周期性紧束缚密度泛函理论(DFTB)方法计算并比较了不同管径和手性的TiO2纳米管在几何结构、电子性质等方面的差别.结果表明:除了(6,0)管,其余纳米管随着管径的增大,应变能和能隙减小.而在管径相同的情况下,不同手性的(n,m)纳米管的应变能随着n/m的增加呈现先增大后减小的趋势,能隙变化不大.

紧束缚密度泛函理论方法;二氧化钛;锐钛矿;纳米管

1 引言

二氧化钛(TiO2)是一种重要的半导体过渡金属氧化物,在光催化、电子学、环境保护等领域中有着广泛的应用,对其性能及电子结构的研究是近年来热门的研究课题.1-13由于其具有量子尺寸效应、表面效应等性质,TiO2纳米材料(纳米薄膜、纳米线)在实际应用中具有巨大的价值.特别是TiO2纳米管的特殊结构,使它具有更大的比表面积和更强的吸附能力,表现出更高的光催化性能和光电转化效率,已经应用于光催化剂、太阳能电池、气敏传感材料、催化剂载体和超级电容器等领域.9,14-18目前TiO2纳米管的合成制备方法主要包括模板法、19水热法、6,15阳极氧化法16等.其中阳极氧化法适合大批量合成,并能通过控制电压等条件改变管体的形貌,而水热合成的纳米管管径最小,管壁最薄.

尽管已有大量实验工作的进展,但是TiO2纳米管形成机理和结构与性能的关系依然不清楚,开展相应的理论研究就显得非常必要.理论上单壁TiO2纳米管类似碳纳米管卷曲,可以视为不同晶型下具有二维周期性的片或层沿不同方向卷曲而成,用(n, m)两个参数就可以表示不同手性.对于金红石型(rutile)TiO2,He等20研究了不同晶面卷曲的纳米管,得到相关力学及电子性质.Meng等21从金红石(110)片出发,构造了不同结构的纳米管,利用密度泛函方法和分子动力学研究了它们的稳定性和性质.相对于金红石型TiO2,研究更多的是锐钛矿型(anatase) TiO2.Enyashin,22,23和Wang24等分别使用紧束缚(TB)、紧束缚密度泛函理论(DFTB)和密度泛函理论(DFT)方法对锐钛矿(110)六边形点阵的纳米管模型进行了计算,结果显示TiO2纳米管为半导体,其稳定性随半径增加而增加.从头算计算25结果显示,拥有直接能隙的TiO2(n,0)纳米管比拥有间接能隙的(0,m)在能量上更有优势,能隙随着半径减小而减小,在(n,0)纳米管的管径低于1.0 nm时,能隙发生骤然降低.Bandura和Evarestov26将锐钛矿(101)纳米管的结构进行了参数化,认为矩形晶格纳米管不存在n≠m≠0的情况,并用原子轨道线性组合(LCAO)方法计算比较得到半径相近的纳米管的结合能和能隙(n,0)＞(0,m)的结论.Hossain等27则研究了锐钛矿纳米管的电子性质以及光学各向异性.Evarestov等使用PBE0方法分别研究了单壁二氧化钛六边形点阵纳米管,28多壁二氧化钛六方点阵纳米管,29单层及多层二氧化钛矩形点阵纳米管30的对称性、能量和电子结构,结果显示,相同半径的矩形点阵的纳米管比六方点阵纳米管能量低,构型更稳定,多壁六方点阵纳米管比单壁的能隙大;对于矩形点阵二氧化钛纳米管而言,单壁6层纳米管比单壁12层纳米管的能量低.这与Ferrari等31的研究结果是一致的:在多种二氧化钛纳米管中,仅锐钛矿(101)纳米管的6层纳米管在应变能上优于更多层数的纳米管,由于管壁较薄,锐钛矿(101)单壁6层纳米管能达到更小的管径,实验合成最小的二氧化钛纳米管管径约为5 nm,锐钛矿(001)单壁3层纳米管在重构后相对于其它模型应变能有更大的优势,与实验相符得较好.

目前国内外的研究都局限于(n,0)和(0,m)两种构型纳米管,Ferrari等31在文献中提及锐钛矿(101) (n,m)(n=m)的构型,但是没有更进一步的探讨.本文将使用周期性模型对单层锐钛矿(101)纳米管多种手性的模型进行计算研究,讨论单壁锐钛矿(101)纳米管模型的手性结构与能量、成键以及电子性质的关系.

2 模型与计算方法

从锐钛矿晶体沿(101)面切割约为0.27 nm厚度的片,建立slab模型,真空层为1.0 nm,结构优化后的锐钛矿(101)纳米片如图1(a)所示.锐钛矿(101)纳米片为矩形点阵,相邻各边正交,边长分别为1.046和0.345 nm,在纳米片的二维结构中设置相互正交的单位向量a和b,其长度分别为矩形点阵的宽和长,a和b经线性组合得到手性矢量k=na+mb(n,m为非负整数),沿k方向进行卷曲得到相应(n,m)构型的纳米管,其管体横截面周长为|k|.

本文的计算工作均采用Materials Studio软件包中DFTB+模块.32为避免相邻管体之间发生相互作用,对每个单独的纳米管建立10 nm×10 nm×c nm的立方超晶胞,其中c为管长方向的晶胞参数.由于在所有晶胞参数中仅参数c对纳米管的几何结构有直接影响,为加快收敛速度,在进行晶胞参数优化时冻结除c外的所有晶胞参数.各种卷曲方式的纳米管重复单元的长度(即最小管长)不同,所以对c方向的k点进行了收敛性测试,并将(0,m)纳米管的k点设为1×1×8,其余纳米管均设为1×1×3.为比较不同管径纳米管的稳定性差异以及管体受到的应力影响,将应变能(Es)定义如下:

图1 几何优化后的锐钛矿(101)单层片(a)以及(21,0)(b,c), (0,7)(d,e),(7,7)(f,g)纳米管侧视及俯视图Fig.1 Side and top views of optimized anatase(101) single layer sheet and(21,0)(b,c),(0,7)(d,e), (7,7)(f,g)nanotubesSubscripts 2c and 3c express the coordination number of atom O, subscripts i and o indicate the inner and outer walls of nanotubes, respectively.

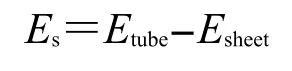
其中Etube为优化后的纳米管每个TiO2单位的平均能量,Esheet为优化后的纳米片每个TiO2单位的平均能量.

3 结果与讨论

表1给出了优化后的锐钛矿晶体与(101)纳米片晶胞参数、单位能量、能隙以及键长数据.与实验数据33相比,虽然PBE和DFTB方法均存在一定误差,但并不影响体系的本质性质,两种方法都能很好地模拟锐钛矿晶体和纳米片的几何结构,并提供定性描述.在锐钛矿晶体中仅存在两种Ti―O键长,在DFTB方法中计算得到的键长数据为0.206和0.203 nm,在纳米片中,由于Ti和部分O原子的配位数减少,Ti―O键分化为四种键长:0.211、0.199、0.198和0.190 nm.通过纳米片卷曲获得不同手性的单壁锐钛矿(101)纳米管:(n,0),(0,m)以及(n,m)(n,m≠0).(n, m)纳米管(n,m≠0)涵盖了除(n,0)和(0,m)构型外的所有手性纳米管,具体可分为n=m和n≠m两种类型,n与m的比值n/m决定了纳米管的手性,相同手性的纳米管在管径增加的时候n和m同比例增加,且n/m越接近1,管径变化步长越小.因此,我们选取了直径从1.0到4.5 nm的(n,0)纳米管(n=6+3i,i=0-10), (0,m)纳米管(m=4-12)以及(n,m)纳米管(n=m=4-12)作为讨论对象.所有纳米管均为六层结构,5配位的Ti原子分布在第三和第四层,O原子分为3配位和2配位两种配位形式,其中3配位的O原子在第二和第五层,2配位的桥O原子分布在纳米管最内和最外层.

图1给出优化后单壁锐钛矿(101)纳米管的构型.我们计算并比较了这些纳米管的每单位TiO2的总能量、应变能和能隙等性质,如表2所示.DFTB方法计算的Ti―O键长与PBE方法的相差很小(0.001-0.010 nm),但是能隙结果相差较大.这是由于纯DFT方法会低估能隙的大小,而DFTB方法计算的能隙在4.0-4.6 eV之间,这与以前的实验33和计算结果30,31在定性上比较一致.例如,实验上通过测量溶液胶体相TiO2纳米管光学性质推测其能隙大约为3.87 eV.因此,我们选择DFTB方法应用到TiO2纳米管体系,其能量和能隙随半径和手性的变化趋势是一致的,不影响结果的定性分析.

DFTB计算结果表明:三种纳米管的应变能均为正值,随着管径增加,管壁的曲率减小,管体形变逐渐减小,管径越大键长变化越不明显.当管径增加至3.0 nm左右时,纳米管的几何结构开始接近纳米片,相应的应变能也呈现递减并逐渐趋近于零的趋势.在管径相同的情况下,(n,0)构型的纳米管的应变能是三种类型纳米管中最低的.这是由于60%的Ti―O键(所有的Ti―O2c键和部分Ti―O3c键)都与管轴共面,卷曲对管体带来的形变是最小的,晶胞参数c几乎在管径增加的过程中没有任何变化,并且从键长数据中可以看出,只有与管轴不共面的Ti―O3c键随管径变化较为明显.(0,m)纳米管外层的Ti―O3co和Ti―O2co键随管径减小呈现增大的趋势,内层的Ti―O3ci和Ti―O2ci键则随着管径减小而减小,管壁外部被拉伸,而管壁内部受到压缩,晶胞参数c随管径减小而增大,这是由于(0,m)纳米管中60%的Ti―O键垂直于管轴,因此卷曲对管体会造成较大的影响,所带来的应力和形变要大于(n,0)纳米管.如图2(a)所示,和(n,0)、(0,m)纳米管相比,(n,m)纳米管的Ti―O键与管轴均成一定的夹角,几乎所有的Ti―O键都在卷曲的过程中受到挤压或者拉伸,使得(n,m)纳米管的应力最大.

表1 优化后的锐钛矿晶体与(101)纳米单层片的几何构型及能量Table 1 Optimized geometry and energy of anatase bulk and single layer(101)nanosheet

表2 不同构型锐钛矿(101)纳米管的几何及能量信息Table 2 Geometry and energy information of different types of anatase(101)nanotubes

能隙计算的结果如图2(b)所示,当管直径增加的时候,能隙都是减小的,唯一例外的是(6,0)管.比较(6,0)管和其它(n,0)管可知,由于应力较大,(6,0)纳米管发生重构现象,管壁变薄,第三和第四层的Ti原子压缩成一层,第二和第五层的O原子也压缩成一层,两个临近原子层间Ti―O作用削弱而原子层间相互作用增强,引起Ti与O之间电子态的杂化造成了能隙的突变.而在管径相同的情况下,(n,0)纳米管能隙都小于(0,m)纳米管.对于(n,m)(n＝m)纳米管,当管径小于3.0 nm时,其能隙大于(n,0)和(0,m)纳米管;当管径大于3.0 nm而小于4.0 nm时,其能隙介于(n,0)和(0,m)纳米管之间,当其管径大于4.0 nm时,其能隙是三种纳米管中最小的.在本文所涉及的纳米管中,(4,4)纳米管的能隙最高,达到4.58 eV,相比晶体能隙的计算值上升了0.36 eV.

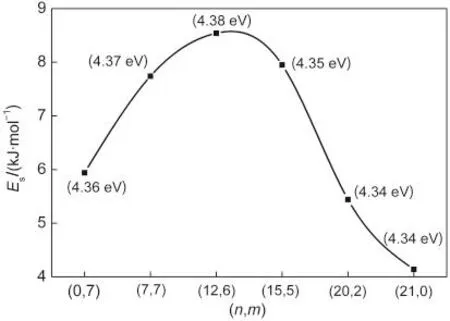
图3 相同管径不同手性纳米管的应变能和能隙随手性变化的关系Fig.3 Relationships between strain energy,band gap energy and chiralities of the same diameter anatase(101)nanotubes Band gap energy is in the bracket.

为了研究相同管径不同手性的纳米管的性质差别,我们构建了一系列管径在2.60-2.75 nm之间,手性不同的纳米管,随着n/m的增大,纳米管能隙变化很小(4.34-4.38 eV),而其应变能呈现先增大后减小的规律,如图3所示,变化趋势大致为:(n,0)＜(n,m) (n/m＞10)＜(0,m)＜(n,m)(n/m＜10).

4 结论

描述了从三维周期性晶体出发构建不同手性的锐钛矿(101)纳米管的过程,通过紧束缚密度泛函理论(DFTB)方法结合周期性模型对其进行理论研究,讨论了不同管径下手性纳米管的几何结构及电子性质,得到以下结果.(1)相同手性纳米管随着管径的增加,管稳定性亦增加,应变能逐渐减小.(2)应力对Ti―O键的作用具有选择性与方向性,与管轴共面的Ti―O键几乎没有受到应力作用的影响,而与管轴不共面的Ti―O键,管轴与其夹角越大,所受的应力越大.(3)从晶体到纳米片再卷曲成纳米管,体系的能隙逐渐增大.除了(6,0)管,其它纳米管随着管径的增加而减小.这是由于小管径的(n,0)纳米管由于应变能大而引发重构,Ti与O之间电子态的杂化而出现异常.(4)在管径相同的前提下,不同手性的纳米管能隙变化不大,随着n/m的增大,应变能呈现先增大后减小的规律,其中,(n,0)纳米管由于与锐钛矿(101)纳米管应变能随手性变化趋势大致为:(n, 0)＜(n,m)(n/m＞10)＜(0,m)＜(n,m)(n/m＜10).

(1) Fujishima,A.;Honda,K.Nature 1972,238,37.doi:10.1038/ 238037a0

(2)Adachi,M.;Murata,Y.;Okada,I.;Yoshikawa,S. J.Electrochem.Soc.2003,150,G488.

(3)Anpo,M.;Takeuchi,M.J.Catal.2003,216,505.doi:10.1016/ S0021-9517(02)00104-5

(4)Grimes,C.A.;Ong,K.G.;Varghese,O.K.;Yang,X.P.;Mor, G.;Paulose,M.;Dickey,E.C.;Ruan,C.M.;Pishko,M.V.; Kendig,J.W.;Mason,A.J.Sensors 2003,3,69.doi:10.3390/ s30300069

(5) Imai,H.;Matsuta,M.;Shimizu,K.;Hirashima,H.;Negishi,N. Solid State Ionics 2002,151,183.doi:10.1016/S0167-2738(02) 00708-7

(6) Kasuga,T.;Hiramatsu,M.;Hoson,A.;Sekino,T.;Niihara,K. Adv.Mater.1999,11,1307.doi:10.1002/(SICI)1521-4095 (199910)11:15＜1307:AID-ADMA1307＞3.0.CO;2-H

(7)Michailowski,A.;AlMawlawi,D.;Cheng,G.S.;Moskovits,M. Chem.Phys.Lett.2001,349,1.doi:10.1016/S0009-2614(01) 01159-9

(8)Mor,G.K.;Carvalho,M.A.;Varghese,O.K.;Pishko,M.V.; Grimes,C.A.J.Mater.Res.2004,19,628.doi:10.1557/ jmr.2004.19.2.628

(9) Mor,G.K.;Shankar,K.;Paulose,M.;Varghese,O.K.;Grimes, C.A.Nano Lett.2006,6,215.doi:10.1021/nl052099j

(10)Varghese,O.K.;Gong,D.W.;Paulose,M.;Ong,K.G.;Grimes, C.A.Sens.Actuators B 2003,93,338.doi:10.1016/S0925-4005

(03)00222-3

(11) Zhou,Y.K.;Cao,L.;Zhang,F.B.;He,B.L.;Li,H.L. J.Electrochem.Soc.2003,150,A1246.

(12) Hu,Y.F.;Jiang,G.;Meng,D.Q.;Kong,F.J.Acta Phys.-Chim. Sin.2010,26,1664.[胡燕飞,蒋 刚,蒙大桥,孔凡杰.物理化学学报,2010,26,1664.]doi:10.3866/PKU.WHXB20100607

(13) Xu,L.;Tang,C.Q.;Huang,Z.B.Acta Phys.-Chim.Sin.2010, 26,1401.[徐 凌,唐超群,黄宗斌.物理化学学报,2010, 26,1401.]doi:10.3866/PKU.WHXB20100526

(14) Gong,J.J.;Lai,Y.K.;Lin,C.J.Electrochim Acta 2010,55, 4776.doi:10.1016/j.electacta.2010.03.055

(15) Kasuga,T.;Hiramatsu,M.;Hoson,A.;Sekino,T.;Niihara,K. Langmuir 1998,14,3160.doi:10.1021/la9713816

(16) Lai,Y.K.;Sun,L.;Zuo,J.;Lin,C.J.Acta Phys.-Chim.Sin. 2004,20,1063.[赖跃坤,孙 岚,左 娟,林昌健.物理化学学报,2004,20,1063.]doi:10.3866/PKU.WHXB20040901

(17)Li,D.;Chen,H.C.;Li,J.H.;Zhou,B.X.;Cai,W.M.Acta Phys.-Chim.Sin.2011,27,2153. [李 迪,陈红冲,李金花,周保学,蔡伟民.物理化学学报,2011,27,2153.]doi:10.3866/ PKU.WHXB20110910

(18) Li,J.;Yun,H.;Lin,C.J.Acta Phys.-Chim.Sin.2007,23,1886. [李 静,云 虹,林昌健.物理化学学报,2007,23,1886.] doi:10.3866/PKU.WHXB20071211

(19) Hoyer,P.Langmuir 1996,12,1411.doi:10.1021/la9507803

(20)He,T.;Zhao,M.W.;Zhang,X.J.;Zhang,H.Y.;Wang,Z.H.; Xi,Z.X.;Liu,X.D.;Yan,S.S.;Xia,Y.Y.;Mei,L.M.J.Phys. Chem.C 2009,113,13610.doi:10.1021/jp9032244

(21)Meng,Q.Q.;Wang,J.G.;Xie,Q.;Li,X.N.J.Phys.Chem.C 2010,114,9251.doi:10.1021/jp100389f

(22) Ivanovskaya,V.V.;Enyashin,A.N.;Ivanovskii,A.L. Mendeleev Commun.2003,5.

(23) Enyashin,A.N.;Seifert,G.Phys.Status Solidi B 2005,242, 1361.doi:10.1002/pssb.200540026

(24)Wang,J.G.;Wang,J.;Ma,L.;Zhao,J.J.;Wang,B.L.;Wang, G.H.Physica E 2009,41,838.doi:10.1016/j.physe. 2008.12.018

(25) Liu,Z.J.;Zhang,Q.;Qin,L.C.Solid State Commun.2007, 141,168.doi:10.1016/j.ssc.2006.09.055

(26) Bandura,A.V.;Evarestov,R.A.Surf.Sci.2009,603,L117.

(27)Hossain,F.M.;Evteev,A.V.;Belova,I.V.;Nowotny,J.;Murch, G.E.Comput.Mater.Sci.2010,48,854.doi:10.1016/j. commatsci.2010.04.007

(28) Evarestov,R.A.;Zhukovskii,Y.F.;Bandura,A.V.;Piskunov,S. J.Phys.Chem.C 2010,114,21061.doi:10.1021/jp106929f

(29) Evarestov,R.A.;Zhukovskii,Y.F.;Bandura,A.V.;Piskunov, S.;Losev,M.V.J.Phys.Chem.C 2011,115,14067.doi: 10.1021/jp2027737

(30) Evarestov,R.A.;Zhukovskii,Y.F.;Bandura,A.V.;Piskunov,S. Cent.Eur.J.Phys.2011,9,492.doi:10.2478/ s11534-010-0095-8

(31) Ferrari,A.M.;Szieberth,D.;Noel,Y.J.Mater.Chem.2011,21, 4568.doi:10.1039/c0jm03257c

(32) Zheng,G.;Witek,H.A.;Bobadova-Parvanova,P.;Irle,S.; Musaev,D.G.;Prabhakar,R.;Morokuma,K.;Lundberg,M.; Elstner,M.;Köhler,C.;Frauenheim,T.J.Chem.Theory Comput.2007,3,1349.doi:10.1021/ct600312f

(33) Burdett,J.K.;Hughbanks,T.;Miller,G.J.;Richardson,J.W.; Smith,J.V.J.Am.Chem.Soc.1987,109,3639.doi:10.1021/ ja00246a021

March 13,2012;Revised:May 29,2012;Published on Web:May 29,2012.

A Tight-Binding Density Functional Theory Study on Single-Walled Nanotubes from Anatase TiO2(101)Sheets

LIU Hao LIN Meng-Hai TAN Kai*
(Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry,State Key Laboratory of Physical Chemistry of Solid Surfaces,College of Chemistry and Chemical Engineering,Xiamen University,
Xiamen 361005,Fujian Province,P.R.China)

A series of chiral anatase(101)nanotubes(NT),which we refer to as(n,0),(0,m),and(n,m), can be formed by rolling up two-dimensional periodic anatase TiO2(101)single layer sheets.Optimized parameters of the atomic and electronic structures of these nanotubes have been calculated using a tight-binding density functional theory method(DFTB).Their band gaps(Eg)and strain energies(Es)have been analyzed as functions of NT diameter.Except for(6,0),the strain energy and the band gap of all the nanotubes of various chirality decrease as the diameter increases.We also find that the strain energy increases first and then decreases rather than varying monotonically with almost constant band gap when n/m ranges from zero to infinitely large.

Tight-binding density functional theory method;TiO2;Anatase;Nanotube

10.3866/PKU.WHXB201205291

O641

∗Corresponding author.Email:ktan@xmu.edu.cn;Tel:+86-592-2182826.

The project was supported by the National Natural Science Foundation of China(20873107)and National Key Basic Research Program of China (973)(2011CB808504).

国家自然科学基金(20873107)和国家重点基础研究发展规划项目(973)(2011CB808504)资助