近景摄影测量中如何选择交向摄影

李 岩 方子岩

(1.嘉兴市秀洲区土地勘测信息中心，浙江嘉兴 314031;2.东南大学，江苏南京 210096)

近景摄影测量常常使用交向摄影，交向摄影使用单个相机分别在两个摄站对目标摄影，两个摄站上主光轴相交于目标，两个摄站的距离、交向角的大小等对摄影质量有影响。以下从正直摄影出发，讨论如何选择交向摄影。

1 正直摄影

立体摄影机使用两个参数一样的摄影机，固定在基线架上摄影，通常称为正直摄影，得到理想像对，理想像对的左、右两张像片的主光轴在一个平面内垂直于摄影基线。在近景摄影测量中，由于对摄影基线长度的要求非常小，一般可用立体摄影机进行，每次摄影可以获得一个理想像对，如图1所示。

图2为正直摄影，设物体中心点M的空间坐标为XYZ，对应的像点坐标为 x1，z1和 x2，z2，左右视差 p=x1-x2。有如下关系

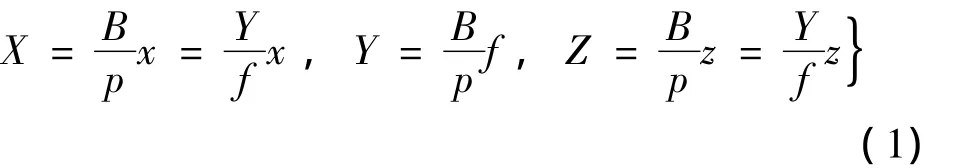
上式微分并转为中误差，同时设mx=mx1=mx2=mz，则有

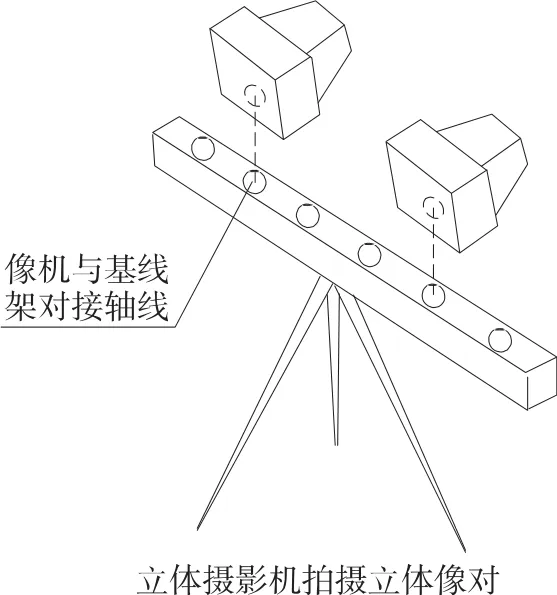
图1

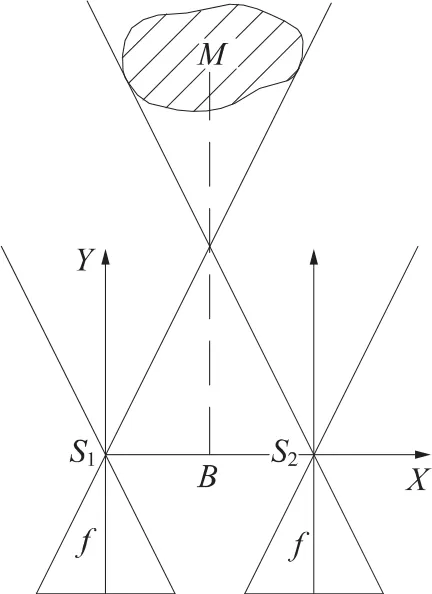
图2 正直摄影

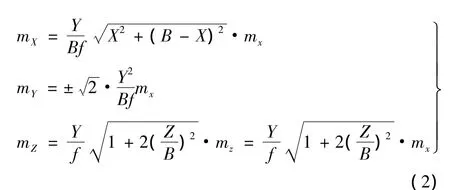
中心点M的空间坐标精度为

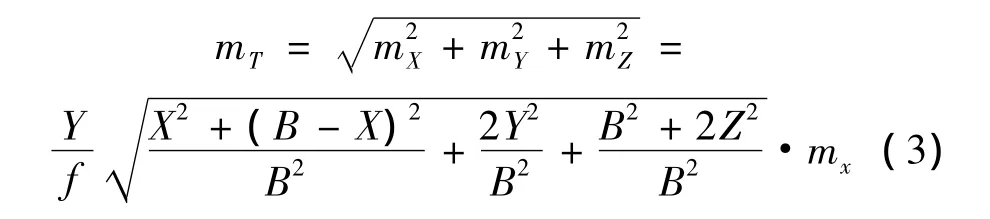
由(2)式和(3)式可得出

①设 F=X2+(B-X)2，则时，有=4＞0，所以时F有极小值，说明位于基线中垂线上的点mX最小。

②由mZ=可知，当Z=0时，位于过投影中心的坐标平面上的点其mz最小。

③由(3)式可知，减小竖距Y，增大基线B，可明显提高点位精度mT。

因此，将物体中心点M设置在XY平面内，且在基线的中垂线上，即Z=0，X时，正直摄影的图形较佳(未考虑B和Y两个因素时只能说是较佳)，其物体中心点M的精度为

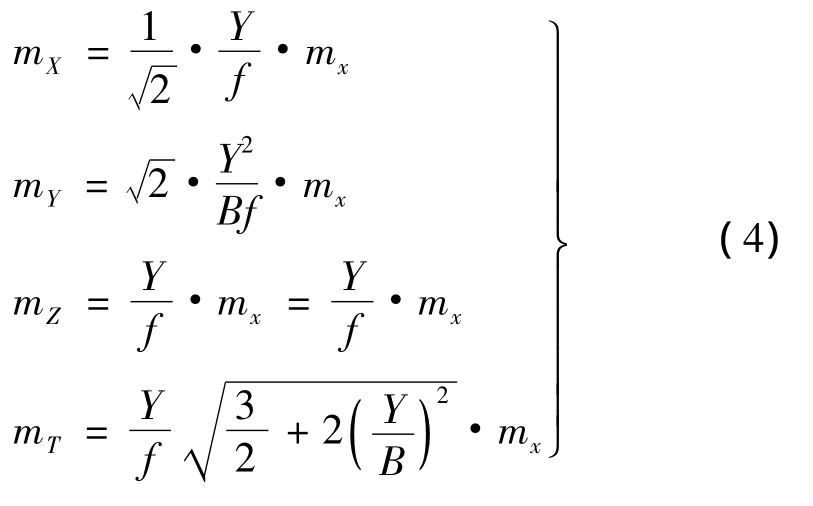
2 交向摄影图形和物体中心点M的精度

交向摄影图形可在图2的基础上，使左右像片主光轴向着基线中垂线同时转动一个摄影方向角φ。M点在左右像片同名像点的投影光线与Y轴方向的夹角用γ/2表示，称为像点张角，可用以描述点的位置，如图3所示。

现取左片来讨论，由于像片是在图2正直摄影的基础上转过φ角而得到，因而可通过方向角φ将交向摄影像片改化成“伪正直摄影像片”，然后进行精度分析。

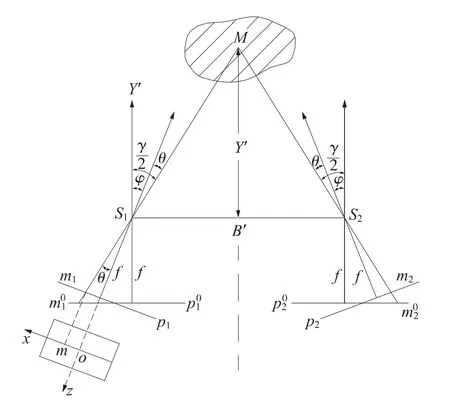
图3 交向摄影图与中心点

可参照摄影测量中有关“同摄站水平像片和倾斜像片之间的坐标关系式”而立即得到

微分(5)式

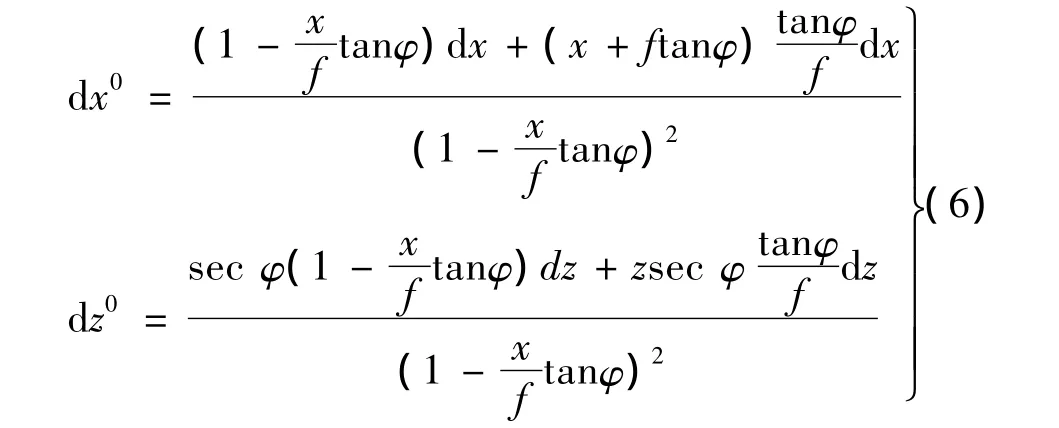
由(5)式得

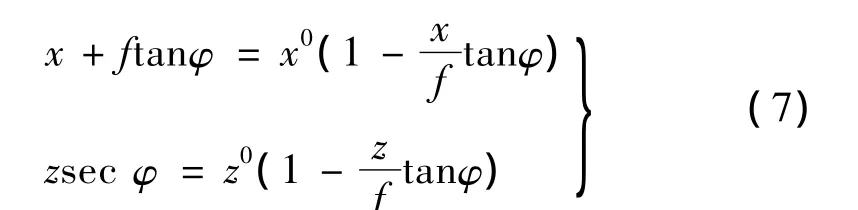
(7)式代入(6)式经整理后可得

由图3可知

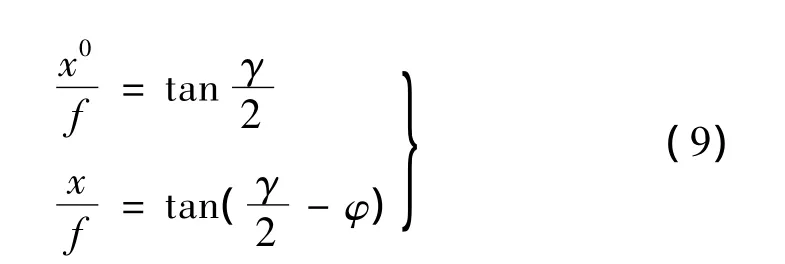
将(9)式代入(8)式并转为中误差

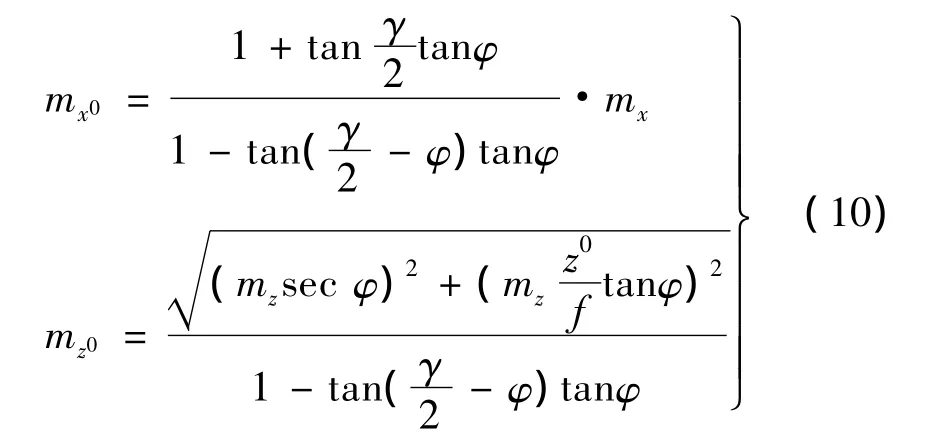
如前所述，若将物体中心点M设置在与摄影物镜同一高程水平面上，即z=z0=0，则(10)式变为

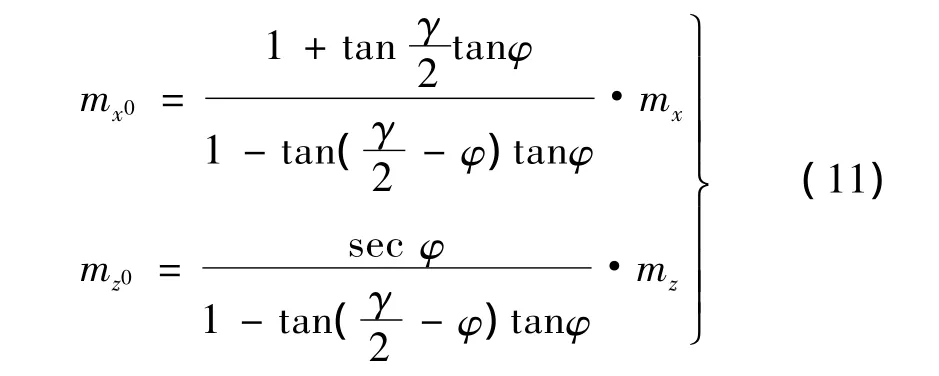
将(11)式中的mx0和mz0分别代换(4)式中的mx和mz，并将伪正直摄影的Y'和B'代入，得交向摄影的中误差公式

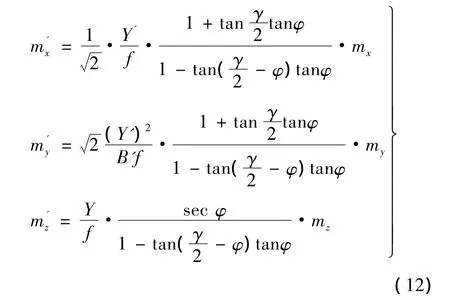
利用三角公式将(12)式改化可得

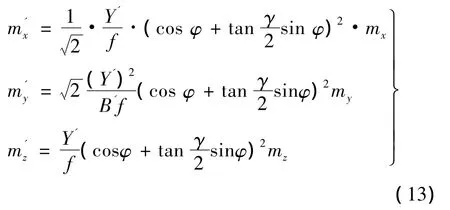
由图4，γ/2=φ+θ。设mx=mz，则交向摄影时物体中心点M的点位精度为

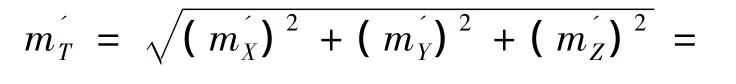
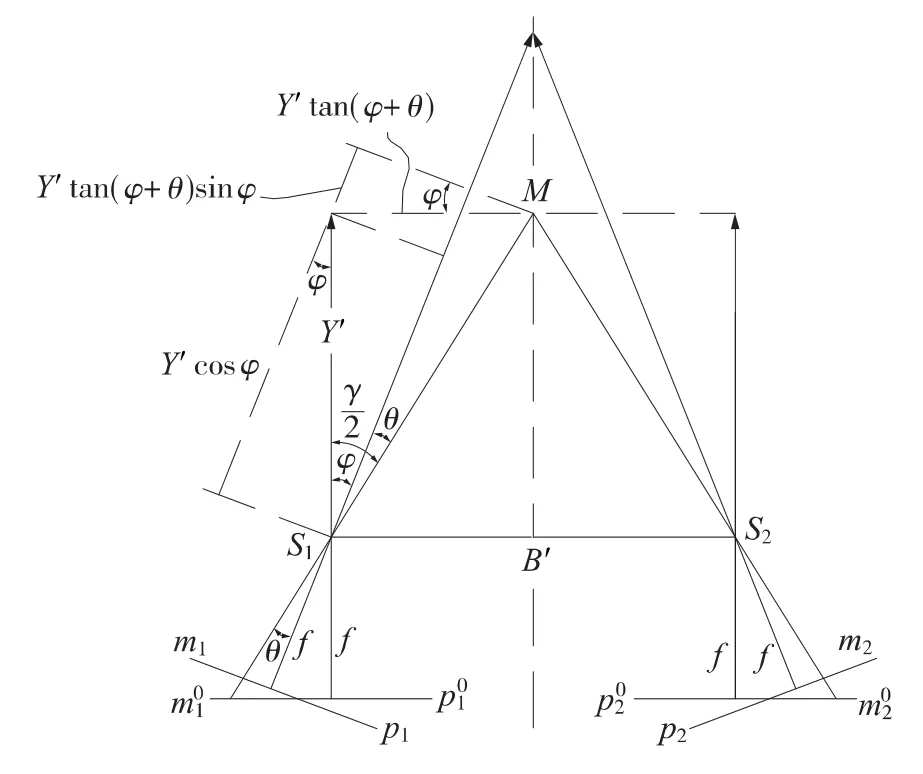
图4 交向摄影中心点精度分析

3 交向摄影图形及精度分析

假定γ/2=φ，即左右光轴交于物点M，且S至M的距离 l为定值(如图5)，此时:Y'=l cosφ，B'/2=l sinφ，B'/Y'=2tanφ，代入(12)得出

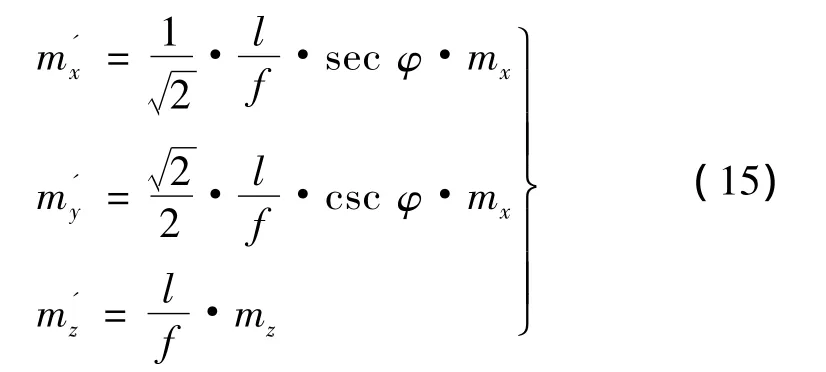
点位精度为

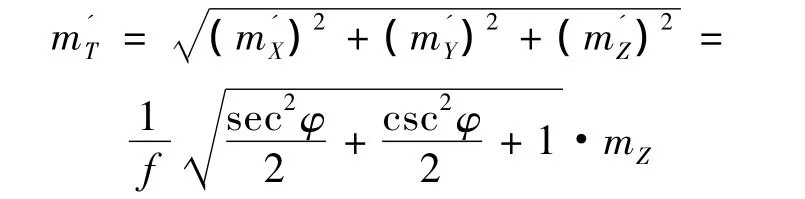
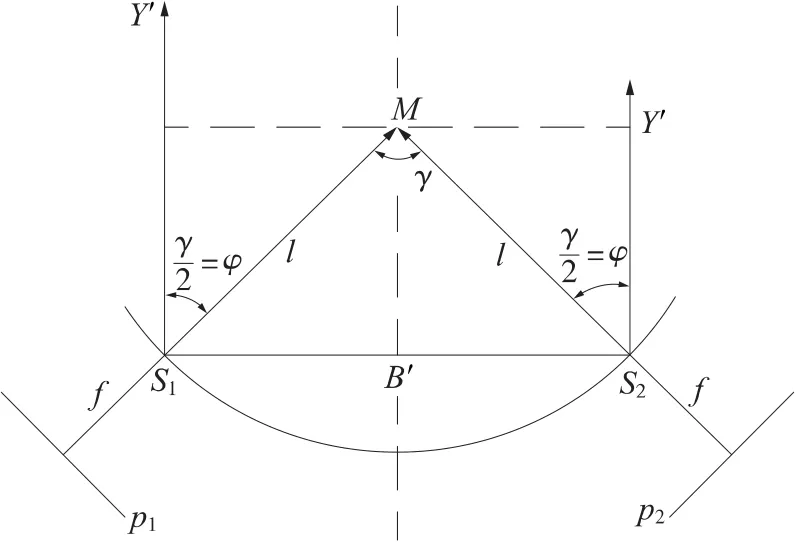
图5 交向摄影图形及精度分析

假定像点投影光线与光轴的张角θ为定值。

θ为定值即M点的像片坐标不变，此时改变φ时，交角 γ/2=φ+θ随之变化，在(14)式中，设 F2=)，且有，令=0，即 cosθ=0或 cos(2φ +2θ)=0，但 θ不可能为90°，故有2φ +2θ=90°，φ +θ=45°，

4 结论

物体中心点M的两条同名投影光线相交成直角，即 φ +θ=45°时，点位精度最佳，且当 θ=0，φ =45°时最优。所以交向摄影时，左右光轴对准物体中心点摄影以φ=45°的图形结构最佳。

［1］冯文灏.近景摄影测量［M］.武汉.武汉大学出版社，2002

［2］方子岩.摄影测量学［Z］.南京:东南大学，2009

［3］方子岩.交向摄影的最佳图形［J］.四川测绘，1992，15(2)

［4］学科组.误差理论与测量平差基础［M］.武汉:武汉大学，2003