基于粒子群算法的铁路客票预售期研究

王红爱，吕晓艳，朱建生，周亮瑾

(中国铁道科学研究院 电子计算技术研究所，北京 100081)

铁路客票发售和预订系统 (以下简称客票系统) 自1996年开始应用以来，实现了全路联网售票，推出窗口售票、自动售票机售票、电话订票、互联网购票等多种方式，极大地方便了旅客购票。为避免铁路客流高峰时期的购票拥挤，一般需要调整客票预售期。目前，主要依据历史数据和专家经验制定客票预售期，人为因素较多。因此，提出基于粒子群算法的铁路客票预售期计算模型，以预测售票量为基础，通过调整客票发售期的适用度函数，达到每日均衡发售客票的目标。

1 粒子群算法概述

粒子群优化算法 (PSO) 是一种进化计算技术，1995年由 Eberhart 和 kennedy 提出[1]，源于对鸟群捕食行为的研究。PSO 是一种基于迭代的优化算法，系统初始化为一组随机解，通过迭代搜寻最优值。在每一次迭代中，粒子通过跟踪2个极值来更新自己，一个极值是粒子本身所找到的最优解，称为个体极值 pbest；另一个极值是整个种群当前找到的最优解，称为全局极值 gbest。如果将部分粒子代替整个种群进行搜索，得到的极值是局部极值。粒子在搜索过程中，根据个体极值和全局极值，更新自己的速度和位置。

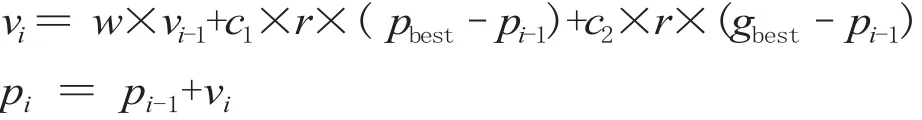
式中：vi为粒子速度；w 为惯性权重，用于平衡全局搜索和局部搜索，可以改善粒子群优化算法，使群体勘探和开发能力在整个计算过程中合理分配；pi是当前粒子位置；r是介于 (0，1) 之间的随机数；c1、c2是学习因子，通常 c1＝c2＝2；每一维粒子的速度都会被限制在一个最大速度 vmax之内，如果某一维更新后的速度超过用户设定的 vmax，那么这一维的速度就被限定为 vmax。

每个粒子在解空间内不断搜索与更新其个体极值和全局极值，直到满足条件后停止。基本粒子群算法如图1所示。

具体实现过程如下。

第1步：初始化粒子群：初始化粒子群中所有粒子的特征，包括粒子个数、速度和位置。

第2步：使用根据优化问题目标定义的适应度函数对所有粒子进行评价。

第3步：将种群中每个粒子的适应度值与其个体极值比较，如果适应度值大于个体极值，则更新该粒子的个体极值。

第4步：将种群中每个粒子的适应度值与全局极值比较，如果适应度值大于全局极值，则更新每个粒子所在种群的全局极值。

第5步：不断迭代粒子速度及位置。

第6步：重复以上步骤，直到满足算法的迭代停止条件 (达到一定误差或者达到最大循环次数)为止。

2 建立模型

2.1 客票预售期模型

基于 PSO 算法建立铁路客票预售期调整优化模型，如图2所示。该模型的思想是：预测预售期售票量，基于粒子群算法计算售票量的平滑度，对预售期进行优化，使得售票量的平滑度达到最优。

2.2 平滑度目标函数

为均衡系统资源，平滑预售期内日售票量差异，设置目标函数。

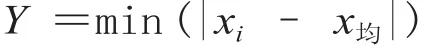
式中：xi为每日售票量；x均为预售期内平均每日售票量。

2.3 参数设置

根据铁路客票预售期的实际情况，设置模型参数。

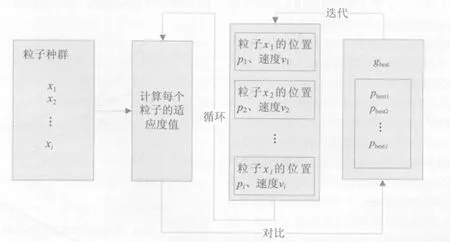
图1 基本粒子群算法

图2 基本粒子群算法的应用模型图

（1）粒子数。一般取 20～40。一般情况下，取 10个粒子即可以得到较好的效果。对于比较难的问题或者特定问题，粒子数可以取到 100～200。铁路普通票的最大预售期为 20 天，取 20个粒子。

（2）vmax。最大速度决定粒子在循环中的最大移动距离，通常设定为粒子的范围宽度。例如，粒子 (x1，x2，…，xi) 属于[-5，5]，则 vmax的大小为10。

（3）学习因子。c1和 c2通常等于 2。不过在文献中也有其他的取值，但是一般 c1等于 c2，并且范围在 0和4之间。在此，取c1＝c2＝2.5。

（4）停止条件。设置日售票量峰值与日售票量均值的差值占均值的百分比作为停止条件。

（5）惯性权重。惯性权重表示原来的速度在下一步迭代中所占的比重，通常取较大值时，算法具有较强的全局搜索能力；反之，算法具有较强的局部搜索能力。对于 Schaffer 的f6函数，当 vmax≤2时，使用接近于1的惯性权重；当vmax≥3 时，取w＝0.8 较好[2]。如果没有 vmax的信息，使用 0.8 作为权重也是一种很好的选择。一般设置 w 随着计算的进行而不断减小，以使得算法在运行初期有较好的全局搜索能力，而在末期有比较好的局部搜索能力。根据经验，w 的取值范围为 [0，1.4]比较合适，但是通常当 w 取值在 [0.8，1.2]之间时，算法收敛较快。基于此，取惯性权重值为 0.8 。

3 模型仿真

以2012年春运节前客票销售数据为样本数据集，进行平滑度仿真实验，确定预售期调整优化方案。初始数据集：{1 763 447，1 530 622，1 087 933，1 038 916，1 000 560，1 477 520}。粒子范围为[1 000 560，1 763 447]，vmax的取值为 762 887。预售期内售票量的平滑度仿真结果如图3所示，实验统计量如表1所示。从图3可见，不同的预售期售票曲线的平滑度不同。从表1可见，设置预售期为 13d时，评价指标综合最佳，平滑度最优。从减轻系统压力方面考虑，建议调整预售期为 13 d。

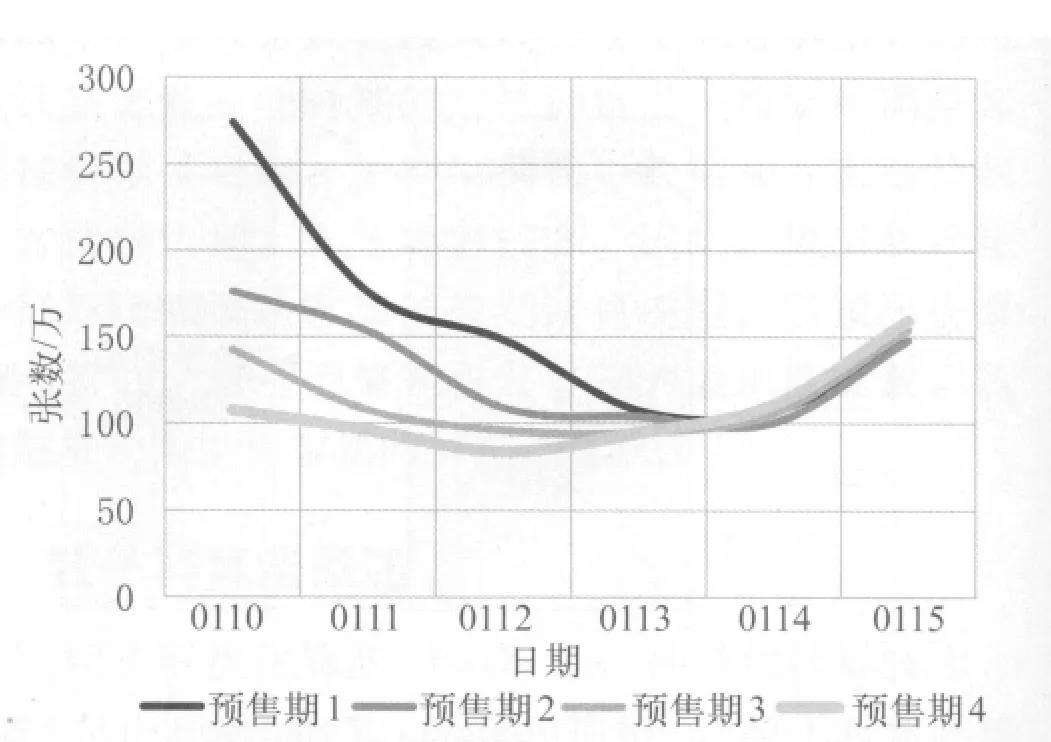
图3 预售期内售票量的平滑度仿真图

仿真实验的结果表明，通过 PSO 算法调整预售期可以平滑日售票量，减轻系统压力。但是在图3中的最优曲线表明，在优化过程中，存在指定售票日预售期内售票量高峰转移的现象，因此该解为局部最优解，这与权重参数 w 的选取有关。

表1 仿真实验统计量

4 结束语

基于粒子群算法建立铁路客运预售期模型，研究结果表明，该模型能够较好地优化预售期内日售票量的平滑度，对于均衡系统资源、制定合理的预售期具有一定指导意义。2011年开始全面实现互联网售票及电话订票业务，铁路客运售票量在特定时期如春运、暑运、十一、五一等阶段不同售票方式的历史数据有限，因此，该仿真实验存在局限性。在下一步的研究中，一方面可在历史数据充足的条件下对适用度函数的参数进行优化，另一方面可以根据不同的售票方式建立多层次应用模型，完善算法。

[1]Kennedy J，Eberhart R C. Particle Swarm Optimization[M]//IEEE Service Center. Proceedings of IEEE International Conference on Neural Networks. Piscataway，New Jersey：IEEE Service Center，1995，4：1942-1948.

[2]Yuhui Shi，Russell Eberhart. A Modified Particle Swarm Optimizer[M]//IEEE Press. Proceedings of IEEE World Congress on Computational Intelligence in：Evolutionary Computation. Anchorage，AK USA：IEEE Press，1998：69-73.