基于形态距离的真空热试验数据相似性度量研究

谢吉慧，郄殿福

（1. 可靠性与环境工程技术重点实验室； 2. 北京卫星环境工程研究所：北京 100094）

0 引言

真空热试验是航天器总装、测试、试验（AIT）阶段必不可少的测试项目。真空热试验过程中可能出现硬件设备工作异常、某些类型工作参数设置错误等问题，这些问题须通过对数据异常的监测来发现。目前对试验数据异常的监测与分析主要依靠人工完成。由于数据量庞大，人工监测的负担较重，实时性和全面性也难以保证，所以急需自动化的监测手段以降低人工成本，提高监测效率，同时增强试验过程的安全性。本文从试验数据的相似性特征出发，采用数据挖掘的方法识别出离群变化行为，以提高对试验过程异常情况监测的自动化程度和及时性。

1 基于形态距离的真空热试验数据相似性度量方法

1.1 基本原理

真空热试验中试验产品的不同部件上会布置大量测温点，由于粘贴位置的关系，邻近部位测温点具有相近的幅值和相似的变化趋势；另外，在部组件热真空试验中，试验要求各控温点按照统一步调与幅值进行高低温循环，因此，测点数据间的相似性在各种航天器真空热试验中普遍存在。可以利用这一特性进行试验过程的异常监测，具体的实现原理为：对试验过程中各测量点的数据进行相似性聚类，对同类测点新产生的数据进行离群检测，判断哪些测点出现了脱离“组织”行动的异常行为，提示试验人员关注（如图1）。

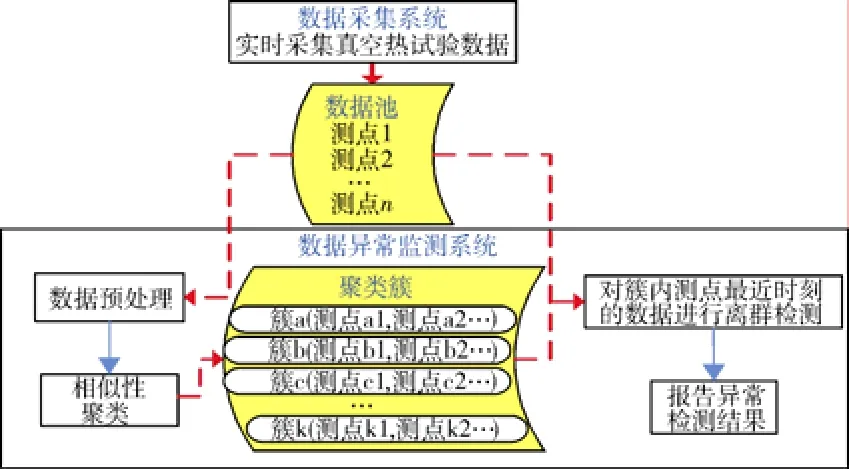
图1 真空热试验数据异常自动监测原理Fig. 1 Automatic monitoring of the abnormity of vacuum thermal test data

真空热试验数据是一种典型的时间序列。时间序列由于其自身噪声与波动性的特点，相似的时间序列会呈现多种变形，如振幅平移和伸缩、线性漂移、不连续及时间轴伸缩等[1-2]。

形态距离算法[3]基于人类视觉直观判断的经验，将时间序列变换为曲线形态特征的集合，一个时间序列的形态可以表示为（模式，时刻）对的形式。两个时间序列间的形态距离越小，它们的形态越接近。形态距离对时间序列的振幅平移、伸缩不敏感，并能支持线性漂移。

动态时间弯曲距离（dynamic time warping，简称 DTW）[4]是把时间规整和距离测度计算结合起来的一种非线性规整技术，它运用动态规划思想寻找一条具有最小弯曲代价的最佳路径，支持时间序列时间轴伸缩的相似性度量。

本文将以上两种距离度量方法有机融合，提出了一种改进DTW-形态距离算法，该算法能较好地解决时间序列的各类相似性变形问题。

1.2 度量算法及其实现

进行真空热试验数据相似性度量的实现流程如图 2所示。首先对真空热试验数据进行小波变换，提取变换后的低频尺度数据作为分析对象，实现数据的压缩和去噪；然后对低频尺度数据分别进行形态特征提取和规范化处理后，代入距离计算公式，计算得出各数据间的距离，形成相异度矩阵；最后对相异度矩阵进行聚类分析，识别出具有相似性特征的聚类簇。

对于真空热试验测量数据的相似性度量，需要确定统一的度量标准，以实现数据的自动相似性聚类。因此有必要在度量之前进行数据规范化处理，防止具有较大初始值域属性与具有较小初始值域属性相比权重过大[5]，造成度量标准不统一。

一般而言，形态特征提取在数据规范化后进行。然而，对于值域范围很小、略带小噪声的稳态数据，数据规范化会给形态特征提取带来负面影响：小噪声被放大，形态符号计算失真，如图3所示。规避这一问题的方法是将形态符号的计算安排在规范化之前进行，通过选择合理的模式区分阈值[3]过滤掉采集噪声的影响，见图2算法流程。

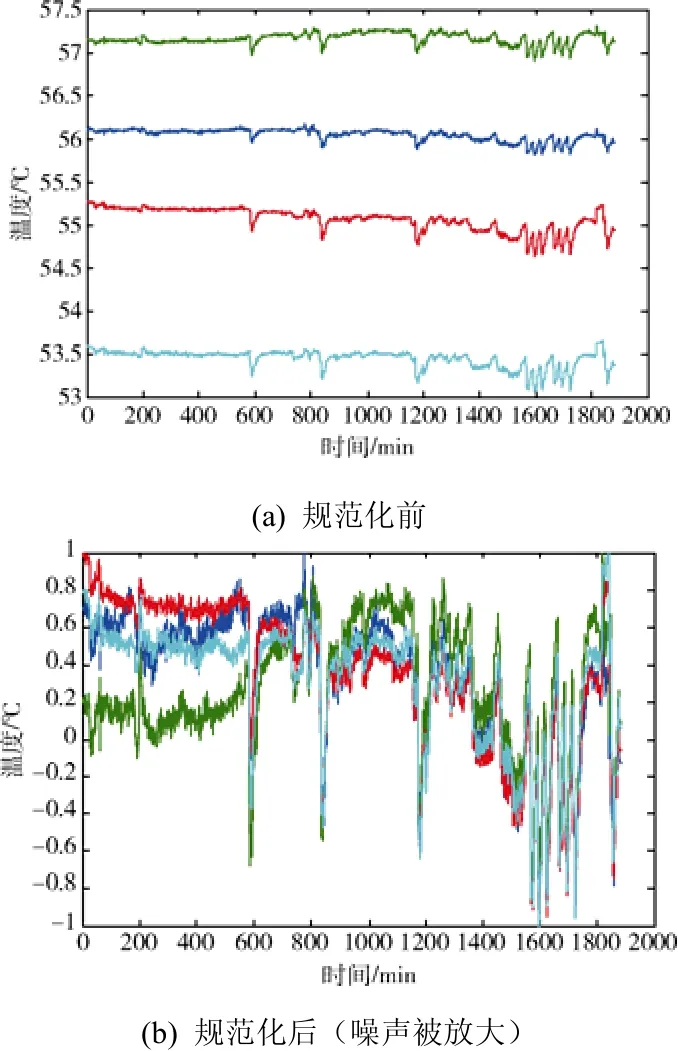
图3 规范化前后的数据曲线Fig .3 Curves before and after the standardization

Db4小波基有近似的对称性，数据分解和重构时的相位失真较小；另外，该小波基支撑长度为2N，计算复杂度和数据分解的光滑程度适中，因此，本文选用Db4作为小波基。

使用小波变换后，低频尺度数据的值域较原始数据发生了变化，因此，模式区分阈值选取时应在数据采集系统不稳定度的基础上，乘以不同尺度小波变换引发的幅值变化系数，即可消除不同层数小波变换对阈值变化的影响，实现模式区分阈值取值的通用化。

相似性度量算法具体实现步骤如下：

1）设真空热试验原始数据由n组序列组成，记为序列组{A1, A2, …, An}，对每组序列进行小波变换后的低频尺度序列组记为{B1, B2, …, Bn}。

2）设第i组低频尺度序列Bi的总长度为m，记为{Bi1, Bi2, …, Bim}，按照文献[2]中的方法，获得序列组{B1, B2, …, Bn}所对应的形态符号序列组{C1, C2, …, Cn}，其中 Ci记为{Ci1, Ci2, …, Ci(m-1)}。

3）对序列组{B1, B2, …, Bn}按照

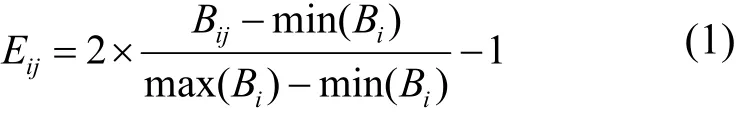
进行规范化处理，处理后的数据记为{E1, E2, …, En}。

4）对序列组两两之间进行相似性度量，获得相异度矩阵 D，距离度量计算公式如式(2)、式(3)所示。为了提升 DTW的计算效率，限定规划路径约束斜率[4]在 1/2～2范围内，搜索宽度[4]在(m−1)的 10%范围内取整数值；在进行式(2)计算时，设定提前终止计算阈值（记为ε），当Dij还未计算结束而其最小值已经大于 ε时，提前退出计算，令Dij=∞，则

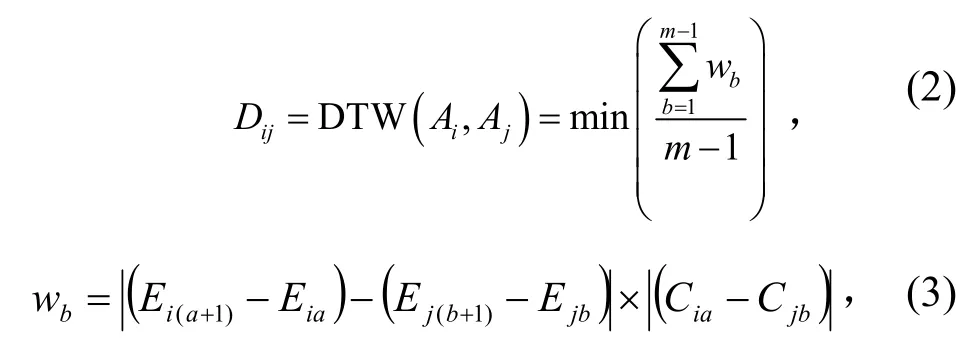
式(2)、式(3)中：a为序列 Ci的元素下标，b为序列 Cj的元素下标，1≤a≤m-1，1≤b≤m-1，|a−b|≤β。

2 试验及结果分析

2.1 试验方法

平均准确率[3]可以用来衡量聚类算法准确度，通过考察任意两组时间序列之间类属关系与人工聚类是否一致来评价聚类算法的效果。平均准确率越接近于1，聚类算法准确度越高。

本次试验采用实测数据作为数据源，使用改进DTW-形态距离算法和层次聚类法对数据源进行相似性聚类试验，通过调整相似性度量阈值α和搜索宽度β的取值，计算不同数据源和小波变换层数γ下聚类的平均准确率 ρ，统计分析参数 α、β的最佳取值范围，使得ρ取最优值。试验中相似性度量算法提前终止计算阈值ε等于α。

考虑到小波变换对样本数据的去噪效果以及变换后数据的长度（不宜太短，需要保留一定的信息量），小波变换层数γ在[5, 8]的范围内取整数值。

2.2 测试数据源选取

从目前4种典型真空热试验类型中选取4组测试数据源，这些数据源覆盖了真空热试验测量数据的各种情况，如表1所示；图4为测试数据的曲线图。

表1 测试数据源Table 1 Test data sources

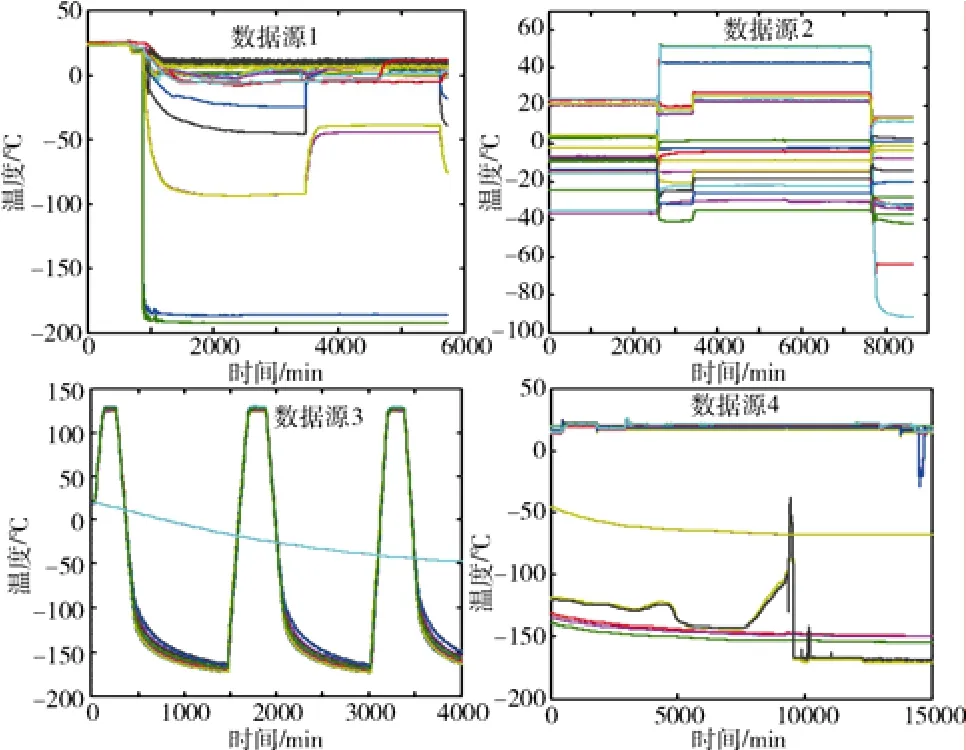
图4 测试数据源曲线Fig. 4 Test curve for the data source

2.3 相似性度量阈值测试范围

相似性度量阈值α越小，度量标准越严酷，但过小会导致相似性关系的漏报。使用改进DTW-形态距离算法和层次化聚类方法对表1中的1号和4号数据源进行聚类测试，发现α在0.02附近取值的通用性较好，如图5所示。因此，在相似性聚类试验中，α取值以0.002为间隔，最小取0.002，最大取0.04，共20组。

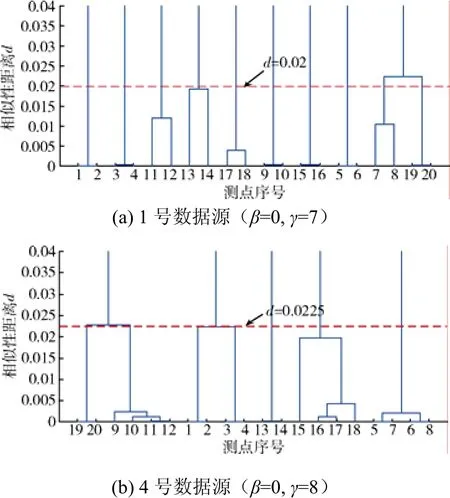
图5 1号和4号数据源聚类树Fig. 5 Cluster tree of data sources I and IV

2.4 搜索宽度测试范围

搜索宽度β越大，时间序列的允许扭曲范围越大，适应性更好，但会引入一些不合理的时间扭曲，降低聚类的准确率，同时增加计算的复杂度。因此，将搜索宽度 β限定在变换后形态符号序列长度(m−1)的 10%以内，使用改进 DTW-形态距离算法和层次化聚类方法对表1中的4组数据源进行聚类测试，发现β在｛0, 1, 2, 3｝范围内取值的聚类结果较好，因此，在相似性聚类试验中，β取值以1为间隔，最小取0，最大取3，共4组。

2.5 相似性度量阈值与搜索宽度最优取值

在以上定义的α、β、γ取值范围下，对4组测试样本进行相似性聚类试验。设定 ρ(α, β, γ, n)为不同参数对应的聚类平均准确率，其中n为测试数据源，n={1, 2, 3, 4}。定义如下2组统计数据：

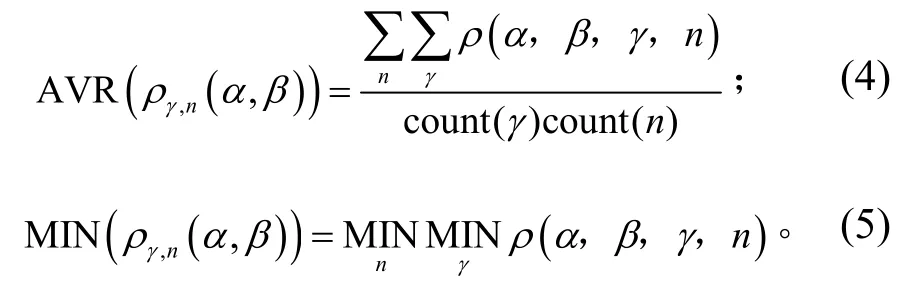
式(4)和式(5)分别统计了 ρ(α, β, γ, n)在不同 γ、不同 n取值情况下的平均值和最小值分布情况，计算结果如图 6 所示。从图 6 中可以看出：AVR(ργ,n(α, β))和MIN(ργ,n(α, β))整体趋势随着 α 值的增加在减小，当β为0、1，度量阈值α在0.028～0.032范围内时，聚类的平均准确率高。表2给出了α=0.03、β=0、γ=8时4组数据源自动聚类与人工聚类结果的对比情况。

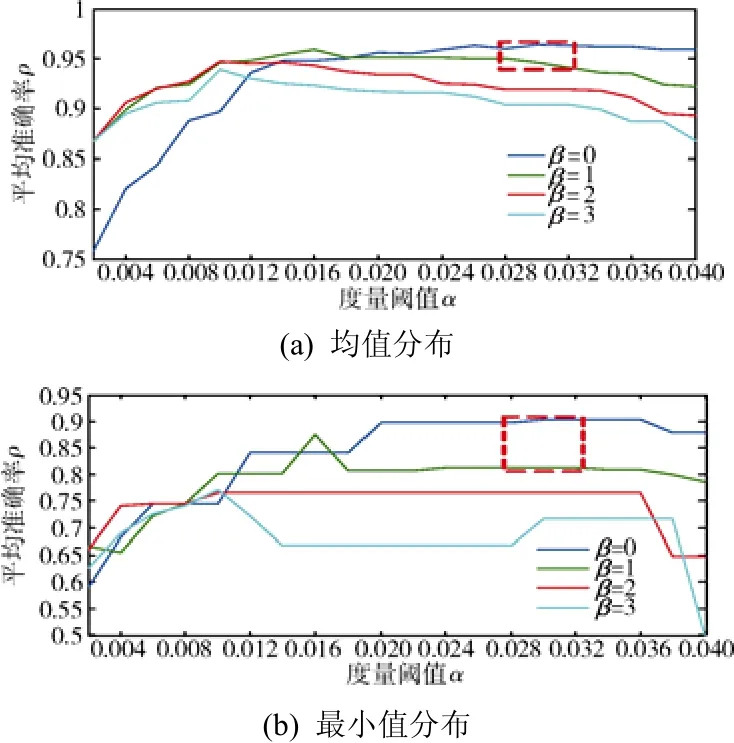
图6 平均准确率的均值分布与最小值分布Fig. 6 The average and minimum distributions of average precision

表2 聚类结果对比Table 2 Comparison between the clustering results

2.6 参数验证

使用以上参数，对随机选择的某整星试验的40路测点进行聚类，测点数据长度为4 860，对数据进行聚类验证，计算得出的平均准确率如表3所示。其中平均准确率最大值为 0.985，最小值为0.835，参数的适应性良好。

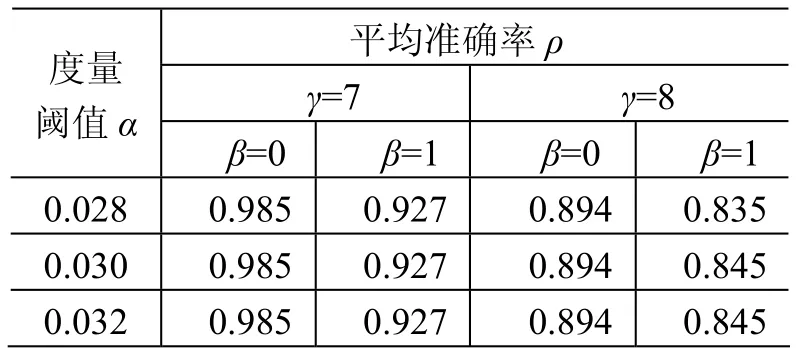
表3 某整星试验数据聚类平均准确率验证数据Table 3 Validation data of average precision for a satellite test data cluster

2.7 应用效果

为验证算法对异常数据的监测效果，选取了具有相似性特征的真实试验数据（共4个测点），对其中的1号测点数据进行调整，模拟了2种典型的异常情况：①数据异常跳动（如图7(a)中，260 min之后，1号测点出现了幅值约0.6 ℃，持续时间约15 min的尖峰跳动）；②变化趋势出现偏离。如图8(a)中，660 min之后，2、3、4号测点温度开始平缓上升，而1号测点依然维持下降趋势）。

使用本文的相似性度量算法对以上2组数据进行离群检测，相关参数取值为：α=0.03，β=0，γ=6。该算法能准确地将1号测点与2、3、4号测点划分为不同类，如图 7(b)、图 8(b)所示。算法度量出的2、3、4号测点间的相似性距离d在0.01以下，而1号测点与2、3、4号测点的相似性距离d在0.1以上，可见该算法对以上2种异常情况识别的灵敏度较高。

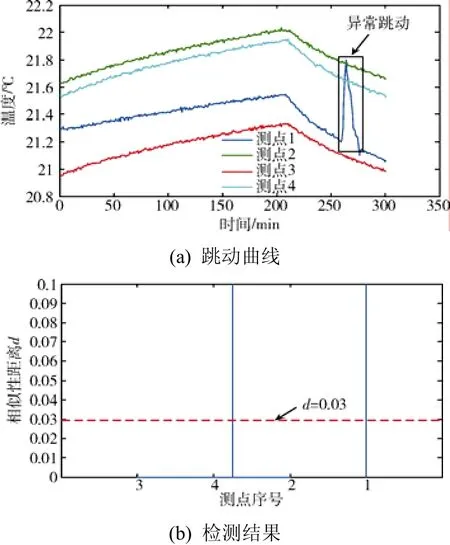
图7 数据异常跳动曲线及检测结果Fig. 7 Data abnormal jump curves and the check result

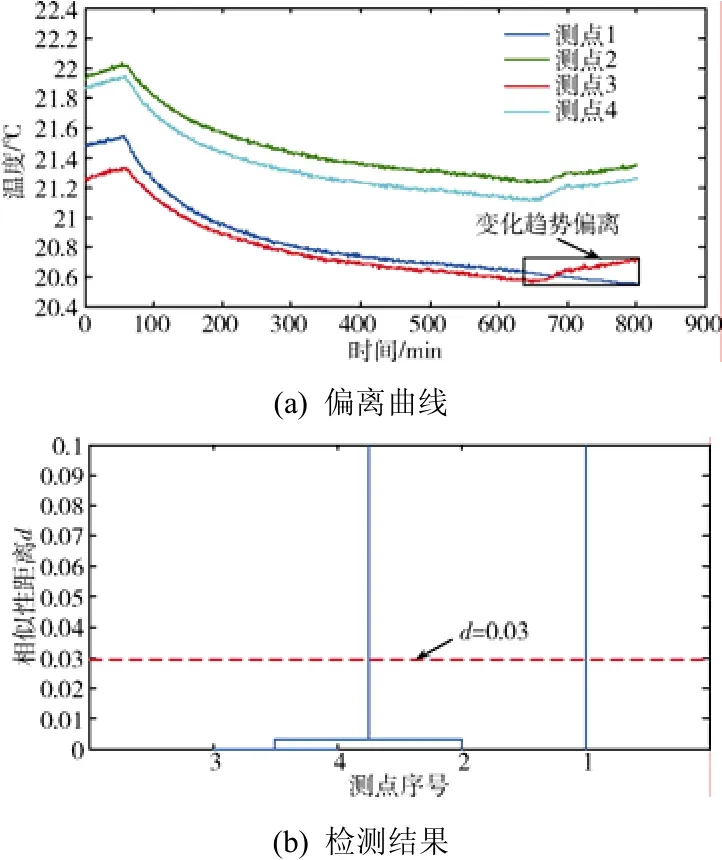
图8 数据变化趋势偏离曲线及检测结果Fig. 8 Data abnormal deviation curves and the check result

3 结束语

本文所提出的改进 DTW-形态距离算法支持振幅及时间的平移和伸缩，实现了度量参数的通用化；该算法与人工视觉分析原理接近，比较适合于进行真空热试验数据的相似性关系度量。试验数据及故障仿真分析结果证明，该算法对真空热试验数据的相似性聚类精度较高，具有较好的应用前景。进一步的研究方向包括相似性度量方法的优化和离群检测算法、参数的研究。

（References）

[1]贾澎涛, 何华灿, 刘丽, 等. 时间序列数据挖掘综述[J].计算机应用研究, 2007, 24(11): 15-18 Jia Pengtao, He Huacan, Liu Li, et al. Overview of time series data mining[J]. Application Research of Computers,2007, 24(11): 15-18

[2]Chung Fu-Lai, Fu Tak-Chung. An revolutionary approach to pattern-based time series segmentation[J]. IEEE Trans on Evolutionary Computation, 2004, 8(5): 471-89.

[3]董晓莉, 顾成奎, 王正欧. 基于形态的时间序列相似性度量研究[J]. 电子与信息学报, 2007, 29(5):1228-1231 Dong Xiaoli, Gu Chengkui, Wang Zheng’ou. Research on shape-based time series similarity measure[J]. Journal of Electronics & Information Technology, 2007, 29(5):1228-1231

[4]陈立万. 基于语音识别系统中DTW 算法改进技术研究[J]. 微计算机信息, 2006, 22(2): 267-269 Chen Liwan. Discussion of DTW programming improved way on speech recognition[J]. Control & Automation,2006, 22(2): 267-269

[5]韩家炜, 堪博. 数据挖掘概念与技术[M]. 北京: 机械工业出版社, 2007: 46