红外运动模糊图像复原技术

杨晓冬，刘 俊，张倩倩

(杭州电子科技大学信息与控制研究所，浙江杭州310018)

0 引言

经过多年的发展，图像复原这一领域出现很多有效的算法和方法，如功率谱均衡滤波、约束最小二乘、最大熵等等，而现实条件复杂多变，并不是所有的复原方法都适用在任何条件下。因此，在实际运用中，要根据实际情况，选择合适的复原方法。仔细分析运动模糊模糊的过程，建立起运动模糊的点扩散函数。运动模糊退化模型主要由两个参数组成，即模糊角度和模糊尺度。因此，现今很多运动模糊复原的问题都归结于对两种运动模糊参数的估计。本文采用方向微分算法估算出点扩散函数的模糊方向，以及利用二阶微分自相关法求得模糊尺度，从而构建点扩散函数的模糊参数，通过维纳滤波方法，消除了红外图像运动模糊。

1 运动模糊图像复原基本原理

在获取图像的瞬间，所拍摄的目标与相机发生相对运动，称为运动模糊。在所有的运动模糊中，由匀速直线运动造成图像模糊的复原问题更具有一般性和普遍意义。非匀速直线运动可近视为匀速直线运动，或者可以分解为多个匀速直线运动。获取准确的二维任意方向的匀速直线运动点扩散函数［1］的参数，是图像复原的关键。在线性移不变系统中，可以将原图像f(x，y)看成是通过一个点扩散函数h(x，y)并与加性噪声 n(x，y)相加退化成图像 g(x，y)的，图像退化过程的数学表达式［2］写为:

运动模糊图像退化复原结构示意图如图1所示:

图1 运动模糊图像退化复原原理结构图

2 模糊参数的估算

2.1 基于方向微分的模糊方向的估计

通常将原图像看作是各向同性的一阶马尔科夫过程，即原图像的自相关及其功率谱是各向同性的。图像方向微分［3］为沿规定方向上的相邻象素灰度值之差。则α方向微分:

f[α](i'，j')的计算就可以采用双线性插值的算法。双线性插值的示意图如图2所示。

双线性插值分两步进行，首先在行方向上线性插值，然后在列方向上线性插值。

当 0≤α≤90°时，由 f(i，j)和 f(i，j+1)线性插值得:

由 f(i－1，j)和 f(i－1，j+1)线性插值得:

由f1和f2线性插值得:

图像α角度的方向微分定义为图像中各个象素α角度的方向微分Δf(i，j)[α]绝对值之和，并找出最小值min(Δfα)，该值对应的角度α就是运动模糊方向。

图2 双线性插值图

2.2 基于自相关函数的模糊尺度的估计

由以上方法可以求取模糊方向，通过旋转图像，将运动模糊方向旋转到水平方向。将旋转后的模糊图像在水平方向上进行二阶微分，然后求各行的水平方向自相关，并将微分自相关图像灰度值各列求和，得到一条曲线，曲线上会出现一对共轭的相关峰，这对相关峰为尖蜂向下，对称分布在最大值尖峰两侧，两相关峰间的距离等于运动模糊点扩散函数尺度［4］的两倍。利用微分自相关法对模糊尺度估计的说明如图3所示:

图3(a)是清晰图像在水平方向上模糊10象素的模糊图像，图3(b)是模糊图像在水平方向上的二阶微分自相关曲线，从图3(b)曲线可以读出尖蜂 A(247，2)、尖蜂 B(265，2)，可以得到AB的距离AB为18象素，因此可以估计出运动模糊尺度为9象素，与实际模糊尺度误差为1象素，此误差是不可避免的，并且在接受范围内。

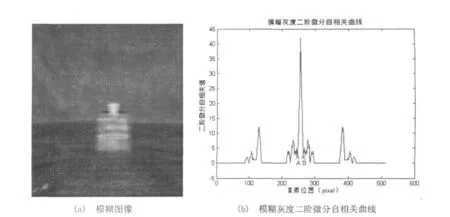
图3 模糊尺度的仿真结果

3 维纳滤波

维纳滤波［5］在抗噪性能方面效果较好，在一定程度上可以将噪声滤除，其滤波公式如示:

式中，k是个常数。当k值增大时，对噪声的抑制更明显，但是图像亮度也会变暗;而k减小时，噪声的影响就变大了。实际情况各不相同，噪声的功率谱的大小也不一样，所以要在具体应用时选择合适的常数k，以便达到最好的效果。

4 实验结果

利用上述算法对运动模糊红外图像进行处理，求得模糊尺度为9象素，误差为1象素，仿真结果如图4所示。如图4(a)为原始清晰图像，图4(b)为图4(a)运动模糊红外图像(模糊方向为100，模糊尺度为10象素，存在噪声)，图4(c)是逆滤波复原后的图像，图4(d)是维纳滤波恢复后的图像。通过比较(c)、(d)两图的复原结果可知，(c)图中存在过多的噪声，影响图像复原的结果，而图(d)更接近原始清晰图像。因此对带有噪声的红外图像，维纳滤波具有更好的恢复效果。

图4 图像退化及其复原图像

5 结束语

为解决因红外成像系统与目标之间相对运动产生的图像模糊问题，本文提出了一种图像恢复技术，将二维不规则的运动看成近似的二维匀速直线运动，从而通过微分法计算点扩散函数的参数，然后利用维纳滤波恢复图像，滤除噪声，提高图像的恢复质量。实验结果表明，通过图像恢复技术，可以实现图像的复原，而且在一定的模糊程度范围内，点扩散函数的参数估算误差较小，有效的改善图像质量。维纳滤波对于滤除噪声有明显的效果。但是此算法也有一定的局限性，并非适用于所有的非线性，不规则运动。更具一般性的算法，有待提出。

［1］ 章毓晋.图像工程(第二版)［M］.北京:清华大学出版社，2006，288－328.

［2］ 陈前荣，陆启生，成礼智.运动模糊图像的运动模糊方向鉴别［N］.国防科技大学学报，2004，26(1):41－45.

［3］ 张媛，张铃，张燕平.一种运动模糊图像的复原法［J］.微机发展，2005，15(6):28－29.

［4］ 明文华，孔晓东，屈磊.运动模糊图像的恢复方法研究［J］.计算机工程，2004，30(7):133－135.

［5］ Stem Adrian，Kruchakov Inna，Yoavi Eitan，et al.Recognition of motion blurred images by use of the method of moments［J］.Applied Optics，2002，41(11):2 164 －2 171.