基于分支回溯的NAE-3SAT问题求解算法

谷文祥，傅琳璐，周俊萍，姜蕴晖

(1.东北师范大学计算机科学与信息技术学院，吉林长春130117;2.长春建筑学院基础教学部，吉林长春130607)

可满足性问题(satisfiability，SAT)作为计算机理论与应用的核心问题，在智能规划、机器视觉、逻辑推理机以及电子设计自动化等领域中有着重要的理论研究与实际应用价值［1-4］.SAT问题的计算复杂性是NP完全的［5］，这意味着如果P≠NP成立，则无法在多项式时间内解决SAT问题.这时从理论上分析该问题在最坏情况下的时间复杂性上界尤为重要，因为此时对该问题上界的一个微小的改进，例如从O(ck)改进为O((c－ε)k)就会使得问题求解的算法在效率上获得指数级别的提高.多年来，研究人员不断改进SAT问题及其约束子问题的求解算法在最坏情况下的时间复杂度上界［6-11］.以3SAT问题为例，最初Monien和Speckenmeyer在文献［6］中给出了求解3SAT问题的上界为O(2m/3)，其中m是命题公式中的子句数目，目前获得的最好上界为O(1.234m)［8］.SAT 问题理论上的不断发展使得其系统的求解能力有了很大的提高.目前Zchaff、Survey Propagation等SAT求解系统已可以求解包含100 000个以上变量的SAT问题实例［12-14］.

NAESAT(not-all-equal satisfiability)问题作为SAT问题的一个重要扩展，判断是否存在一组真值赋值使得给定的命题公式为可满足，并且使公式的每个子句中所有文字的取值不全为真.NAESAT和NAE-k-SAT(即公式中所有子句的长度都小于等于k，k≥3)都是 NP 完全问题［15-17］，其在集合分裂、最大割集等问题中都有着重要的应用［16］.近来，从理论上研究NAESAT问题及其约束子问题在最坏情况下的时间复杂度上界受到了广泛的关注.Monien等提出NAESAT问题可在O(1.587m)时间内求解，其中m为公式中的子句数目［18］.Riege等将NAESAT问题算法在最坏情况下的时间复杂度上界改进为 O(1.522 8m)［19］.2010 年，Shi等则运用生物学方法提出了一种基于DNA的NAE-3SAT求解算法［20］.

事实上，算法的时间复杂度是根据问题实例的大小计算所得.而对于涉及命题公式的问题，问题实例的大小不仅依赖于公式中子句的数目，还依赖于变量的数目.以变量数目为参数研究NAESAT问题及其约束子问题在最坏情况下的时间复杂度上界，不仅可以从另一个角度衡量算法的好坏，而且在某种程度上更能准确地反映出算法的性能.本文正是以此为着眼点，从变量数目的角度探讨NAE-3SAT问题在最坏情况下的时间复杂度上界，提出了一个基于分支回溯(DPLL)的精确算法NAE.该算法给出了多种化简规则，证明该算法在最坏情况下的时间复杂度上界为O(1.618n)，其中n为公式中的变量数目.

1 基本概念

文中符号 x，y，z…表示布尔变量;符号 l，l1，l2…表示文字.符号 C，C1，C2…表示子句.符号 F，F1，F2…表示CNF公式.

定义1 布尔变量.布尔变量(简称变量)取值为{true，false}.布尔变量x的度 φ(x)为变量x在公式中出现的次数.把在公式中只出现一次的变量称为singleton.

定义2 真值赋值.设变量集合X={x1，x2，…，xn}，定义在变量集合X上的真值赋值是一个函数μ:X→{true，false}.在变量集合X上存在2n组不同的真值赋值.文中把真值赋值简称为赋值.

定义3 文字.设x是一个变量，则称x和¬x为文字，其中称x是正文字，¬x是负文字.当且仅当变量x赋值为true，正文字x在赋值μ下取真值;当且仅当变量x赋值为false，文字¬x在赋值μ下取真值;当且仅当F中恰好包含i个文字l，文字l称为i-文字;当且仅当公式F中恰好包含i个文字l和j个文字¬l，文字l称为(i，j)-文字.公式中已经被赋值为true(false)的文字称为true(false)文字.

定义4 子句.子句由一组文字的析取而成，如C=l1∨l2∨ … ∨lk.当且仅当C中至少有一个文字取值为true，子句C在赋值μ下为可满足.子句的长度是指子句中文字的个数，用符号|C|表示.把长度为k的子句称为k-子句，长度为0的子句称为空子句，用empty表示.空子句为不可满足.

定义5 合取范式.合取范式(conjunctive normal form，CNF)由一组子句的合取而成，如F=C1∧C2∧ … ∧Ci.CNF范式也称为公式F.当且仅当F中每一个子句都为可满足，公式F在赋值μ下为可满足，空公式为可满足.

定义6 NAESAT问题.NAESAT问题对于一个给定的命题公式F，判断是否存在一组赋值使得公式F为可满足并且使公式F的每个子句中所有文字的取值不全为真，即要求公式F的每个子句中至少有一个文字为真，至少有一个文字为假.如果存在这样的一组赋值，则称公式F为NAE-可满足的，否则称公式F为NAE-不可满足.使得公式F为NAE-可满足的赋值称为该公式的NAE-可满足赋值.

如果给定的命题公式F中所有子句长度都小于等于3，则判断是否存在一组赋值使得公式F为可满足并且使公式F的每个子句中所有文字的取值不全为真的问题称为NAE-3SAT问题.

另外需要说明的是，在文中符号F［x/false］表示将公式F中的x赋值为false，相应地¬x赋值为true后得到的子公式;符号F［x/¬y］表示替换x=¬y，即将公式F中的x用¬y替换，¬x用y替换后得到的子公式;符号F［z/y，t/¬y］则表示替换z=y和t=¬y，即同时将公式F中的z用y替换，t用¬y替换，并相应地将¬z用¬y替换，¬t用y替换后得到的子公式.

2 算法NAE

2.1 化简规则

在求解NAE-3SAT问题时，使用化简规则对公式进行约简.应用化简规则的目的是减少公式中的变量数目，缩小搜索空间，提高算法的效率.

规则1:若公式F中存在1-子句，则进行如下化简:

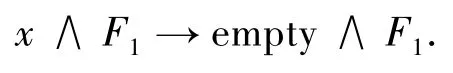
规则2:若公式F中存在2个相同的子句，则进行如下化简:

规则3:若公式F中存在包含重复变量的子句，则进行如下化简:

1)(x∨x)∧F1→empty∧F1;

2)(x∨¬ x)∧F1→F1;

3)(x∨x∨x)∧F1→empty∧F1;

4)(x∨x∨¬ x)∧F1→F1;

5)(x∨¬ x∨y)∧F1→F1;

6)(x∨x∨y)∧F1→F1［y/¬ x］;

7)(true∨x∨x)∧F1→F1［x/false］;

8)(false∨x∨x)∧F1→F1［x/true］;

9)(true∨x∨¬ x)∧F1→F1;

10)(false∨x∨¬ x)∧F1→F1.

规则4:若公式F中存在2-子句，则进行如下化简:

1)(false∨false)∧F1→empty∧F1;

2)(true∨true)∧F1→empty∧F1;

3)(false∨true)∧F1→F1;

4)(false∨x)∧F1→F1［x/true］;

5)(true∨x)∧F1→F1［x/false］;

6)(x∨y)∧F1→F1［y/¬ x］.

规则5:若公式F中存在包含2个或以上true或false文字的3-子句，则进行如下化简:

1)(false∨false∨false)∧F1→empty∧F1;

2)(true∨true∨true)∧F1→empty∧F1;

3)(false∨true∨false)∧F1→F1;

4)(false∨true∨true)∧F1→F1;

5)(true∨true∨x)∧F1→F1［x/false］;

6)(false∨false∨x)∧F1→F1［x/true］;

7)(false∨true∨x)∧F1→F1.

规则6:若公式F中存在包含1个true或false文字和singleton的3-子句，则进行如下化简:

1)(true∨x∨y)∧F1→F1;

2)(false∨x∨y)∧F1→F1.

其中x或y为singleton或者x、y是singleton.

规则7:若公式F中存在包含2个或以上的singleton的3-子句，则进行如下化简:

其中 x、y、z或者 x、y是 singleton.

规则8:若公式F中存在2个子句，它们包含的变量都相同，则进行如下化简:

1)(x∨y∨z)∧(x∨y∨ ¬z)∧F1→F1［y/¬ x］;

2)(x∨y∨z)∧(x∨¬y∨¬z)∧F1→F1［y/¬ z］;

3)(x∨y∨z)∧(¬ x∨¬ y∨¬ z)∧F1→(x∨y∨z)∧F1.

化简规则的执行时间均为多项式时间.一旦某个规则的条件满足，该规则就可被执行，且所有规则按照顺序依次执行，即后面的规则只有在前面的规则都不适用时才会被执行.待处理的公式F重复地被以上8条规则化简，直到所有规则的条件都不满足为止.

定理1 以上8条化简规则都是正确的，不会影响算法对公式F的NAE-可满足性的判断.

证明 由NAE-3SAT问题的定义可得规则1～5是正确的.在化简过程中，把NAE-可满足的子句直接从公式中消去，把NAE-不可满足的子句赋为空子句，即empty.

规则6化简包含一个true或false文字和singleton的子句，因为对singleton的赋值不影响公式中其他变量的取值，可直接把singleton赋值为false(规则6中1))或true(规则6中2))使子句为NAE-可满足.因此可直接把该子句从公式中消去.规则7与规则6类似.

在规则8的1)中，假设公式F包含2个子句为(x∨y∨z)和(x∨y∨¬ z)，如果 y=x=true 或 y=x=false，则2个子句中肯定有一个是NAE-不可满足，所以必须使y=¬x;规则8中2)与规则8中1)类似;规则8中3)，2个子句的文字皆为互补，由NAE-3SAT问题的定义可得若存在一组赋值使得其中一个子句为NAE-可满足，则该赋值肯定也能使另一个子句为NAE-可满足，所以可消去其中一个子句.因此规则8是正确的.

综上所述，8条化简规则都是正确的，化简过程不影响公式的可满足性，即若化简后的公式F'∈NAE-3SAT，则可判定原公式F∈NAE-3SAT.

化简后公式中将不存在1-子句、2-子句、包含重复变量的子句、包含2个或以上true或false文字的3-子句、包含1个true或false文字和singleton的3-子句、包含2个或以上的singleton的3-子句，且不会存在2个包含3个相同变量的3-子句.

2.2 NAE 算法框架

算法NAE的基本思想是给定任意的3-CNF公式F，首先利用2.1节中的化简规则对公式进行简化;然后在化简后的公式中选取某些变量进行分支，分别判断各个分支的NAE-可满足性，进而判断出原公式的NAE-可满足性;递归地执行这个过程直到公式为空或者判定公式为NAE-不可满足后停止.

算法的输入是一个待处理的3-CNF公式F，输出为true或者 false，true表示公式 F为 NAE-可满足，false表示公式F为NAE-不可满足.下面给出了算法的基本框架.

算法 NAE(F).

输入:A formula F in 3-CNF.

输出:If F is NAE-satisfiable，return true;

Else，return false.

1)Apply the rule 1～8 to F as long as one of them is applicable.

2)If F is empty，return true.

3)If F contains an empty clause，return false.

4)If F contains a clause with one true or false literal，C1=true∨x∨y or C1=false∨x∨y，then return(NAE(F［x/y］)∨NAE(F［x/¬ y］)).

5)If F contains two clauses C1=(x∨y∨z)，C2=(x∨y∨t)，then return(NAE(F［x/y］)∨NAE(F［x/¬ y］)).

6)If F contains two clauses C1=(x∨y∨z)and C2=(x∨¬ y∨t)，then return(NAE(F［x/y］)∨NAE(F［x/¬ y］)).

7)If F contains two clauses C1=(x∨y∨z)and C2=(¬ x∨¬ y∨t)，return(NAE(F［x/y］)∨NAE(F［x/¬ y］)).

8)Else choose a clause C1=(x∨y∨z)，return(NAE(F［x/y］)∨NAE(F［x/¬ y］)).

9)End.

定理2 算法NAE能正确地判断一个3-CNF公式是否为NAE-可满足.

证明 下面的证明过程将对算法的每一行进行分析.

算法首先对公式F进行化简(第1步)，当所有化简规则都不可用时，进行判断:因为在化简过程中将NAE-可满足的子句直接从公式中消去，所以若化简后的公式F为空，则说明公式为NAE-可满足，返回true(第2步);因为在化简过程中将NAE-不可满足的子句赋为空子句，所以若化简后公式F包含空子句，则说明公式为NAE-不可满足，返回false(第3步).

若化简后的公式F既不为空也不包含空子句，则算法进入分支过程(第4～9步).分支过程根据化简后的公式分几种情况进行:第4行:考虑公式中存在true或false文字的情况.由定理1可知包含该文字的子句一定为 C1=(true∨x∨y)或 C1=(false∨x∨y)，其中 x、y 为非 singleton.不失一般性，假设子句C1=(true∨x∨y)并对C1进行分支，分别判断2 个子公式 F［x/y］和F［x/¬ y］的 NAE-可满足性，只要其中一个为NAE-可满足，则可说明原公式为NAE-可满足;第5～7步:考虑公式中存在2个子句包含2个相同变量的3种情况.对每一种情况，都进行分支，分别判断2个子公式F［x/y］和F［x/¬y］的NAE-可满足性;第8步:若以上情况都不存在，则公式中的任意2个子句间至多包含一个相同变量，算法任意选择公式中的一个子句进行分支，分别判断 2 个子公式 F［x/y］和 F［x/¬ y］的 NAE-可满足性.

综上所述，算法NAE是正确并且完备的，能正确判断一个给定的3-CNF公式是否为NAE-可满足.

3 算法NAE时间复杂性分析

在本节中，用分支树的方法来分析算法NAE的时间复杂性，并证明了其在最坏情况下的时间复杂度上界为O(1.618n)，其中n为公式中的变量数目.首先给出分支树的概念.

分支树是一个由i(i＞0)个结点组成的集合T，是一棵层级结构树［21-22］.分支树的每个结点标记一个CNF公式，其中一个特定的结点为根结点，标记为公式F，除根结点外的其他结点被划分为j(j≥0)个互不相交的有限集合T1，T2，…，Tj，每一个集合又都是分支树，称为根的子分支树，分别标记为公式F1，F2，…，Fj.公式 F1，F2，…，Fj是对公式F 中的某些变量进行赋值后得到的公式，为公式F的子公式.分支树的叶子结点标记的是空公式或者包含空子句的公式.

分支树中的每一个结点都有一个分支向量.设分支树中某一个结点是F0，它的子结点分别是F1，F2，…，Fk，则结点 F0的分支向量为 τ(r1，r2，…，rk)，其中 ri=f(F0)－f(Fi)，f(Fi)(0≤i≤k)是公式Fi中变量的数目.每个结点所对应的分支向量的值称为该结点的分支数，可用式(1)计算:

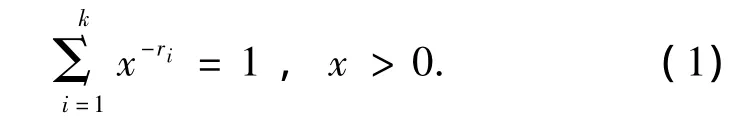
所有结点分支数中最大的被定义为分支树的分支数，用符号τmax表示.

定理3［7］设分支树T的根结点标记为公式F，则分支树T中叶子的个数不超过(τmax)n，n是公式F中变量的数目.

因为分支树的构造过程相当于基于分支回溯算法的执行过程，它们逐一地对公式F中的变量进行赋值，直到确定公式的可满足性为止.所以可用分支树的方法对基于分支回溯的算法进行时间复杂性的分析.假设算法在分支树T中任意一个结点执行的操作都是多项式时间，那么算法的执行时间t为

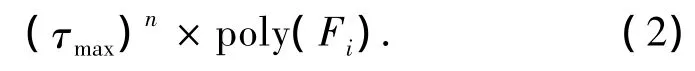
式中:符号#{Tnode}表示分支树T中结点的个数，符号#{Tleaves}表示分支树T中叶子结点的数目，符号ploy(Fi)表示每个结点操作所用的时间是多项式时间.在本文中，忽略多项式时间.

定理4 算法NAE在最坏情况下的时间复杂度上界为O(1.618n)，其中n为公式中变量的数目.

证明 下面将对算法NAE的每一行进行时间复杂度分析.

第1～3步:多项式时间内时间复杂变为O(1).

第4步:不失一般性，假设子句C1=true∨x∨y.在分支 F［x/y］中 C1=(true∨y∨y)，由化简规则3中7)可得，y=false，因此消去x、y 2个变量.在分支F［x/¬ y］中 C1=(true∨¬ y∨y)，由化简规则 3中9)可得子句C1可直接消去，因此消去x一个变量.执行时间为O(τ(2，1)n)=O(1.618n).

第5步:在分支 F［x/y］中子句 C1=(y∨y∨z)，C2=(y∨y∨t)，由化简规则 3 中 6)可得，z=t=¬ y，消去 x、z、t 3 个变量.分支 F［x/¬ y］中 C1=(¬ y∨y∨z)，C2=(¬ y∨y∨t)，由化简规则 3 中5)可得子句C1、C2可直接消去，消去x一个变量.执行时间为O(τ(3，1)n)=O(1.466n).

第6步:在分支F［x/y］中由化简规则3中5)和6)可得，z=¬y，消去 x、z 2个变量.同理在分支F［x/¬ y］中可消去 x、t 2 个变量.执行时间为O(τ(2，2)n)=O(1.414n).

第7步:在分支F［x/y］中由化简规则3中6)可得，z= ¬ y，t=y，消去 x、z、t 3 个变量.在分支F［x/¬ y］中由化简规则3中5)可得子句 C1、C2可直接消去，消去 x一个变量.执行时间为O(τ(3，1)n)=O(1.466n).

第8步:在分支F［x/y］中由化简规则3中6)可得，z= ¬ y，消去 x、z 2 个变量.在分支 F［x/¬ y］中由化简规则3中5)可得子句C1可直接消去，消去 x一个变量.执行时间为 O(τ(2，1)n)=O(1.618n).

由以上分析可得，算法NAE最坏情况下的时间复杂度上界为O(1.618n).

4 结束语

本文从变量规模的角度探讨了NAE-3SAT问题在最坏情况下的时间上界.针对NAE-3SAT问题新提出的8条化简规则有效地提高了算法的时间效率.对于算法时间复杂性的分析，本文采用的是标准测度.近年来，众多学者也在采用非标准测度来分析算法的时间复杂性，如measure and conquer方法.后续的工作将考虑利用非标准测度来分析算法的时间复杂性.

［1］COLMERAUER A.Opening the Prolog III universe［J］.Byte Magazine，1987，12(9):177-182.

［2］KLEER J.Exploiting locality in a TMS［C］//Proceedings of the 8th National Conference on Artificial Intelligence.Boston，USA，1990:264-275.

［3］GU J.Local search for satisfiability(SAT)problem［J］.IEEE Transactions on Systems， Man and Cybernetics，1993，23(4):1108-1129.

［4］李未，黄文奇.一种求解合取范式可满足性问题的数学物理方法［J］.中国科学:A辑，1994，24(11):1208-1217.LI Wei，HUANG Wenqi.A mathematic physical approach to the satisfiability problems［J］.Science in China:Series A，1994，24(11):1208-1217.

［5］COOK S A.The complexity of the theorem-proving procedures［C］//Proceedings of the Third Annual ACM Symposium on Theory of Computing.New York，USA，1971:151-158.

［6］MONIEN B，SPECKENMEYER E.Upper bounds for covering problems［R］.Universitat-Gesamtho Chschule-Paderborn:Reihe Theoretische Informatik，1980.

［7］HIRSCH E A.New worst-case upper bounds for SAT［J］.Journal of Automated Reasoning，2000，24(4):397-420.

［8］YAMAMOTO M.An improved O(1.234m)-time deterministic algorithm for SAT［J］.Lecture Notes in Computer Science，2005，3827:644-653.

［9］MONIEN B，SPECKENMEYER E.Solving satisfiability in less than 2n steps［J］.Discrete Applied Mathematics，1985，10(3):287-295.

［10］BRUEGGEMANN T，KERN W.An improved local search algorithm for 3-SAT［J］.Theoretical Computer Science，2004，329(1/2/3):303-313.

［11］DANTSIN E，GOERDT A，HIRSCH E A，et al.Adeterministic(2-2/(k+1))n algorithm for k-SAT based on local search［J］.Theoretical Computer Science，2002，289(1):69-83.

［12］ZHANG Lintao，MADIGN C F，MOSKEWICZ M H，et al.Efficient conflict driven learning in a Boolean satisfiability solver［C］//Proc of the ACM/IEEE ICCAD 2001.New York，USA，2001:279-285.

［13］ZECCHINA R，MEZARD M，PARISI G.Analytic and algorithmic solution of random satisfiability problems［J］.Science，2002，297(5582):812-815.

［14］ZECCHINA R，MONASSON R，KIRKPATRICK S，et al.Determining computational complexity from characteristic phase transitions［J］.Nature，1999，400(6740):133-137.

［15］THOMAS J S.The complexity of satisfiability problems［C］//Conference Record of the Tenth Annual ACM Symposium on Theory of Computing.New York，USA，1978:216-226.

［16］PORSCHEN S，RANDERATH B，SPECKENMEYER E.Linear time algorithms for some not-all-equal satisfiability problems［C］//Proceedings of the 6th International Conference on Theory and Application of Satisfiability Testing(SAT2003).Santa Margherita Ligure，Italy，2003:172-187.

［17］WALSH T.The interface between P and NP:COL，XOR，NAE，1-in-k，and Horn SAT［C］//Eighteenth National Conference on Artificial Intelligencet.Edmonton，Canada，2002:685-700.

［18］MONIEN B，SPECKENMEYER E，VORNBERGER O.Upper bounds for covering problems［J］.Methods of Operations Research，1981，43:419-431.

［19］RIEGE T，ROTHE J，SPAKOWSKI H.An improved exact algorithm for the domatic number problem［J］.Information Processing Letters，2006，101(3):101-106.

［20］SHI Nungyue，CHU Chihping.A DNA-based algorithm for the solution of not-all-equal 3-SAT problem［C］//ASE International Conference on Information Engineering.Taiyuan，China，2009:94-97.

［21］ZHOU Junping，YIN Minghao，ZHOU Chunguang.New worst-case upper bound for#2-SAT and#3-SAT with the number of clauses as the parameter［C］//Proceedings of 24rd AAAI Conference on Artificial Intelligence.Atlanta，USA，2010:217-222.

［22］周俊萍，殷明浩，周春光，等.最坏情况下#3-SAT问题最小上界［J］.计算机研究与发展，2011，48(11):2055-2063.ZHOU Junping，YIN Minghao，ZHOU Chunguang，et al.The worst case minimized upper bound in#3-SAT［J］.Journal of Computer Research and Development，2011，48(11):2055-2063.