一种五轴机床检验试件轮廓误差的处理与显示技术研究*

丁杰雄，谭 阳，崔浪浪，赵 波，王 伟

(电子科技大学机械电子工程学院，成都 611731）

0 引言

数控机床加工，尤其是五轴联动数控机床加工作为一种先进的制造方法，在现代加工中有着越来越广泛的应用。数控机床出厂安装、调试和后续生产、维护、维修都需要对其加工精度进行测评，机床的加工性能直接反映在工件精度上。评价机床加工精度，其中一个有效的方法是试切机床检验试件，检验试件的精度可以直接反映机床加工精度和性能。

国家标准中规定机床检验试件分用户试件和标准试件［1］。用户试件是由机床使用者提供的面向加工零件的检验试件，标准试件是机床行业使用的面向机床本身的检验试件。

美国宇航局(NASA）在1969年提出了NAS979试件对数控机床进行综合检测［2］，如图1所示。作为一种机床检验标准试件，在数控机床行业得到了普遍的认同和广泛应用。

图1 NAS979试件

NAS979试件由孔、正方形、菱形边界和3度倾斜的四方形组成综合体，NAS979在美国波音公司的航空件制造中被要求强制推行。通过基于NAS979试件切削的一系列12项测试，可以综合反映出机床加工的最大扭矩、最大功率、最大进给步长、过切、欠切、运动精度、重复性和加工精度等。

针对飞机结构件加工特点，中航工业成都飞机工业公司提出了一种S形机床检验标准试件，并申请了美国专利［3］。它是由给定的离散点通过样条插值，作为试件的上下边界，再通过扫掠的方法构造出直纹面，如图2所示。它的设计表达了航空件的薄壁特性，可以考察多轴机床工作时开、闭角的转换，在航空制造业中得到了一定的推广。

图2 S试件

对于检验试件型面精度的测量，通常由三坐标测量仪完成。三坐标测量仪的测试报告能给出测试点相较于理论值的法向误差，但当测试点较多时，则不便于生产人员快速判断检验试件的加工质量。本文研究一种利用数学分析软件Matlab对S形检验试件进行轮廓误差处理与显示的技术，分别运用了曲线样条插值和平面线性插值的方法，对理论曲面进行重构以及再加入三坐标测量仪测试的型面误差数据后，得到实际S试件的误差分布三维图形，并对误差进行数据分析。通过型面构造和型面误差的可视化，较直观的反映出机床加工精度和性能。

1 S形检验试件曲面分析及重构

1.1 检验试件曲面特点

S试件如图3所示，可分为大致左右对称的7个区域:1、7区域是试件的两端，在XOY面单调递增，且斜率很大;2、6区域单调递减，且斜率绝对值很大，与前后区域衔接处出现X方向反向;3、5区域为平滑弧线，考验机床动态跟踪性能，且该区域出现Y方向的反向;加工4区域时，刀具会出现开闭角的转换。

S试件厚度为3mm，属于薄壁件，刚度小，对振动敏感，需要小进给量，高速加工，对机床刚度要求高。

1.2 样条插值重构曲线

对S试件上下边界进行重构。由给定的50个空间点组成的点集，每个点由x，y，z三个坐标表示。对曲线的插值采用三次样条插值，这种方法克服了分段三次埃尔米特插值的弱点，它只需要在插值区间端点比拉格朗日插值多两个边界条件，就可以构造出插值函数，而且这类插值函数在插值节点处具有二阶导数连续，从而具有更好的光滑性。样条插值的思想来源于工程实际问题，而它成熟的数学方法又在工程实际中得到广泛应用［4］。

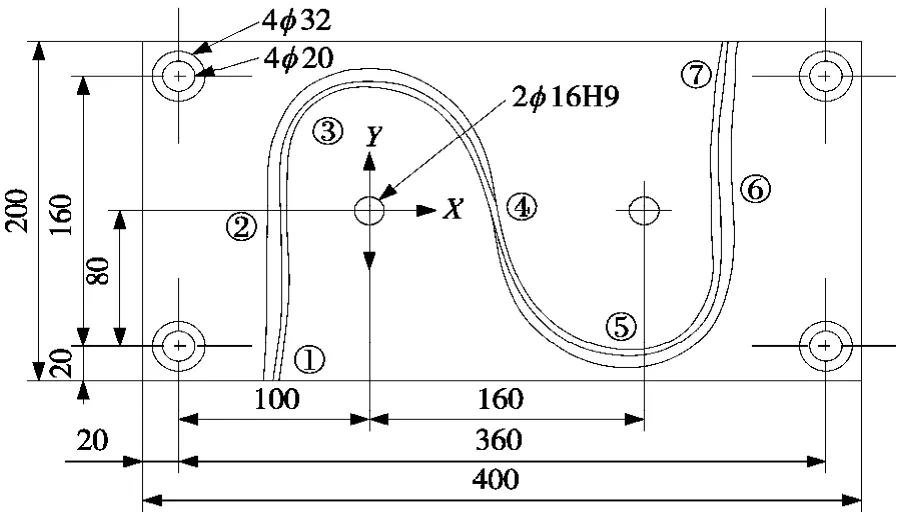
图3 S试件俯视图

三次样条曲线是由多段三次多项式曲线光滑拼接而成，相邻段之间端点处的一阶导数与二阶导数相同。设平面上有n个节点，表示为式(1）:

并且相邻样条曲线节点处的一阶导数和二阶导数相等，如式(3）所示:

在满足上面条件的情况下，再增加边界条件，用待定系数法可依求出n个分段三次多项式，把这n个分段多项式统称为该问题的三次样条插值函数。限定两端切线方向，给定两端切向量。认定曲线在第1段与最后一段(n-1段）为抛物线，即这两段曲线的二阶导数为常数，让端点处的二阶导数为?［5］。

将S试件原始点位数据载入Matlab，共两组数据，每组50个点，每个点由X，Y，Z三个坐标值表示，相邻点之间直线距离为13.65mm左右，作为曲线显示间隔偏大，需通过插值密化显示点。

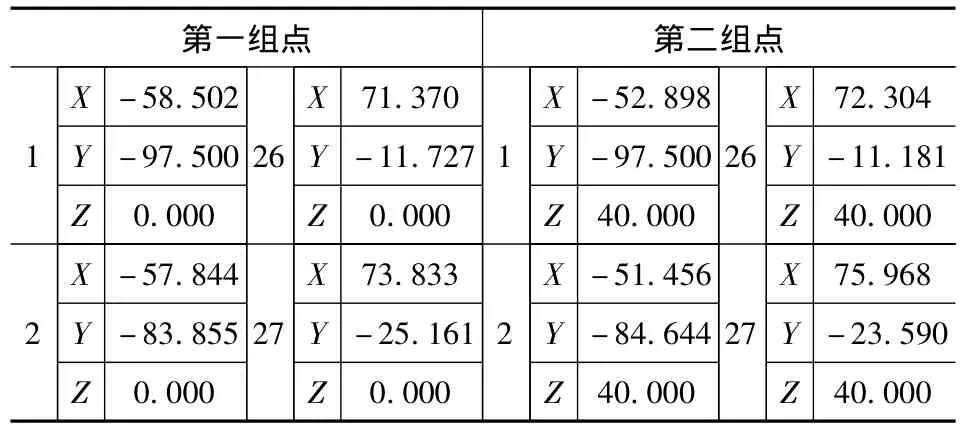
表1 S试件部分原始点位数据

spline函数就是Matlab中三次样条插值的函数名。运用此函数将第一组点位数据载入，结果如图4所示。

可以看出插值效果不好，图中小圆点为插值节点，在S试件的2356区域出现了很大振荡。出现这一情况的原因是，S件1，2，6，7区域在x方向不单调且斜率趋近于无穷，而式(1）中的限制条件x1＜x2＜…xn，要求插值节点应单调递增。通过计算机的数值插值计算，出现了图形的剧烈跳动。

图4 下边界样条插值效果图

1.3 分段线性插值重构曲线

针对上述遇到的困难，改用分段线性插值，通过密化插值点位，运用线性插值，以解决曲线振荡问题。类似的，设平面上有n个节点，表示为式(4）:

L(x）表示分段函数，且:

第i段的函数表达式为:

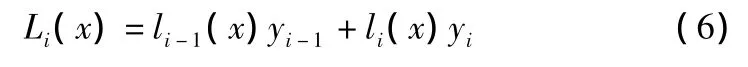
直接采用50个点位分段线性插值，弦高约为0.35mm。增加从S件数字模型上提取的数据点，在200个左右出现拐点。综合精度与计算量两方面因素，在试件顶部和底部轮廓线上各提取225个插值节点进行分段线性插值，较为合适。由于是以直线代替样条曲线，在S件曲率最大的3号区域，将图形放大如图5所示。

图5 S试件底部轮廓线放大对比图

虚线为分段插值的直线，实线为没有振荡现象的样条曲线，可以看到弦高大约为0.05mm。密化后两相邻插值节点间的距离为3mm左右，弦高占节点间距的1.67%，在视觉感受中差别可忽略，因此可将分段插值用作显示的基准轮廓偏差。结果如图6所示。

图6 S试件顶部和底部轮廓线

1.4 三维线性插值重构曲面

类似分段线性插值的方法，通过三维线性插值的方法可对点云数据划分网格，重构三维曲面。这种方式应用较广，一般说来在曲面曲率较大时，点云分布较密集［6］。

由于S试件沿z轴方向曲率变化不大，在S试件的数字模型上采用均匀取点的方式，朝向Y轴负方向的表面上，选取15层，每层按图6均匀选取225个插值节点，对曲面进行重构。每个节点有x，y，z三个坐标值，将点位数据整理成3个225*15的矩阵［xi］，［yi］，［zi］，分别代表所有节点在 x，y，z三个方向的坐标。Matlab提供了绘制阴影曲面的surf函数，构造出的曲面是由很多较小的四边形构成。代码为:surf(xi，yi，zi，ones(225，15））。绘制的 S 试件基准显示型面如图7所示，星号为坐标原点:

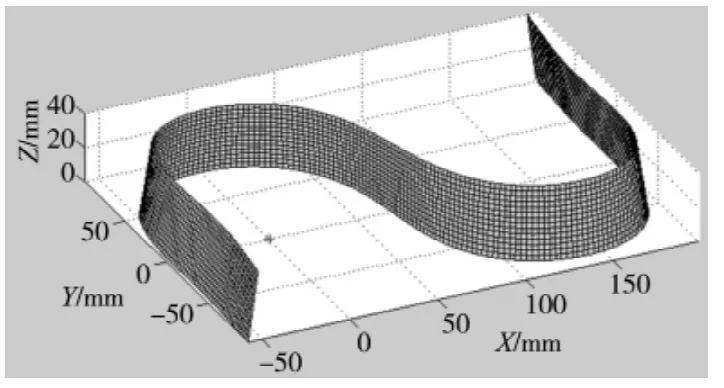
图7 S试件型面网格图

2 基于测试点云的检验试件轮廓误差处理及可视化

2.1 S试件的型面法向误差插值

三坐标测量仪得到的是各测试点相对基准型面的法向误差，测量时需要输入测试点的三维坐标以及测量头的进给方向。考虑到测量机的检测效率，不可能按图7中S型面225*15个节点来测量曲面上每个点的偏差数据，仅需测量重点区域的部分点位，一般选择实际加工中容易出现超差的100个点，其余节点的误差可通过插值的方法来估计。一般情况下，S试件的1，7区域，由于端部属悬臂支撑，刚度小;试件3，5区域的曲率最大;4号区域出现了机床开闭角的转换，在这些区域选择测试点位适当密集些。

根据测试点位的离散误差数据，利用插值方法使其分布在S试件整个表面。为使图7中225*15个节点都有误差，需对法向误差数据进行二维插值。如图8所示设四个插值点(矩形的四个顶点）处的误差值为式(8）:

图8 二维插值原理图

运用Matlab自带的一般分布二维散点数据插值函数，代码如下:ci=griddata(x，y，c，xi，yi，＇v4＇）。其每个参数的含义如下:

ci:每个插值节点插值后的法向误差数据，为一个225*15的矩阵。

griddata:非网格数据插值函数名，由于测量点为离散点，所以用此方法进行插值计算。

(3)运用SVM算法[7]，检索提取的特征向量构成的最优超平面，并以此来构造写作风格分类器，通过利用训练集的数据进行训练，得到作者身份识别模型。

x:测试点x坐标，为一个100*1的矩阵，表示100个测试点的x坐标值。

y:同 x。

c:实际测量100个测试点对应的法向误差。

xi:插值节点x坐标，为一个225*15的矩阵。

yi:同 xi。

＇v4＇:griddata函数中的一种插值方法，其余方法还有＇linear＇、＇nearest＇、＇spline＇、＇cubic＇，分别代表双线性插值、最近邻插值、三次样条插值、双三次插值，＇v4＇代表Matlab4.0提供的非网格数据优化插值算法，公认效果较好。将100个测试点位的法向误差映射到S试件基准型面的225*15个显示节点上，从而形成密化的误差数据。

值得一提的是，上一小节提到的网格重构曲面的方法用于显示试件型面，它会引入微小误差，这种误差表示重构后的型面和理论型面之间的差异，在视觉上这种微小误差是不会影响试件型面的可视化显示的。本小结提到以试件法向误差与重构型面时引入的微小误差不同，它表示通过三坐标测量机测量出的实际零件型面和理论型面之间的法向距离。

2.2 将法向误差分解在坐标轴上的处理方法

为了得到S试件基准型面上的每个节点叠加法相误差后的实际位置，需将每个节点的法向误差投影在x，y，z轴上，与该节点的基准坐标位置进行相加运算。计算图7中试件型面各节点的法向方向。由插值点的前后左右相邻两点与之构成的交叉向量叉乘，法向量n=A×B，原理如图9所示。

图9 求曲面法向原理图

计算结果如图10所示。

图10 S试件节点法向图

根据空间几何平行四边形法则，可求得S试件基准显示型面上每个节点在坐标轴上的投影分量，矩阵［ci］的每个元素分别乘以矩阵［u］［v］［w］的对应元素，得到的矩阵［cx］，［cy］，［cz］即是误差在各坐标轴上的投影。

2.3 等高线方式显示误差

S试件实际点云可以由误差数据加上理论点位坐标数据而来。通过类似等高线的方式可以表示S试件型面。这样的表示方法，可以作为机床加工S试件表面走刀路径的参考，但由于加工误差的数量级为亚毫米级，表示出来很不明显。沈向东针对传统方法检测零件表面的缺点，研究开发出了零件表面检测系统，旨在对超精密加工的零件表面质量进行检测、分析与评价，他将零件表面的三维立体图沿其高度方向上放大了一千倍，而使表面的状态峰谷高度差变得明显，可以清晰地看出零件表面的纹路方向［7］。本文采用类似的方法，将 S试件的误差［cx］，［cy］，［cz］矩阵乘上一个放大系数 10 后，结果如图11所示。

图11 S试件等高线放大误差图

可以看出，S试件型面不再光滑，有明显的凹凸感，配合文字注释，有助于对S试件质量作出快速判断。

2.4 灰度方式显示误差

以等高线的方式表示误差分布，虽然可以快速判断试件表面质量好坏，但无法知道误差的大小，配合灰度比对表以灰度的方式表达试件表面误差的分布，可以解决上述的弊端。这种方法可用于显示误差，也常见于温度场，流速场的绘制中［8］。针对S试件的误差表达，运用灰度对型面网格着色，来区别误差的正负、大小，越亮表示正误差越大，越暗表示负误差越大。配合灰度谱，可以很快的得到试件的误差分布和大致的误差大小，如图12所示。

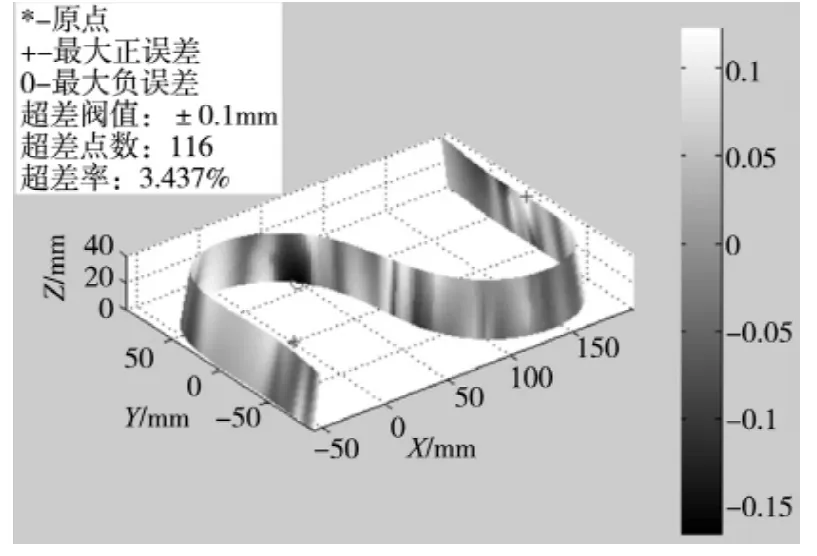
图12 S试件灰度显示误差图

从图中右侧的灰度谱可以判断S试件的误差大都分布在-015mm～+0.1mm之间。

值得一提的是，若以彩色块显示的方式表达型面误差效果更佳，由于文章排版受限，本文以灰度方式显示误差。

2.5 动态图形的输出

以上两种误差显示方法只表示了一个视角的S试件的误差分布，在Matlab中可以通过鼠标旋转观察，但不方便移植在其他平台上。运用Matlab的文件写入函数可以实现gif动态图形格式的输出，可以将S试件的显示制作为旋转的动画。原理是通过设定的图形旋转角度和动画帧数，将每一帧图片写入到指定路径下的gif文件当中。

3 结束语

(1）运用计算机数值计算对S型检验试件上下边界曲线进行样条插值，在曲线不单调的情况下很难得到理想插值结果，并针对这一现象提出了一种针对点云数据分段线性插值的替代方法。

(2）基于数学软件Matlab，针对S形检验试件完成了对其曲面重构和误差分析及误差可视化的工作，对生产加工有重要的意义。并且文中所述的方法能比较容易的运用在其他型面的构造中，具有较强的可移植性。

［1］GB-T17421.1-1998机床检验通则第1部分［S］.

［2］NAS979.Uniform cutting test-NAS series，metal cutting equipment［S］.NAS，USA，1969.

［3］Z.Y.Song，Y.W.Cui.Sshape detection test piece and a detection method for detection the precision of the numerical control milling machine［P］.US，0004777，2010.

［4］钟尔杰，黄庭祝.数值分析［M］.北京:高等教育出版社，2004.

［5］张德丰，赵书梅，刘国希.MATLAB图形与动画设计［M］.北京:国防工业出版社，2009.

［6］Won-Ki Jeong，Kolja Kahler，Jorg Haber，Hans-Peter Seidel.Automatic Generation of Subdivision Surface Head Models from Point Cloud Data［J］.International Graphics Interface 2002 Confence:181-188.

［7］沈向东.精密加工表面粗糙度测量数据分析评价方法的研究［J］.硅谷 SILICON VALLEY，2009(5）:114-115.

［8］Nina Amenta，Marshall Bern，Manolis Kamvysselis.A New Voronoi-Based Surface Reconstruction Algorithm ［J］.SIGGRAPH”98 Proceedings of the 25th annual conference on Computer graphics and interactive techniques:415-421.