生产线上工人分配的两阶段优化模型*

刘绘珍，张毕西，张湘伟，廖朝辉

(郑州航空工业管理学院科学科学与工程学院，郑州 450015）

0 引言

劳动力密集型的生产系统中，工人分配对于系统的效率起着举足轻重的作用。工人的分配问题也受到众多学术界和企业界重视。针对这一问题，本文提出两阶段优化模型。

1 文献研究

Sotirios G.Dimitriadis(2006）［1］采用启发式的方法分配工人到工作站。Yiyo Kuo，Taho Yang(2007）［2］利用混合整数规划的方法对多条生产线多技能工人进行优化分配，目标为最小化工人重叠技能量。Süer and Tummaluri(2008）［3］研究劳动力密集型制造单元中工人的分配问题。考虑工人具有不同的技能水平、学习遗忘率，为多个生产周期分配工人，提出三阶段模型。第一个阶段借助标准操作时间生成每种产品使用工人的数量。第二个阶段确定单元的负荷和单元的大小。第三个阶段分配工人。每个阶段都采用混合整数规划模型。采用两种策略分配工人:Max and MaxMin。Max是最大化生产率，MaxMin是最大化生产率的情况下采用效率低的工人，也就是给不熟练的工人学习的机会。结果显示:Max方法得到最短完工期，Max-Min方法更多提高工人的技水平，Max-Min方法比Max方法更能提高工人的技能水平。Omar Ibrahim Alhawari(2008）［4］在其学位论文中进一步研究Max and MaxMin两个方法，生产环境采用高度动态的劳动力密集型生产环境。该文研究Max and MaxMin如何影响工人的技能水平，完工期和单元的加工时间。制造环境采用有秩序的生产环境，采用相同的产品组合。工人的技能水平考虑学习遗忘。结果显示MaxMin比Max更能提高工人的技能水平。最终也可降低完工期和总的加工时间。刘绘珍等人(2011）［5］研究劳动力密集型制造单元的配置和排序问题。分三阶段解决该问题，依次是:单元配置、人员分配和产品排序。单元配置阶段利用产品的相似性，为单元分配产品。人员分配阶段采用加工时间最长的工序优先分配人员的策略。产品排序阶段采用经典的Palmer启发式算法。Ceyda Gungor Sen，Gokce Cinar(2010）［6］在工人分配之前，利用模糊层次分析法方法评价工人，再利用最大最小工人绩效的方法和非参数统计法为工人分类，为分配工人提供工人绩效信息。Muh-Cherng-Wu(2006）［7］考虑学习效应对工人进行分配，采用规划的方法以降低外包成本，从而降低外包工人的数量。Bokhorst等人(2004）［8］研究双资源约束系统中不同工人指派方法。重点研究工人岗位调度规则:who-rule规则，即选择工人进行作业的方式。仿真研究结果显示:问题提出的规则对异质工人的双资源约束系统有显著影响。Wallace J.Hopp(2004）［9］从生产线各道工序效率平衡的角度对比研究了能力平衡模型和技能链模型，并在不同调度模式和一定培训技能总人次下，比较了两模型对生产系统性能的影响。Gel，E.S 等人(2006）［10］研究员工掌握不同层次技能对生产系统的影响。Iravani，S.M.R等人(2005）［11］提出结构柔性的概念，用矩阵表示工人和技能之间的关系，用矩阵的特征值衡量生产系统结构柔性，结果显示这种衡量标准优于员工技能总量的标准。Iravani，S.M.R 等人(2007）［12］研究呼叫中心工作人员的交叉培训，构建了共享网络模型，采用最短路径方法进行交叉培训，研究结果显示最短路径标准与结构柔性标准相当。O.Zeynep Ak，sin(2011）［13］提出能力柔性，构建生产系统需求和工人能力之间的关系，以各项技能的能力冗余判断生产系统的柔性，结果显示:能力柔性标准优于结构柔性。Bokhorst和Slomp(2000）［14］构建整数规划模型，分配多技能工人到不同工作站以使系统有效地应对工人的旷工和需求波动。Cesani and Steudel(2005）［15］研究了工人岗位指派和调度问题，采用两种工人指派方法:专业指派(指一个工人指派一台或多台机器）和共享指派(指两个或多个工人指派给一个或多台机器）。也可混合使用两种指派策略，此研究还基于负荷共享、负荷平衡和瓶颈工序进行仿真。结果显示:工人负荷平衡和机器共享的程度对单元的绩效影响很大，同时也指出多技能工人能够提高系统绩效。Serpil Sayin等人 (2007）［16］考虑工人学习的因素提出两阶段指派模型:第一个阶段优化技能集合的效用(即工人总效率）;第二阶段，在第一阶段优化条件下，在最大效用的基础上浮动一定范围，以最大化工人技能的提高为目标指派工人。Gürsel A等人(2009）［17］研究了劳动密集型制造单元的工人指派和产品排序模型。B.L.Song，W.K.Wong，J.T.Fan，S.F.Chan(2006）［18］提出递归算法解决工人分配问题，首先为每道工序计算工人的分配量，再借助工人的具体效率，通过递归算法分配工人到具体的工序上。J.T.Fan，S.F.Chan(2007）［19］继续在原来方法的基础上，提出了工人数量有限时的解决方法。本文在J.T.Fan，S.F.Chan(2006）研究的基础上，提出两阶段模型，结果与原文做了比较分析。

2 两阶段模型

两阶段模型中，第一阶段，根据产品在各道工序的加工时间计算出每道工序分配的工人数量，该阶段不考虑工人之间的差异。第二阶段考虑工人之间的差异，根据工人在各道工序上效率的差异，在第一阶段工人数量的限制下，分配工人到工序上，目标是平衡生产线和提高瓶颈工序上的效率。

2.1 第一阶段——计算各道工序分配的工人数量

根据待分配的工人总量，按照产品对应每道工序的标准加工时间及其需求量，按比例计算各道工序分配的工人数量。根据加工产品种类的多少，生产线可以分为:单一产品生产线和混合产品生产线。本研究分布针对两种类型的生产线进行工人数量的分配。

2.1.1 单一产品线上工人分配的数量

假设生产线只有一种产品。根据待分配的工人总量，按照产品对应每道工序的标准加工时间，按比例计算各道工序需要分配的人数。分配的过程中不考虑人的差异，加工时间越长，分配工人越多，即按照各道工序标准加工时间的比例分配工人［7-8，18］程序流程图如图1所示。

参数如下:J表示工序的总量，I表示待分配工人的总量，spm(j）表示第j道工序标准加工时间。令J=3，I=8，spm=［1.20.61.8］，作为算例 1［7］。计算结果为:第一道工序分配3人，第二道工序分配1人，第三道工序分配4人。

图1 计算工人数量的流程图

2.1.2 混合产品线上工人分配的数量

对于混合产品生产线，同一道工序上不同产品的标准加工时间差别较大，对维持生产线平衡和生产线工人的分配与重分配的影响较大。

工人的工资水平通常与其具有的技能高低和技能数量有关。对于混合产品生产线，若所有工人仅仅具有单一技能，只会做一道工序，则工人的分配是刚性的唯一的。而不同产品在各道工序上加工的标准时间不同，生产线的平衡难以维持，从而降低生产线的效率。当部分工人具有多项技能，可提高生产线的柔性，随着加工产品的不同，可重新分配工人。本文兼顾工人的培训成本和生产柔性，在满足一定生产柔性的前提下，尽量降低多技能工人的数量。

对于混合产品生产线上加工的产品，虽然种类众多，但是一般都能归类为有限的几种标准产品。研究生产线的平衡和效率时，只需考虑满足这几种标准产品。每道工序拥有的工人应该满足下式:

假设nopertion(p，j）表示标准产品p在第j道工序上需求的工人数量，sopertion(p，j）表示标准产品p在第j道工序上的拥有单技能工人数量，mopertion(p，j）表示标准产品p在第j道工序上的拥有多技能工人数量。只有满足1式才能合理分配工人。若左边不满足说明单技能工人过多，需要对该工序拥有的单技能工人进行交叉培训。若右边不满足说明该工序拥有工人太少，增加培训该工序的工人。这些预警均可以为决策者提供有用的信息，合理培训和交叉培训工人。

表1 标准产品在每道工序上需求的工人数量及单技能工人的最大数量

2.2 第二阶段——工人-工序的分配

生产中工人效率之间存在很大差异，并受很多因素的影响，比如熟练程度、情绪、疲劳等，这种差异对生产线的影响很大。根据第一阶段为生产线配置的工人数量，第二阶段在具体分配工人到具体工序时考虑该工人在各道工序的效率。

2.2.1 生产线平衡和瓶颈效率的优化

分配工人到生产线的具体工序时，考虑工人在该工序的效率。目标即考虑生产线的平衡也考虑瓶颈工序的效率。假设中间不设在制品库存，整条生产线上效率即为瓶颈工序的效率。模型如下。

参数:i表示工人，j表示工序，eff(i，j）表示工人i在工序j上的效率(单位时间内的产量）。

决策变量:x(i，j）表示工人i是否分配到工序j上，分配为1，否则为0。

目标函数:

约束条件:

根据表2给出的初始数据，用m程序计算出工人的需求量。再利用表3中工人历史记录中的效率数据。用上面的优化程序进行优化，五个算例中优化的结果如表4。

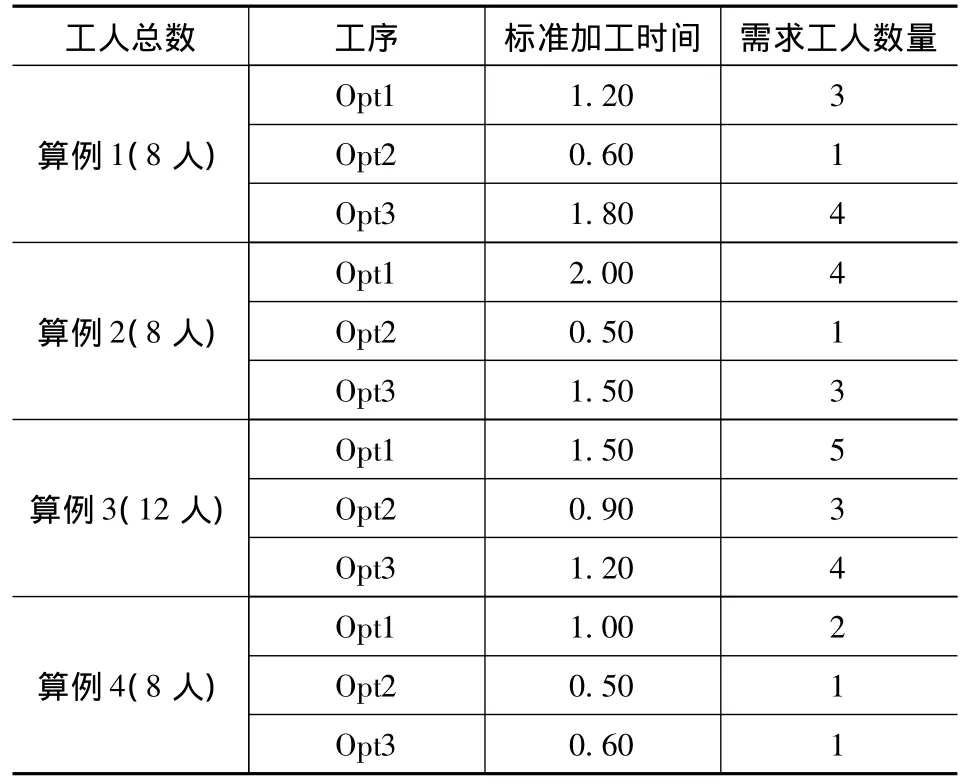
表2 五个算例中初始数据及用m程序计算的工人需求量(注:数据来自文献［18］）

(续表）

表3 五个算例中各道工序对应工人的效率(注:数据来自文献［18］）

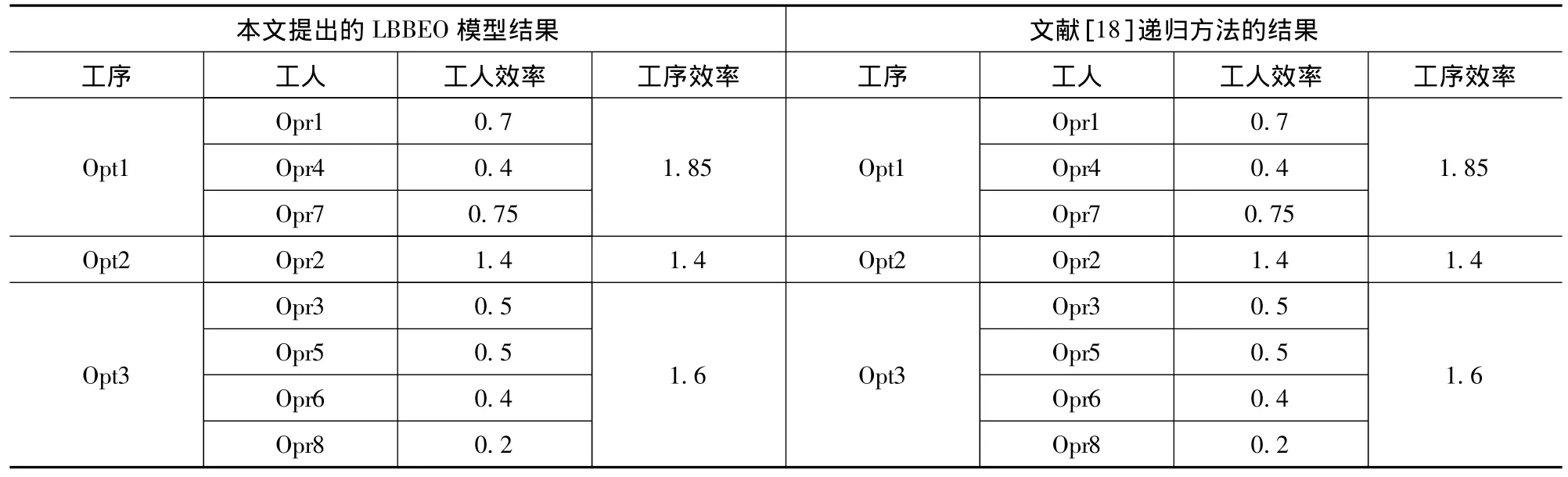
表4 第一个算例优化的结果

表5 第二个算例优化的结果

表6 第三个算例优化的结果

表7 第四个算例优化的结果

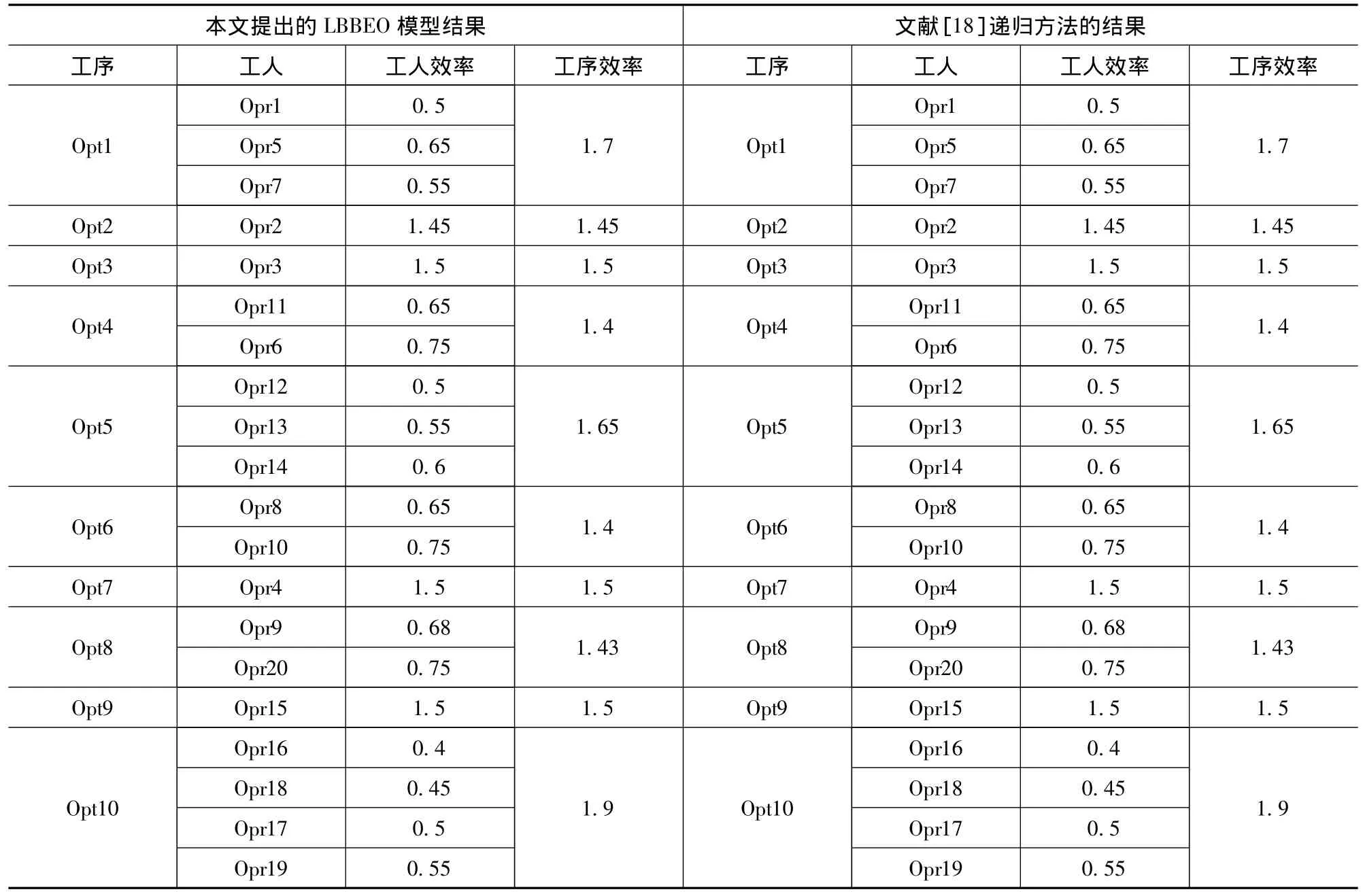
表8 第五个算例优化的结果

表4到表7的数据显示:除了第四个算例外(文献［18］在算例4中计算有误，所以本文不能比较，而比较是该文中给出的企业实际运行数据。结果显示比企业实际运行的数据优，瓶颈工序的效率虽相同，但是从生产线平衡的角度看，本文优化的结果所有工序与瓶颈工序之差的和为1.1，小于企业实际运行数据1.35，所以本文提出的优化结果比企业运行的数据优），其它几个算例都得到同样的结果。文献［18］提出的递归算法比较繁琐，实现起来比较困难，而本文提出0-1规划模型容易理解，并容易用lingo9.0软件实现，软件运行时间小于一分钟。

2.2.2 瓶颈效率的优化

本文还考虑企业运作中，利用有限的人力使产值最大。鉴于该目标，修改2式，由原来既考虑生产线的平衡又考虑效率变为利用有限的人力最大化产值，目标函数改为7式，约束条件和LBBEO模型提出的一样。这样用lingo运行得到的结果和LBBEO模型优化的结果比较，结果显示虽然分配方案有些发生了改变，但所有算例的瓶颈工序效率都没有再增加，这说明五个算例中LBBEO模型优化的结果已经达到了瓶颈工序最大的目的。但仅仅这5个算例也不能说明模型LBBEO和BEO模型的在优化瓶颈工序的效果是相同的，前者是多目标优化，考虑生产线平衡和瓶颈工序的效率。后者是单目标优化，只考虑瓶颈工序的效率。

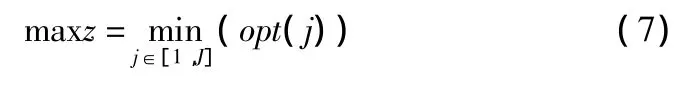
3 结束语

本文采用两阶段模型解决工人的分配问题，和B.L.Song，W.K.Wong，J.T.Fan，S.F(2006）得出的结果基本相同，但方法比较简单，实现起来比较容易。本文提出的两阶段，第一阶段把工人看作同质分配，第二阶段才考虑工人效率的差异。这种方法在工人之间效率差别不大时有效，而工人差异比较大时显然不是最优的方法，这也是后续研究的一个方向。

［1］Sotirios G.Dimitriadis.Assembly line balancing and group working:A heuristic procedure for workers’groups operating on the same product and workstation［J］.Computers＆ Operations Research，2006(33）:2757-2774.

［2］Yiyo Kuo，Taho Yang.Optimization of mixed-skill multi-line operator allocation problem［J］.Computers＆ Industrial Engineering，2007(53）:386-393.

［3］Süer，G.A.，＆ Tummaluri，R.R..Multi-period operator assignment considering skills，learning and forgetting in labour-intensive cells［J］.International Journal of Production Research，2008，46(2）:469-493.

［4］Omar Ibrahim Alhawari.Operator Assignment Decisions in a Highly Dynamic Cellular Environment［D］.The United States of America.The Russ College of Engineering and Technology of Ohio University，2008.

［5］刘绘珍，张湘伟，张毕西，等.劳动密集型制造单元的配置与排序模型［J］. 工业工程，2011，14(6）:27-30.

［6］Ceyda Gungor Sen，Gokce Cinar.Evaluation and pre-allocation of operators with multiple skills:A combined fuzzy AHP and max-min approach［J］.Expert Systems with Applica-tions，2010(37）:2043-2053.

［7］Muh-CherngWu.Shih-Hsiung Sun.A project scheduling and staff assignment model considering learning effect［J］.Int J Adv Manuf Technol，2006(28）:1190-1195.

［8］Bokhorst，A.，Slomp，J.，＆Gaalman，G.(2004）.Assignment Flexibility in a Cellular Manufacturing System-Machine Pooling versus Labor Chaining ［J］.Retrieved from http://www. bdk. rug. nl/organisatie/clusters/PSD/pdf/Faim 2004BokhorstSlompGaalman.pdf.

［9］Hopp，W.J.，Tekin，E.and van Oyen，M.P.Benefits of skill chaining in serial production lines with cross-trained workers［J］.Management Science，2004(50）:83-98.

［10］Gel，E.S.，Hopp，W.J.and van Oyen，M.P.Opportunity of hierarchical cross training in serial production［J］.IIE Trans.2006.

［11］Iravani，S.M，M.P.Van Oyen，and K.T.Sims.Structural flexibility:A new perspective on the design of manufacturing and service operations ［J］.Management Science，2005(51）:151-166.

［12］Iravani，S.M，Kolfal，B.and Van Oyen M.P.Call center labor cross-training:it’s a small world after all［J］.Management Science，2007，53(7）:1102-1112.

［13］Iravani，S.M，Kolfal，B.and Van Oyen M.P.Van Oyen.Capability flexibility:a decision support methodology for parallel service and manufacturing systems with flexible servers［J］.IIE Trans.2011，43(5）:363-391.

［14］Bokhorst，j.and j.slomp.Long-term allocation of operators to machines in manufacturing cells［J］.Group technology/cellular manufacturing world symposium，an Juan，Puerto rico，2000:153-158.

［15］Cesani，V.I.，＆Steudel，H.J.A study of labor assignment flexibility in cellular manufacturing systems.Computers＆Industrial Engineering，2005，48(3）:571-591.

［16］Serpil Sayin，Selc，uk Karabati.Assigning cross-trained workers to departments:A two-stage optimization model to maximize utility and skill improvement［J］.Production，Manufacturing and Logistics.European Journal of Operational Research.2007(176）:1643-1658.

［17］G.A.Suer，F.Arikan，C.Babayigit.Effects of different fuzzy operators on fuzzy bi-objective cell loading problem in labor-intensive manufacturing cells［J］.Computers＆ Industrial Engineering，2009(56）:476-488.

［18］B.L.Song，W.K.Wong，J.T.Fan，S.F.Chan.A recursive operator allocation approach for assembly line-balancing optimization problem with the consideration of operator efficiency［J］.Computers ＆ Industrial Engineering，2006(51）:585-608.

［19］B.L.Song，W.K.Wong，J.Fan and S.F.Chan.An adjusted recursive operator allocation optimization algorithm for line balancing control.IAENG International Journal of Applied Mathematics，2007，36(3）:25-30.