基于差分进化的BP神经网络在纱线质量预测中的应用

曹成辉，黄海涛，王 强

(1.河南工程学院 纺织工程系，河南 郑州 450007；2.方圆标志认证集团山东有限公司，山东 济南 250000)

纱线质量控制是纺织生产中的重要环节，纱线质量的好坏直接影响后面生产工序的进行和最终的产品质量，所以预测纱线的质量特性一直是研究的热点[1].国内外学者采用了许多方法来预测纱线质量，可概括为3类，分别是传统的统计型预测方法[2]、灰色理论预测模型[3]和人工神经网络[4-5]技术.

根据神经元间连接方式的不同,人工神经网络可以分为相互连接网络和分层前馈网络，在纺织领域中应用最广泛的一种是反向传播算法BP神经网络[6].但是，BP神经网络自身也存在着不足[7]，即依赖于初始权值的选择、收敛速度缓慢且容易陷入局部最优.差分进化算法[8](Differential Evolution, DE)是一种基于群体智能理论的优化算法，它具有较强的全局收敛能力和鲁棒性，在神经网络优化[9]、电力、信号处理与经济学等领域得到了广泛应用.

本研究在BP神经网络预测模型中引入了差分进化算法，利用差分进化算法对BP神经网络进行训练，确定了BP神经网络的权值和阈值，解决了BP神经网络收敛速度缓慢且容易陷入局部最优的问题.利用实际数据对纱线质量进行预测实验并与BP神经网络的预测结果进行了对比，结果显示差分进化算法有良好的纱线质量预测性能.

1 基于差分进化的BP神经网络训练算法

1.1 BP神经网络模型

BP神经网络属于前馈型神经网络，具有输入层、隐含层和输出层.根据BP神经网络的设计网络，一般的预测问题都可以通过单隐含层BP神经网络实现[10]，图1为单隐含层BP神经网络模型，其输入层包含m个结点，隐含层包含n个结点，输出层为1个结点.

(1) 输入层到隐含层的权值矩阵W：

(2) 隐含层到输出层的权值矩阵V：

V=[v1，yv2，y…vn，y].

(3) 隐含层的阈值矩阵Z：

(4) 输出层阈值为γ.

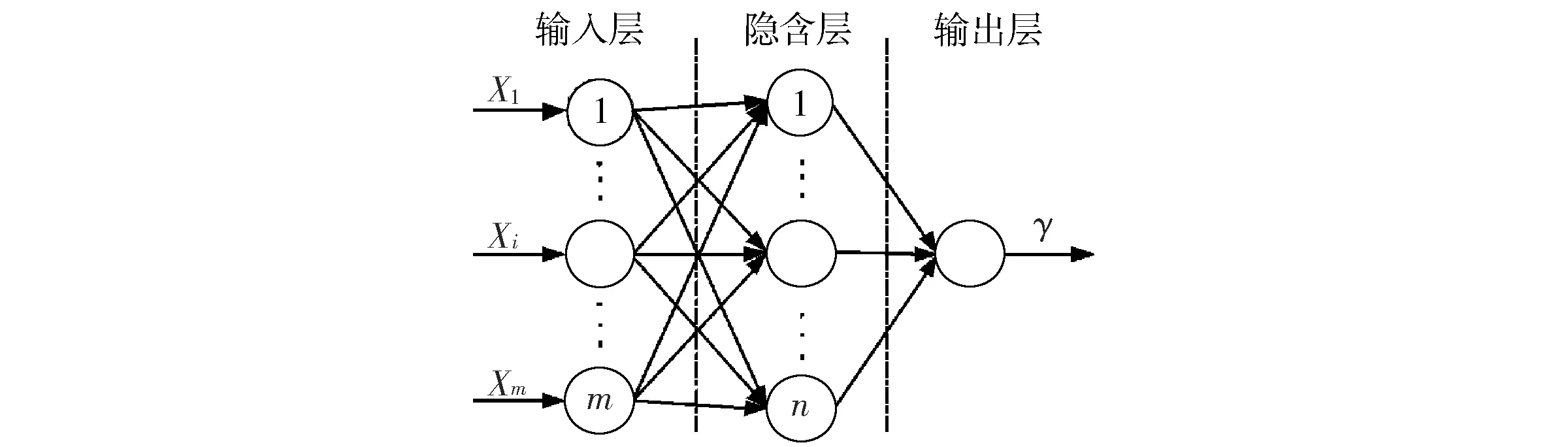
图1 单隐含层BP神经网络模型

1.2 差分进化算法

差分进化算法的本质是一种基于实数编码的具有保优思想的贪婪算法.算法的基本原理是通过把种群中两个个体的向量差加权后，按一定的规划与第三个个体求和来产生新个体，然后将新个体与当代种群中某个预先选中的个体相比较，取适应度值更优的个体作为子代.

1.3 差分进化算法训练BP神经网络

(1)种群初始化

将BP神经网络的3个矩阵W,V,Z和阈值γ映射到差分进化算法的染色体串，映射关系为：{w1，1w1，2…wm，nv1，yv2，y…vn，yz1z2…znγ}.

令R(t)=(R1(t)，R2(t)，…，Ri(t))，其中Ri(t)为第t代种群中第i个个体，Ri(t)={ri1(t)，ri2(t)，…，ril(t)}，i=1，2，…，N；t=1，2，…，tmax，N为种群规模，tmax为最大进化代数，l为染色体长度.

初始化种群R(0)各个体的染色体rij(0)设计变量取其上下边界内随机分布的浮点数.

(2)变异操作

差分进化算法的变异操作基于个体向量差进行.从种群中随机抽取两个不同的个体(Rp1(t)，tp2(t)),按照如下公式进行操作得到新个体：

ui， j(t+1)=rbest，j(t)+η(rp1， j(t)-rp2， j(t))，

(1)

其中,rp1， j(t)-rp2， j(t)是差分向量，rbest， j(t)是第t代适应度最优个体的第j向量，ui， j(t+1)是第t+1代中第i个体的第j向量，η是缩放因子,t=1，2，…，tmax，i=1，2，…N，j=1，2，…l.

(3)交叉操作

为了增加种群多样性，使其不易陷入局部最优，需进行交叉操作.变异后的个体和种群中当前个体Ri(t)进行离散交叉操作，生成个体Xi(t+1).该个体的第j个分量表示如下：

(2)

其中,rand(0，1)是[0,1]范围内的随机小数，rand(i)是[1，i]范围内的随机整数，pc是交叉概率且pc∈(0，1].

(4)适应度函数

适应度函数F是用来评价群体中个体优劣程度的指标,它根据所求问题的目标函数来进行评估,本研究采用下式作为适应度评价函数：

(3)

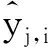
(5)选择操作

对个体Xi(t+1)和个体Ri(t)的适应度值进行比较，若前者的适应度值优于后者，则在第t+1代中用Xi(t+1)取代Ri(t)，否则保留Ri(t),即

(4)

重复执行步骤(2)～(5)，直到连续5代解的差值小于设定误差ε或达到最大进化代数tmax.

2 实验

2.1 实验条件

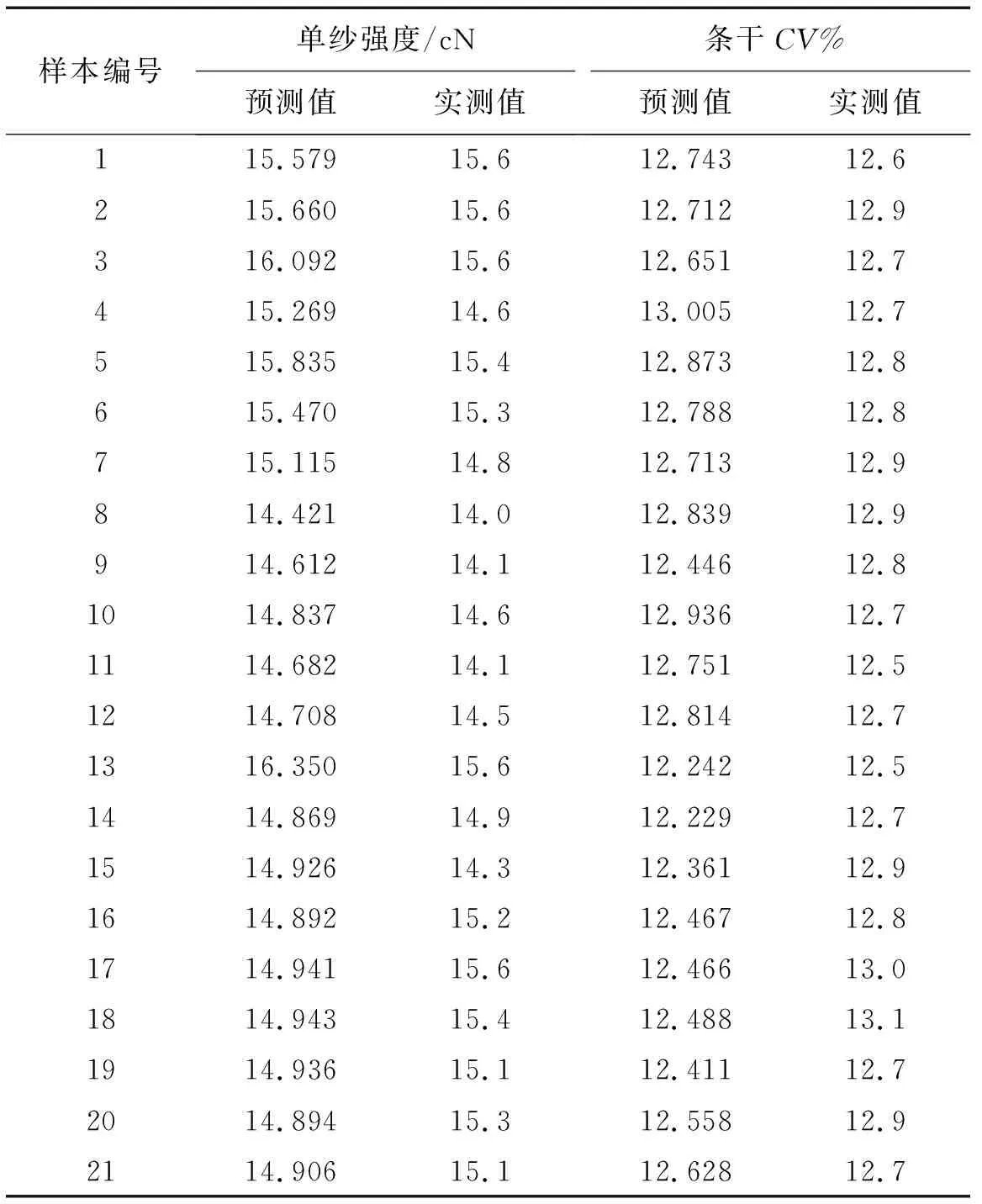
表1 样本预测值与实际值

选用某棉纺厂纺制的J18.2 tex原棉、成纱对照样本56组数据对算法进行检验.选取对成纱质量有显著影响的7项原棉指标作为预测算法的输入项，即含水率、含杂率、主体长度、均匀度、短绒率、成熟度和强力等；选取衡量成纱质量的两项重要指标——单纱强度和条干CV%作为预测的输出项；选取35组数据作为样本进行神经网络训练，采用另外21组数据对算法进行测试.

在Matlab 7.0 环境下进行仿真实验，建立3层BP网络.根据Kolmogorov定理，网络隐含层的神经元为2n+1个[10]，即15个.多次实验也证明此处隐含层神经元数取15时，预测效果最好.设定差分进化算法的种群规模为50，缩放因子η=0.8，交叉概率pc=0.4[11-12].

2.2 实验结果

经过本算法训练的BP神经网络对21组样本数据进行预测，预测值与样本实测值见表1.

将本算法与BP神经网络算法对21组样本的预测误差进行对比，单纱强度预测误差如图2所示，条干CV%预测误差如图3所示.通过图2与图3可知，本算法对成纱质量的预测误差率都在5%以内，优于BP神经网络，可以用来有效地预测纱线质量.

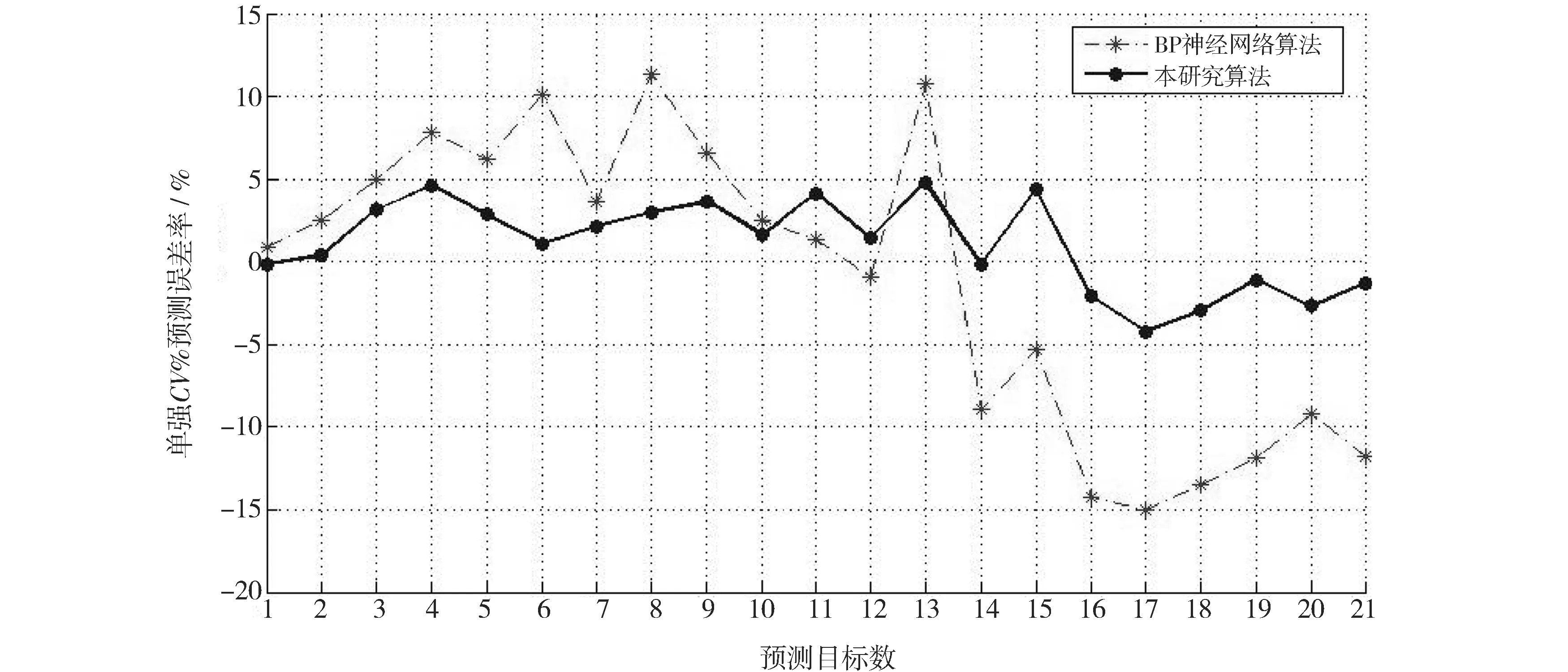
图2 两种算法的单纱强度预测误差率曲线

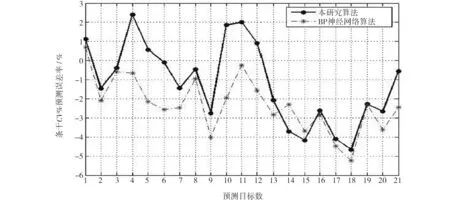
图3 两种算法的条干CV%预测误差率曲线

表2为本研究的算法与BP神经网络算法对21组数据预测得到的最优适应度值，对比可知，无论是单输出预测单纱强度和条干CV%，还是双输出预测单纱强度和条干CV%，本研究算法的适应度值都高于BP神经网络算法.

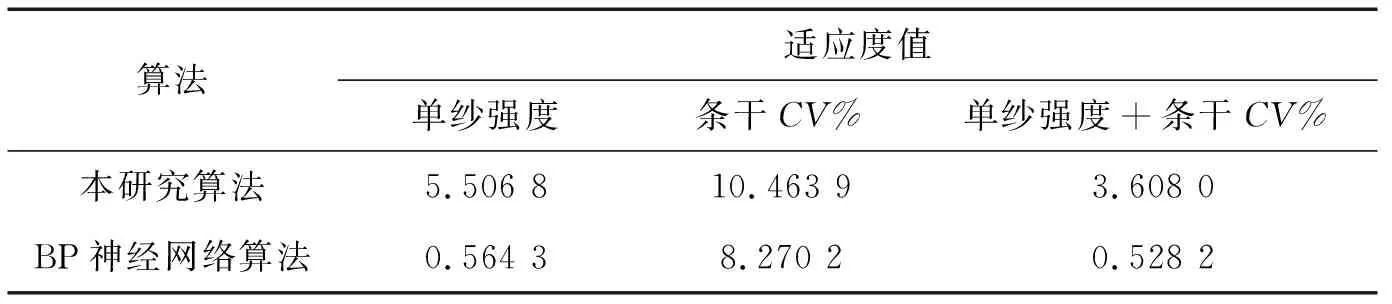
表2 两种算法的测试数据最优适应度值

3 结论

许多研究都表明BP神经网络预测纱线质量是可行的，但预测精度较差.采用差分进化算法训练BP神经网络，优化神经网络的权值和阈值并应用于纱线质量预测，实验对比表明经差分进化算法训练后的BP神经网络在预测精度上有所提高.为了进一步提升BP神经网络的预测能力，应该尽可能增加训练样本数量并对神经网络的结构做更深入的研究.

参考文献：

[1]Reyen M E, Kadoglu H. The prediction of cotton ring yarn properties from AFIS fibre properties by using linear regression models[J].FIBRES & TEXTILES in Eastern Europe,2007,15(4):63-67.

[2]Lloyd B D,Brent S, Waters W T.Analysis of factors influencing ring spun yarn tenacities for a long staple cotton[J].Textile Research Journal,1990,60(8):475-483.

[3]陈东升.用灰色理论预测亚麻成纱质量[J].纺织基础科学学报,1994(3):330-333.

[4]Chattopadhyay R,Guha A,Jayadeva.Performance of neural networks for predicting yarn properties using principal component analysis[J].Journal of Applied Polymer Science,2004,91(3):1746-1751.

[5]Babay A,Cheikhrouhou M,Vermeulen B.Selecting the optimal neural network architecture for predicting cotton yarn hairiness[J].Journal of the Textile Institute,2005,96(3):185-192.

[6]郝海涛，谢春萍.利用神经网络与AFIS纤维测试系统预测纱线质量[J].棉纺织技术,2003,31(8):477-480.

[7]Rumelhart D E,Hinton G E, Williams R J. Learning representations by back propagating errors[J].Nature,1986,323(11):533- 536.

[8]Storn R, Price K. Differential evolution ——a simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkeley: University of California, 1995.

[9]Ilonen J, Kamarainen J K. Differential evolution training algorithm for Feed-Forward neural networks[J].Neural Processing Letters, 2003(17):93-105.

[10]飞思科技产品研发中心.神经网络理论与MATLAB 7实现[M].北京:电子工业出版社, 2005:261.

[11]Storn R, Price K. Differential evolution ——a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[12]高岳林,刘军民.差分进化算法的参数研究[J].黑龙江大学自然科学学报,2009,26(1):81-85.