基于像素灰度关联的边缘检测

许悟生, 谢可夫

(湖南师范大学a.物理与信息科学学院，b.计算机教学部，中国 长沙 410081)

边缘检测是图像处理和计算机视觉中的基本问题，其目的是标识数字图像中亮度变化明显的点．边缘检测是底层视觉处理中最重要的环节之一, 也是图像分割、目标区域识别、区域形状提取等图像分析方法的基础，目前已经逐渐被广泛地应用于生物医学、模式识别以及工程技术中的零部件检查、故障诊断等更多领域．一直以来，如何准确快速地提取图像边缘是图像处理领域中的热点问题．

传统的边缘检测方法以微分算子法最为常用，其原理是通过对邻域内像素的灰度差分运算代替导数运算，然后根据导数或梯度考察图像小邻域灰度的跃变情况，构造边缘检测算子，如基于一阶微分的Roberts算子、Sobel算子、Prewitt算子、Canny算子和基于二阶微分的拉普拉斯(Laplacian)算子等[1]．因为各算子模板的构造特性,各算子对不同边缘的敏感程度不一，因此在检测边缘时，应根据不同类型的边缘采用合适的算子．但是，这些算子各有优缺点，Roberts算子和Laplacian算子对显著边缘变化的图像响应较好,抗噪能力较弱；而Sobel、Prewitt和Kirsch算子等具有较好的抗噪能力和图像响应，但其响应并未考虑中心像素灰度的影响；虽然Canny算子是目前传统检测算子中效果最好的一种，实验证明它的边缘强度估计和边缘定位优于其他算子,但它使用2×2的算子模板检测边缘梯度，使得它对边缘的准确定位有所偏差．

随着信息时代的不断发展，由于传统微分算子的局限性，有关边缘检测的新理论、新技术层出不穷，诸如边缘检测的小波变换算法，蚁群算法以及神经网络算法等[2-4]．20世纪后期，人类将量子力学理论引入到信息科学领域，量子信息科学[5]由此诞生，包括量子密码术、量子通信、量子计算机等几个方面，其理论和实验研究也随之取得了重大突破．20世纪80年代，Bennett和Brassard提出了著名的量子密钥分配协议——BB84协议[6]、Deutsch提出的量子图灵机概念[7]，充分证明了量子信息的高安全性和量子计算的强计算能力；20世纪90年代，Schumacher首次提出了量子比特的概念[8]，奠定了量子信息体系化的理论基础．随之，基于量子理论的图像处理新方法的研究得到了广泛的关注，如Chien-Cheng Tseng的量子图像处理方法[9]、邵桂芳等人提出的基于遗传量子的自适应图像分割算法[10]以及谢可夫所提出的量子衍生图像处理方法的研究[11]等，事实表明基于量子理论的图像处理方法的现实可行性和优越性．

本文提出将量子信息理论作为一种公理化数学体系，借鉴量子叠加态模型建立了邻域像素之间的相干性，并利用它们的相干性运算取代传统的模板卷积操作，实现了一种关联像素的量子衍生边缘检测算法．

1 量子系统的定义

量子比特(Qubit)是量子计算机中最基本的信息存储单位．一个量子比特是一个有两个基态的双态量子系统．与经典比特相比，量子比特的状态是基态|0〉和|1〉的线性组合，即

|φ〉=α|0〉+β|1〉，

(1)

其中α和β是复数，分别称为状态|0〉和|1〉的概率幅，它们满足

|α|2+|β|2=1，

(2)

(1)式表明，量子态|φ〉将以|α|2的概率得到态|0〉，以|β|2的的概率得到态|1〉．可以看出，量子比特的状态是二维复向量空间中的向量，其所有的运算都包容于希尔伯特(Hilbert)内积空间．

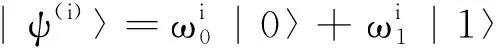
(3)

上式中，i2为i的二进制表示,态矢|i2〉则表示态|ψ〉的第i位基态，其概率幅为ωi，且满足归一化条件

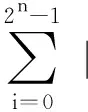
(4)

2 基于量子叠加的灰度关联

2.1 图像的量子比特表示

设一幅灰度级归一化处理后的数字图像f(m,n)，其中f(m,n)表示图像在像素点(m,n)处的灰度值，f(m,n)∈[0,1]，(m,n)∈Z2．基于对量子态的理解，假设f(m,n)表示像素点(m,n)∈Z2处灰度值为1的概率，1-f(m,n)为灰度值取0的概率，则图像f(m,n)可以用量子比特表示为：

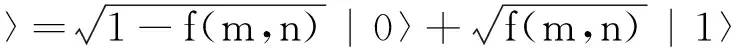
(5)

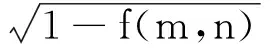
2.2 基于量子叠加的灰度关联

假设图像中(m,n-1)、(m,n)和(m,n+1)相邻3个像素点的灰度值分别为f(m,n-1)、f(m,n)和f(m,n+1)，简记为fm,n-1、fm,n和fm,n+1．根据量子态叠加原理，它们可以构成一个的小邻域灰度关联系统，其状态可表示为：

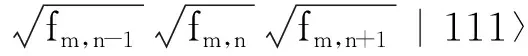
(6)

根据(3)式定义，上式中叠加态矢|i2〉前的系数分别为对应的概率幅ωi(m,n)．上述量子系统是一个8维Hilbert空间，其中任何一维态矢的概率|ωi(m,n)|2可构造一幅相应叠加态子图，能有效地对邻域像素间的灰度进行并行关联．

根据量子测量坍缩理论，若采用相应的测量算子组，仅对(6)式的第二量子位(对应中心像素点)进行测量，则其坍缩到0或1的概率均为0.5，且设坍缩到0、1后量子态分别为|Ψ0(m,n)〉和|Ψ1(m,n)〉，则有

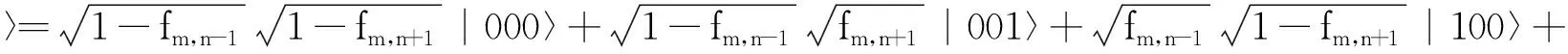
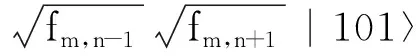
(7)

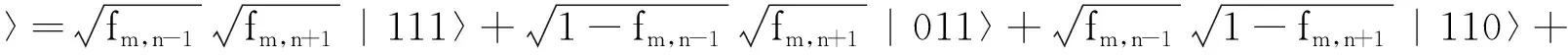
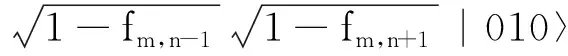
(8)

明显，上两式中得到态矢|011〉和|001〉的概率同为(1-fm,n-1)fm,n+1，|110〉和|100〉的概率同为fm,n-1(1-fm,n+1)．其中，态矢|011〉和|110〉的概率差为fm,n+1和fm,n-1的幅度差．由此，坍缩后的量子态运算可以构造Sobel算子模板．同理，Roberts算子模板可以通过对边上某点进行量子坍缩退化运算来实现．

3 图像边缘检测新方法

3.1 双向差分平均式

本文提出采用双向差分平均式描述邻域像素灰度的跃变情况，其实质是邻域内三像素的中心像素与其他两像素灰度的差分加权后的几何平均值，其具体构造过程如下：

在(6)式表示的图像量子关联系统中，态矢由三位二进制数组成，称从左至右出现01跳变的态矢为正走向态矢，如|011〉和|001〉，而出现10跳变的态矢称为负走向态矢，如|110〉和|100〉．此外在正、负走向态矢中，每个态矢有且仅有一对邻位构成跳变，若将构成跳变的两邻位取反则得到另一态矢，该态矢称为原态矢的反态矢，如态矢|011〉的反态矢为|101〉．

考虑到沿边缘梯度方向，邻域像素灰度的变化特征为逐渐增大或减小．在二进制数制中，正、负走向态矢的数值跳变情况正好对应了这一事实，其与相应反态矢的差式则反映了邻域(间隔为1的邻域)像素的跃变情况．

结合(6)式，利用所定义正、负走向态矢的概率与其对应反态矢的概率进行差运算，则有

(|ω011(m,n)|2-|ω101(m,n)|2)=(fm,n-fm,n-1)fm,n+1，

(|ω001(m,n)|2-|ω010(m,n)|2)=(1-fm,n-1)(fm,n+1-fm,n)，

(|ω100(m,n)|2-|ω010(m,n)|2)=(fm,n-1-fm,n)(1-fm,n+1)，

(|ω110(m,n)|2-|ω101(m,n)|2)=fm,n-1(fm,n-fm,n+1)，

可以看出，以上表达式均为相邻两像素灰度的差分与相应第三个像素点的灰度乘积，即对间隔为1的邻域差分结果进行了加权运算(自适应权数)，其权值大小取决于第三个像素点的灰度．这样邻域内三像素建立了一种新的相干方式．

针对以上概率差式，将两个相应的正、负走向态矢的差式的几何平均值称为双向差分平均式(以下简称平均式)，即：

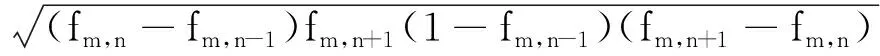
(9)

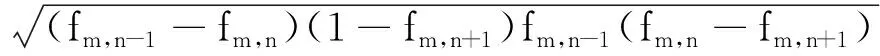
(10)

3.2 边缘检测算法

考虑到传统的Prewitt算子采用的3×3模板，但其定义的差分不能真实反映邻域三像素的灰度相互关联，提出利用平均式代替Prewitt算子差分，构建3×3的边缘检测模板．

以水平零角度方向为例，其双向差分平均式构造如下，先取得此方向上的正、负走向态矢与其对应反态矢的概率差式

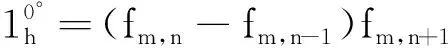
(11)

进而通过定义求得相应正、负走向的平均式

考虑水平45°和-45°方向的三量子位系统的平均式，可得

同理，对垂直各个角度方向进行分析，可得以下6个平均式

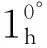
将上述6个水平平均式和6个垂直平均式，分别定义为水平和垂直边缘检测算子．提出取水平边缘检测算子中的正走向态矢平均式之和与负走向平均式之和的最大值，作为水平方向上的检测分量Gx；同理，取垂直边缘检测算子中正、负走向态矢平均式之和的最大值，作为垂直方向上的检测分量Gy，即

(12)

(13)

通过水平和垂直方向上的检测分量之和描述图像灰度跃变情况，即边缘灰度

G(m,n)=|Gx(m,n)|+|Gy(m,n)|.

(14)

3.3 边缘提取

本算法利用边缘灰度图像提取边缘的具体步骤描述如下：

(1)设定阈值．本算法选定边缘灰度的两倍均值作为提取边缘的阈值，即：th=2×mean(G(m,n))；

(2)对边缘灰度函数G(m,n)进行非最大值抑制法提取二值边缘图像函数fo．运算如下：

If

(G(m,n)>th)and(((Gx(m,n)≥(Gy(m,n)-ε))and(G(m,n-1)≤G(m,n))and(G(m,n)>G(m,n+1)))or

((Gy(m,n)≥Gx(m,n)-ε)and(G(m-1,n)≤G(m,n))and(G(m,n)〉G(m+1,n))))，fo(m,n)=1

else,fo(m,n)=0;

(3)输出边缘检测二值图像函数fo．

所提出算法利用3×3模板各个方向上的双向差分平均式来描述灰度跃变情况．相比Roberts算子，此方法增大了邻域关联范围，对噪声有一定的平滑作用；且其有效地将待检测的像素点作为模板的中心，准确地定位图像边缘．相比Priwitt算子和Sobel算子，此方法采用了间隔为1的邻域差分运算，且有效地兼顾相邻三个像素点的灰度影响，更能反映待检像素点处的灰度跃变情况．

4 仿真结果对比分析

本仿真实验是在Matlab环境下实现的．实验选取的两幅实验图片以及相应加噪(0.01椒盐噪声)图片，如图1(a)中前两幅图片为无噪原图，后两幅为相应的加噪图片；图1(b)、(c)、(d)分别为Sobel算法、Canny算法以及本文所提出算法对图1(a)中各图片进行边缘检测的仿真结果．其中，传统边缘检测的Sobel算法和Canny算法的检测结果由Matlab内的edge函数直接获得．

(a)原图 (b)Sobel算法

(c)Canny算法 (d)本文算法图1 仿真结果对比

由上图仿真结果可见，本文所提出的边缘检测算法对图像的灰度突变敏感，边缘定位精准，并且具有更好的抗噪能力．例如前两幅实验图片，可以明显看出所提算法提取的边缘细节丰富、轮廓清晰，定位准确；对比后两幅加噪图片，Sobel算法因噪声影响致使边缘丢失了部分细节，Canny算法则会在噪声点处产生通心粉效应，而本文所提算法检测出来的边缘不存在上述现象．综合而言，所提出算法提取边缘的效果较好，抗噪能力更强．

5 结束语

本文从量子理论出发，定义数字图像的量子比特表示形式，根据量子叠加理论衍生出邻域像素的并行关联形态，构造一种基于图像灰度处理的边缘检测算法．理论上，本算法兼顾地继承了Roberts算法对灰度变化的敏感性以及Priwitt算子和Sobel算法对噪声的平滑性能，边缘定位能力更强．通过与传统算法仿真结果对比分析，验证了该算法的有效性和优越性．

参考文献：

[1] 张德丰.MATLAB数字图像处理[M].北京：机械工业出版，2009.

[2] MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J].IEEE Trans on Inf Theor, 1992,38(2):617-643.

[3] 张 健,何 坤,郑秀清，等.基于蚁群优化的图像边缘检测算法[J].计算机工程, 2011,37(17):191-193.

[4] 车国锋,刘忠领,李军伟,等.神经网络边缘拟合[J].红外与激光工程, 2003,32(4):422-426.

[5] 赵生妹，郑宝玉.量子信息处理技术[M].北京：北京邮电大学出版社，2010.

[6] BENNETT C H, BRASSARD G. Quantum cryptography:public key distribution and coin tossing[C]//Proc IEEE Ⅱ Conf Computers, Systems and Signal Processing.India, Bangalore, 1984.

[7] DEUTSCH D. Quantum theroy, the Church-Turing principle and the universal quantum computer[J].Proc Roy Soc London A, 1985,400(1818):97-117.

[8] SCHUMACHER B. Quantum coding[J].Phys Rev A, 1995,51(4):2738-2747.

[9] TSENG C C, HWANG T M. Quantum digital image processing algorithms[C]//16th IPPR conference on computer vision,graphics and image processing, Kinmen, Taiwan, 2003.

[10] 邵桂芳,李祖枢,刘 恒,等.基于遗传量子的自适应图像分割算法[J].计算机工程, 2005,31(22):189-191.

[11] 谢可夫.量子衍生图像处理方法的研究[D].长沙：中南大学,2007.