非局部混合噪音滤波器MNF的一种快速算法

罗晓军

(1．商丘职业技术学院计算机系，中国 商丘 476000；2．长沙理工大学数学与计算科学学院，中国 长沙 410076；3．商丘广播电视台，中国 商丘 476000)

数字图像在获取、传输和存贮过程中常常会受到各种噪音的干扰，最常见的是高斯噪音和脉冲噪音的混合干扰．近年来，许多学者一直致力于这类混合噪音的滤波算法研究，提出了诸多优秀算法[1-13]．其中，文献[1] 是在Bilateral滤波器(仅适于去除高斯噪音)的基础上，把脉冲噪音统计量ROAD(Rank ordered absolute difference)引入其中，构建了Trilateral滤波器，使其同时具有去除高斯噪音和脉冲噪音的能力，这是当时去除混合噪音最好的算法；2010年李兵等人在提出相似假设，证明相似原理之后，提出了一种混合噪音非局部滤波算法[9](Mixed noise filter,简称MNF)，此算法的关键思想之一是构造了一个新的加权“脉冲过滤范数”，使得MNF去除混合噪音的效果明显优于Trilateral滤波算法及其他已有方法；2011年袁莉芬等人通过先分析混合信号特征，建立基于独立成分分析技术的信号模型，然后最大化信号独立性特征，分离有用信号与噪音信号，实现了去噪目的[10]；2012年2月，Hu等人提出了非局部混合滤波器(NLMixF)[11]，该滤波器不仅提高了Trilateral滤波器的性能，而且扩展了非局部均值滤波器，等等．上述这些算法有些属于局部算法[1，10]，有些属于非局部算法[9，11]，但是从滤波效果上看，当噪音图像所含高斯噪音较多时，非局部滤波算法的效果常常更好些．

在MNF算法中，由于采用了非局部思想，所以它与非局部均值一样存在着较大的计算负担．例如，一个512×512的图像，如果邻近窗口取9×9，邻域窗口取5×5，滤波时需要运行时间为130 s左右(硬件为：CPU AMD2500+，内存512 MB．软件为：Windows XP.net2.0 C#2.0)，况且，在实际操作中，为了得到更好的去噪效果，有时还要增大邻近窗口或邻域窗口，这必然又增大了算法的计算量，降低了运行效率．

对于非局部算法中存在的较大计算负担问题，人们一直在寻找某种快速算法，并取得了一定的成果[12-13]．2005年，由美国明尼苏达大学的Mona Mahmoudi等人提出了“邻域像素分类法”[12]，根据两像素的均值和梯度的相似程度判定是否参加滤波计算，对非局部均值(NL-Mean)算法进行了改进，使NL-Mean的计算负担问题得到明显改善，其运算速度比原来提高了近30%．

但是，像素的梯度是容易受噪音类型和噪音级别影响的量，噪音的类型不同或级别不同，像素的梯度也有很大差别，所以仅使用梯度和均值作为判断条件就有可能对邻域窗口的相似程度判断不准确．为此，本文提出一种新的邻近像素分类法，该方法使用邻近窗口像素的均值比、梯度比和方差比作为判断条件，认为均值比、梯度比和方差比均在给定的阈值范围内的像素才是真正相似的像素,仅让这部分像素参加滤波计算，其余像素被忽略不计．大量的实验结果表明，这种预分类方法运用于MNF算法中，不仅提高了滤波效果，而且运算速度比原来提高了20%以上．

1 算法描述

本文约定：u(i)表示数字图像u在点i处像素的灰度值(0≤u(i)≤255)，i∈I={0,1,…,M-1}×{0,1,…,N-1}，v表示噪音图像．

高斯噪音模型为：v(i)=u(i)+n(i)，其中n(i)为相互独立的、均值为0的、标准差为σ的高斯变量．

脉冲噪音模型为：v(i)以概率p取值n(i)，以概率1-p取值u(i)，p是脉冲噪音发生概率，n(i)是相互独立的取值于{0,1,…,255}中的随机变量．

图1 邻近窗口V(i)和邻域窗口Ni和Nj

1.1 MNF算法描述

(1)

其中

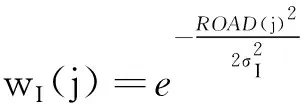
(2)

对窗口Ni和Nj=T(Ni)，向量v(Ni)-v(Nj)的脉冲过滤范数记为‖v(Ni)-v(Nj)‖M，其值为：

(3)

其中

(4)

σM,σI,σJ为滤波参数．为简便起见，实验中取σI=σJ．

该算法存在着较大计算量，其原因在于(3)式的范数计算，如图1所示，图中Vi是以i为中心的邻近窗口，Ni和Nj分别是以i和j为中心的邻域窗口．对某像素点i来说，Vi中所有的像素点j都要进行(3)式脉冲过滤范数的计算．而且，窗口Vi越大，计算量越大，窗口Ni、Nj越大，计算量也越大．

1.2 非局部均值(NL-Mean)的快速算法

2005年，由Mona Mahmoudi等人提出的像素分类法[12]是对邻近窗口内的像素分类，减少邻近窗口中参加范数计算的像素数量，从而提高非局部均值滤波算法的速度．其主要算法为：

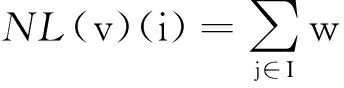
(5)

(6)

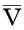
此算法利用(6)式把Vi窗口内像素分成两类，即:在Vi窗口内梯度和均值与中心像素相似的像素为一类，这类像素参加(6)式的范数计算；其余为另一类，不参加(6)式的范数计算，这就可能减少范数计算的次数，节约了运算时间，提高了运算速度．

1.3 Fast-MNF算法描述

在MNF的算法中，(3)式也同样遇到类似的范数计算，这也是造成MNF算法运算速度慢的原因，为了提高MNF算法的运算速度，我们把Mona Mahmoudi等人提出的快速算法的思想引入到MNF算法．由于加性高斯噪音零均值的特性和脉冲噪音的高频、孤立、大偏差的特点，用像素邻近区域的灰度平均值作为判断像素相似性的依据是合理的，而梯度又能够很好地反映像素邻近区域结构信息的相关性，同时，邻近区域像素灰度值的方差也是一个能很好地反映像素之间相关性的量．因此，本文结合均值、梯度和方差，提出一种新的快速算法(称之为Fast-MNF)，用Fast-MNF恢复后的图像表示为(7)式．

(7)

其中

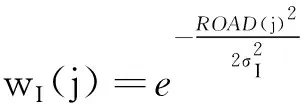
(8)

(9)

由(9)式可知，当Ni和Nj的均值比、梯度比和方差比均在给定的阈值范围内时，说明i和j是相似像素，wM(i,j)取值较大，像素j的贡献就越大．这样的j参加(9)式的范数运算，否则，不参加运算．

2 仿真实验的参数选取

实验时，我们选取多个标准灰度图像进行对比实验，图像大小为：512×512，灰度级为256．算法中各参数的取值是：

(1)D=4,d=2,即邻近窗口为9×9,邻域窗口为5×5；σ1∈(0.9,1)，σ2∈(1,1.1)，η1∈(0.4,0.6)，η2∈(1.2,1.5)，ω1∈(0.2,0.4)，ω2∈(1.6,1.9)．

3 实验结果

表1和表2是Fast-MNF和MNF 2种算法去噪图的峰值信噪比(PSNR)和运行时间的比较．

表1 Fast-MNF和MNF处理纯高斯、纯脉冲噪音时PSNR、运行时间比较(以Lena为例)

表2 Fast-MNF和MNF处理混合噪音时PSNR、运行时间比较(以Lena为例)

表1、表2列出了对Lean图像去噪的部分结果，由表可见， Fast-MNF的去噪效果(PSNR)比MNF稍好些，而在运行速度上，Fast-MNF比MNF却有较大提高．对于纯高斯噪音而言，噪音级别越高，提高的速度越大，如表1中，对σ=10的噪音，速度提高了25.17%，对σ=40的噪音，速度提高了25.93%；对于纯脉冲噪音和混合噪音而言，噪音级别越低，提高的速度越大，如表1中，对p=10%的噪音，速度提高了40.80%，而p=40%，速度只提高了23.91%；但是，当高斯噪音中混有脉冲噪音时，其滤波速度却随高斯噪音级别的升高而减慢，如表2中，对σ=10p=20%的噪音，速度提高了24.44%，而σ=40p=20%，速度提高了21.70%．

总之，通过大量的实验证明，Fast-MNF算法对各种噪音类型滤波效果均有不同程度的提高，且运算速度可提高20%以上．

4 结论

针对MNF滤波器存在着较大的计算负担问题，本文提出一种基于均值、梯度和方差相似性的混合噪音滤波器快速算法(Fast-MNF)，该算法的滤波过程分2个阶段进行，第一阶段是对邻近窗口像素进行预分类，它把邻近窗口像素按其均值、梯度和方差的相似程度分成2类，相似的像素为一类，参与第二阶段的滤波计算，不相似的像素被忽略；以此来提高滤波速度．大量的仿真实验结果表明，Fast-MNF算法对各种噪音类型，其滤波效果均优于MNF，滤波速度提高20%以上．因而，Fast-MNF算法比MNF更具有实用性．

参考文献：

[1] GARNETT R, HUEGERICH T, CHUI C,etal. A universal noise removal algorithm with an impulse detector[J]. IEEE Trans Image Process, 2005,14(11):1747-1754.

[2] DABOV K, FOI A, KATKOVNIK V,etal. Image denoising by sparse 3D transform-domain collaborative filtering[J]. IEEE Trans Image Process, 2007,16(8):2080-2095.

[3] KATKOVNIK V, FOI A, EGIAZARIAN K,etal. From local kernel to nonlocal multiple-model image denoising[J]. Int J Comput Vis, 2010,86(1):1-32.

[4] 周 刚,贾振红,覃锡忠.一种新的图像去噪混合滤波方法[J].激光杂志, 2007,28(1):57-59.

[5] 王建勇,周晓光,廖启征.一种基于中值-模糊技术的混合噪声滤波器[J].电子与信息学报, 2006,28(5):901-904.

[6] 罗晓军,李 兵,刘全升，等.一种新的线性混合滤波器[J].计算机工程与应用, 2008,44(17):172-174.

[7] 张秀荣,孟和达来.数字图像处理系统的开发与研究[J]. 湖南师范大学自然科学学报, 2011,34(6):35-39.

[8] 罗晓军,王世秀,李 兵,等. 基于ROLD的混合噪音线性滤波器[J]. 计算机工程与应用, 2010,46(31):175-177.

[9] 李 兵,刘全升,徐家伟,等.去除混合噪音的一种新方法[J].中国科学信息科学, 2010,40(9)：1165-1175.

[10] 袁莉芬,刘 辉,程 俊.基于独立成分分析技术的语音除噪系统[J]. 湖南师范大学自然科学学报, 2011,34(3):24-26.

[11] HU H J, LI B, LIU Q S. Non-local filter for removing a mixture of Gaussian and impulse noises[C]//VISAPP 2012. Rome:Sci Te Press, 2012.

[12] MAHMOUDI M,SAPIRO G. Fast image and video denoising via nonlocal means of similar neighborhoods[J]. IEEE Signal Proc Let, 2005,12(12):839-842.