非圆齿轮齿条机构的设计

郑方焱，吴梦杰

(湖北汽车工业学院 机械工程系，湖北 十堰 442002)

非圆齿轮具有体积小、结构紧凑、刚性好、传动扭矩大等优点,已被广泛应用于机械设备的各个领域，但只能传递变速比的回转运动，不能改变运动形式；将圆柱齿轮齿条传动扩展应用于变速比传动领域可得到非圆齿轮齿条机构，该机构可直接将回转运动转化为特定工作要求的直线运动。本文阐述了其设计原理、啮合方程，并以实例验证了设计的正确性。

1 齿条节曲线的设计

图1所示为非圆齿轮和齿条的运动位置关系，若已经非圆齿轮的节曲线极坐标方程为

式中：φ1为主动轮1的转角。则直角坐标方程为

由于中心距保证不变，对于齿条的节曲线

由图1可知，当非圆齿轮转1周时，齿条直线移动距离为s,若非圆齿轮2节曲线封闭，则设任一时刻齿条曲线的水平位移为x2，由微分几何可得到此时非圆齿轮转过的弧长：

而齿条移动过的弧长为

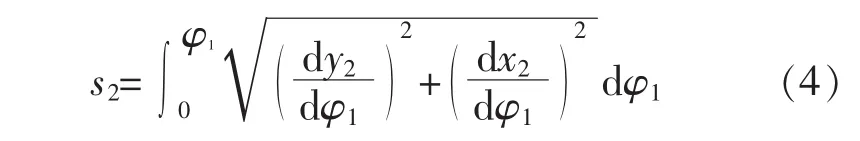
由节曲线滚动理论可知

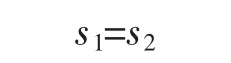
联立式（3）～（4）化简可得节曲线横坐标的计算公式

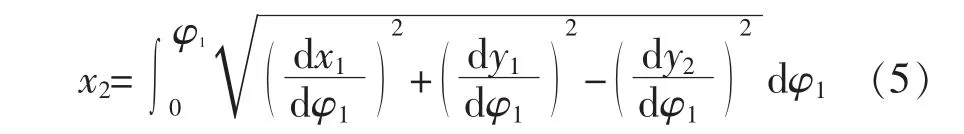
在齿轮传动中，传动比是一个非常重要的概念，如上所述，传动比在任意时刻发生着变化，故可表示为

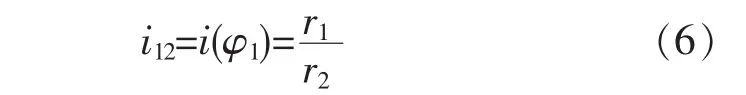
或

这里推出的传动比不再是两轮角速度之比，而是由于运动形式发生了改变，成了一种广义上的传动比。同样的，可利用传动比函数来设计机构，以满足特定运动要求。

3 齿廓求解

3.1 齿轮齿廓方程的求解

图2显示的共扼齿条的数学形状，设其每段坐标向量为

图2中有5段直线，4段圆弧。齿廓的形状参数可将rr,i表达出来。

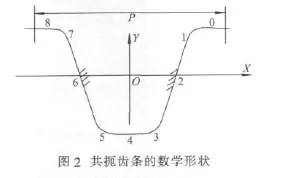
齿轮的齿廓曲线是共扼齿条模型和节曲线纯滚动模型按齿轮啮合原理引结合而成［2］。在本问题中，由啮合原理可直接得到

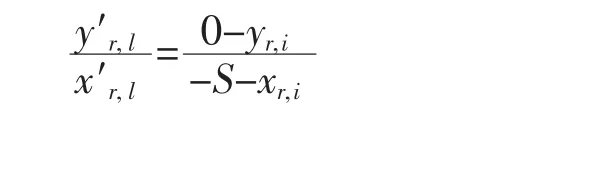
设齿廓坐标由向量

给出，则坐标变换关系为

变换矩阵

联立上述方程即得到齿廓的方程，其第2段方程如下：

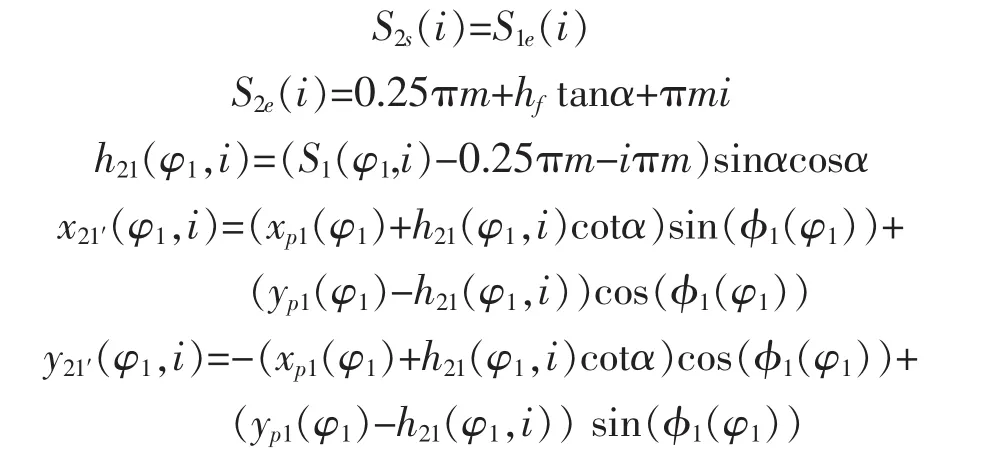
3.2 齿条齿廓方程的求解

如图3所示，在非圆齿轮回转中心上建立定坐标系OXY，在非圆齿轮上建立随动坐标系O1X1Y1，在齿条上建立随动坐标系O2X2Y2。

图3中φ1为非圆齿轮的极角，s为齿条的极位，即由式 （4）得到从坐标系O1X1Y1到坐标系O2X2Y2的变换矩阵：

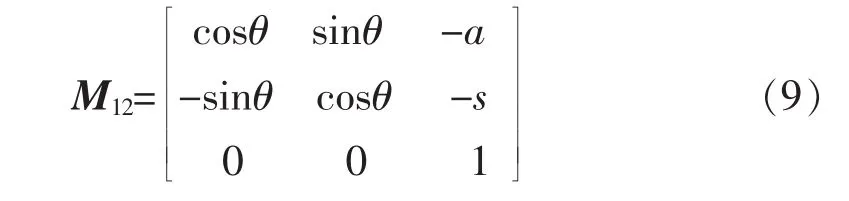
对前述非圆齿轮齿廓方程进行坐标变换，得到齿条的齿廓坐标：

4 实例计算与分析

给出传动比函数为

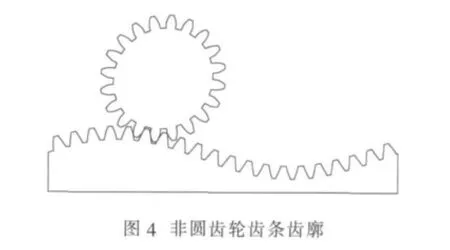
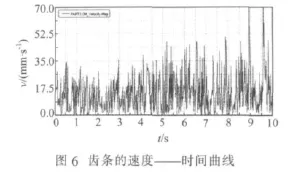
中心距为50，z为20，m为2.75。基于上述思想，得到一对非圆齿轮齿条传动其图形学仿真结果如图4所示。最后运用PROE进行实体建模，导入ADAMS中装配和设置约束，如图5所示。最后进行动力学分析，得到齿条的速度时间曲线如图6所示。

5 结语

图形学仿真结果和运动学仿真的结果验证了该设计思路和方法的正确性。

运用上述机构能通过简单的一级传动即所获得特定运动规律的直线运动，机构紧凑，传动效率高，应用前景十分广泛。

齿条和非圆齿轮一样能在通用的数控插床上加工，有利于产品化，规模化。

［1］ 潭伟明,梁燕飞，安军，陈就.渐开线非圆齿轮的齿廓曲线数学模型［J］.机械工程学报，2002,38（5）：75－79.

［2］ 吴序堂.齿轮啮合原理［M］.西安：西安交通大学出版社，2009.

［3］ 郑方焱，任爱华，孙传琼，等.非圆齿轮条机构：中国，2011201012243［P］.2011－11－23.