密闭爆发器试验过程壁温变化研究

张薇薇，狄加伟，张明安，屈 洁

(西北机电工程研究所，陕西 咸阳 712099)

随着科学技术的迅猛发展，高性能发动机系统、超高速高射频武器系统等各种高性能设备的研制成为工业与国防发展的必然，密闭腔内工作过程的高参特性(高温可达2 500～2 800 K、高压可达300～ 500 MPa、高瞬态性约为5～10 ms)将更加明显，毫秒级传热过程对零部件形成了更高的热负荷与机械负荷，进而产生的烧蚀、热应力、变形、热物性变化等对设备的机械性能、使用性能与寿命、安全性及产品的生产过程与质量监控等都带来了很大的挑战，已成为研究者们关注的热点。经过多年的工作，人们已经认识到，同样的材料，烧蚀与密闭腔内壁承受的峰值温度密切相关，甚至可以认为是最重要的参量，而且其他许多特性也与密闭腔壁内外温度分布直接相关[1]。

笔者针对密闭爆发器建立内弹道模型及单层圆筒壁轴对称传热模型。在该模型的基础上，通过选择合理的计算方法编制了程序。利用该程序对密闭爆发器试验的燃烧过程及筒壁传热过程进行了分析计算，研究了容器壁温的变化规律。

1 物理模型

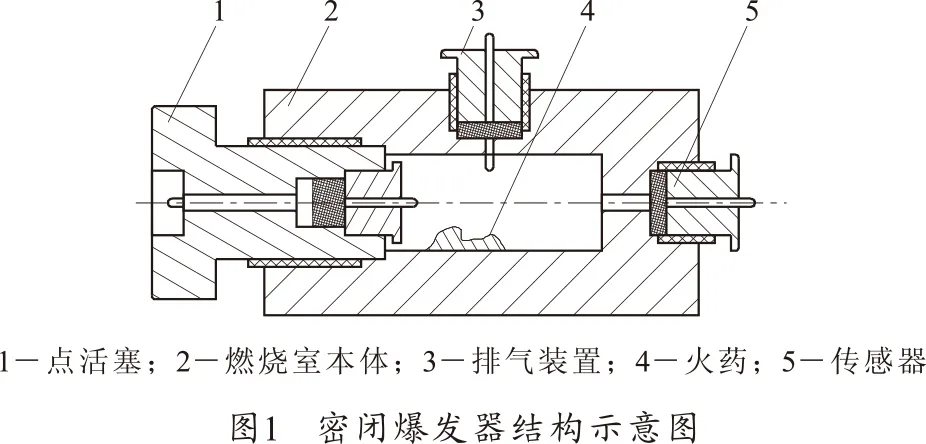
图1为密闭爆发器的结构示意图。密闭爆发器的本体是用炮钢制成的圆筒，在其两端开口的内表面制有螺纹。一端旋入点活塞，依靠电流点燃点火药，从而使火药着火燃烧。产生的压力及其随时间的变化规律，则由另一端旋入的测压传感器并通过记录仪器记录。

1.1 基本假设

1.1.1 火药燃烧基本假设

当不计密闭爆发器的变形时，整个火药燃烧过程为定容状态，火药气体没有做功和宏观流动，火药燃烧结束时，容器内的压力达到最大值[2-5]。火药燃烧基本假设条件为：

1)火药燃烧服从几何燃烧定律和指数燃速定律。

2)燃气组分始终保持不变。

3)火药燃烧过程中，密闭爆发器容积不变。

1.1.2 传热过程基本假设

1)忽略火药气体气对固壁的摩擦及其热效应，火药气体与密闭容器内表面只有辐射换热。

2)忽略固壁内热量的轴向传递。

3)温度场具有轴向的对称性。

4)不考虑火药燃烧期间的热量传递，计算起始点为火药燃烧结束的时刻。

5)火药点火燃烧后生成火药气体温度视为火药爆温。

6)火药气体在密闭容器内均匀分布，没有气体流动，气体的流动速率为0。

7)密闭容器内外壁材料均相，导热系数为常量。

8)环境温度为18℃，空间足够大。

1.2 密闭爆发器火药燃烧实验模型

1)火药燃速方程

(1)

式中:z为火药已燃相对厚度;e1为火药弧厚;u1为火药燃速系数;n为燃速指数;p为平均压力。

2)火药形状函数

(2)

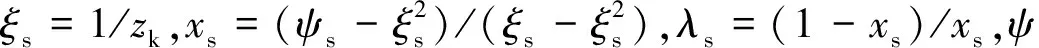
3)火药气体定容状态方程

(3)

式中，f为火药力;ω为装药质量;W0为点火药室体积;ρp为火药密度;α为火药气体余容。

将方程(1)～(3)化为微分方程组:

(4)

其中，ψ、z、p为未知量，有4个方程，对t按一定步长取值，用龙格-库塔法解方程组。

1.3 传热模型

热传导方程

(5)

式中:T为容器固壁的温度;t为时间;r为容器固壁中某点距身管对称轴的距离;a为容器固壁的导温系数。

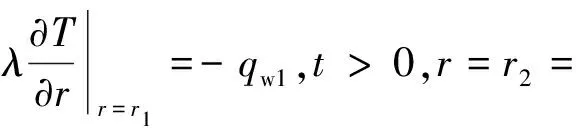
对方程(5)采用对于时间的偏导数取向前差分，对r的偏导数取中心差分，得到：

(6)

容器内壁面边界差分形式为：

(7)

容器外壁面边界差分形式为：

(8)

2 数值计算结果及分析

火药及装药参数见表1。

表1 火药及装药参数

表1中给出了试验数据，利用密闭爆发器模型计算的压力随时间变化的曲线如图2所示。可以看出，整个密闭爆发器试验过程不到8 ms，密闭容器内的压力上升到最大值620 MPa左右，当容器内压力达到最大时，火药燃烧结束。

容积为100 ml的密闭爆发器火药燃烧的压力模拟结果如图2所示，可以看出计算结果与实验结果的误差较小。

火药气体与容器内壁面辐射换热量较小，所需要的时间较长。计算时选取了4个时间点，分别为30 s、1 min、3 min和5 min。其模拟计算结果如图3～图8所示。图3为火药气体温度曲线；图4～图7为温度随时间及壁面厚度(径向)变化的二维曲线；图8为容器内壁面及外壁面的温度变化曲线。

从图3中可以看出，当火药开始燃烧时，密闭容器内的火药气体温度瞬间从环境温度陡升到火药的爆温，随着火药燃烧结束，火药气体温度呈逐渐下降趋势，直到2 600 K左右。

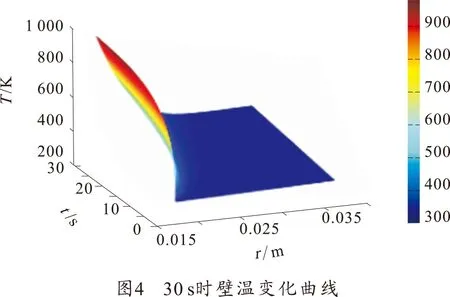
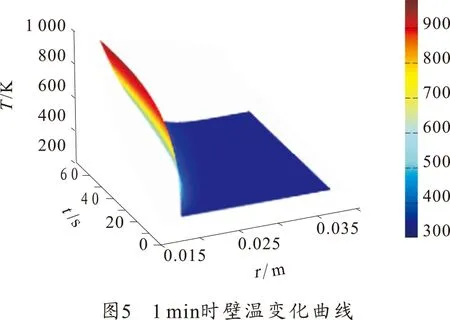
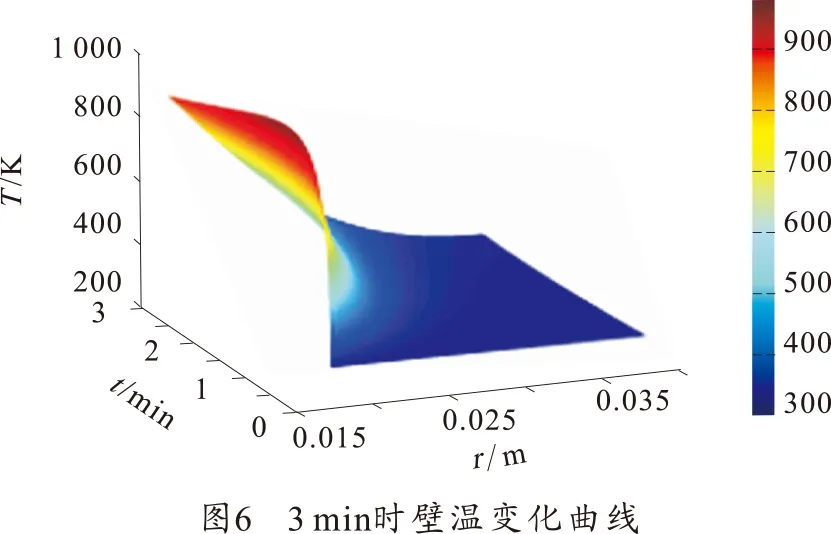
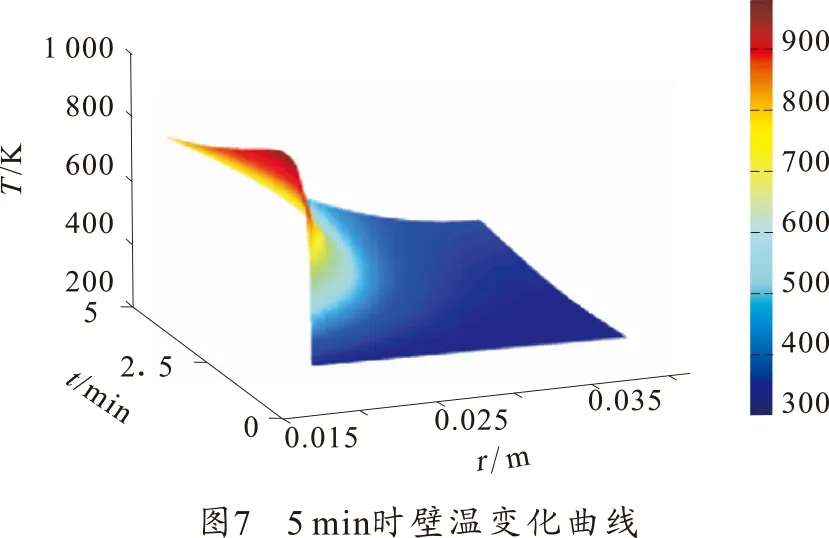
如图4～图7所示，随着时间的变化，密闭爆发器内壁面的温度从970 K下降至760 K左右，外壁面温度由环境温度上升到380 K左右。

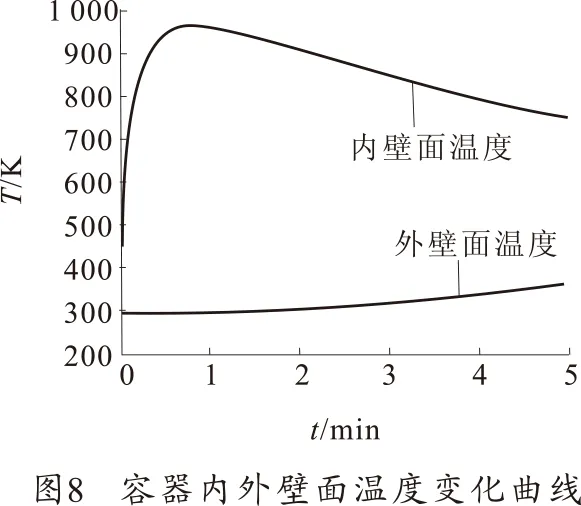
图8为容器内壁面及外壁面的温度变化曲线。从图中可以看出，在火药燃烧时及冷却期内容器内壁面上升梯度较大，主要是因为此期间的气体温度和壁面温度之间的温差最大，而温差与换热量成正比关系。与容器内壁面相比外壁面温度上升较为缓和，如图4～图7所示，在1 min时，外壁温度还保持在环境温度，在3 min时外壁温度才开始上升，并且可见升温猛烈部分主要在容器内壁面1 mm左右的薄层内。

3 结 论

本文针对密闭爆发器建立了内弹道模型及单层圆筒壁轴对称传热模型，对密闭爆发器试验过程进行了分析计算，求出了密闭爆发器内的压力曲线并与试验结果进行了对比，计算得到了火药气体温度的曲线、容器内壁面及外壁面的温度变化曲线。数学模型及仿真程序，对分析密闭爆发器试验传热过程及火炮射击热安全性提供参考。

参考文献(References)

[1] 黄凤良，余永刚.密闭腔内快速传热中壁面温度的软测量方法[J].传感技术学报，2003(3):355-358.

HUANG Feng-liang, YU Yong-gang. The soft-sensing method on in-wall temperature during flash heat transfer flash heat in closed-chamber[J]. Journal of Sensors and Actuators，2003(3):355-358.(in Chinese)

[2] 王普法，官汉章.密闭爆发器压力损失及其修正方法[J].弹道学报，1992(2)：15-20.

WANG Pu-fa,GUAN Han-zhang. The correcting method for pressure loss in closed bomb[J]. Journal of Ballistics, 1992, (1): 15-20.(in Chinese)

[3] 黄凤良，夏春梅，周彦煌，等.温度测试的外推方法[J].计量学报，2003，24(2)：116-119.

HUANG Feng-liang, XIA Chun-mei, ZHOU Yan-huang，et al. Extrapolation method for the measurement of temperature[J]. ACTA Metrologica Sinica，2003，24(2)：116-119.(in Chinese)

[4] 芮筱亭，贠来峰，王国平，等.弹药发射安全性导论[M].北京:国防工业出版社，2009.

RUI Xiao-ting, YUN Lai-feng, WANG Guo-ping，et al.Direction to launch safety of ammunition[M]. Beijing:National Defense Industry Press,2009.(in Chinese)

[5] 赵军，廖昕，王泽山.密闭爆发器试验过程中的热散失修正研究[J].含能材料，2009，17(2)：725-730.

ZHAO Jun, LIAO Xin, WANG Ze-shan. Heat loss correction in closed bomb tests[J]. Journal of Energetic material，2009，17(2)：725-730.(in Chinese)

[6] 周彦煌，王升晨.实用两相流内弹道学[M].北京：兵器工业出版社，1990:278-283.

ZHOU Yan-huang, WANG Sheng-chen. Practical interior ballistics of two-phase flow[M]. Beijing:The Publishing of Ordnance Industry,1990:278-283.(in Chinese)

[7] 郁圣杰.火炮发射过程中的身管热分析及其应用[D].南京:南京理工大学，2004

YU Shen-jie. Study and application of the heat transfer on tube of gun during launching[D].Nanjing:Nanjing University of Seienee&Technology，2004.(in Chinese)

[8] 杨世铭.传热学[M].2版.北京：高等教育出版社，1992:213-218.

YANG Shi-ming. Heat transfer[M].2nd ed. Beijing: Higher Education Press, 1992:213-218.(in Chinese)