防空多管火箭武器跟踪发射模型研究

任 杰，马大为，朱忠领，朱孙科

(南京理工大学 机械工程学院, 江苏 南京 210094)

1 参考坐标系及坐标系之间的转换

防空火箭炮作跟踪运动时，发射装置在时刻运动，研究时需要建立发射装置与火箭弹的相关坐标系，完成各坐标系之间的转换。选取合适的参考坐标系来研究火箭弹的运动规律，会使方程形式简单、便于求解[1]。本文选取的几种参考坐标系[1-4]如图1所示，方向均按右手定则确定。

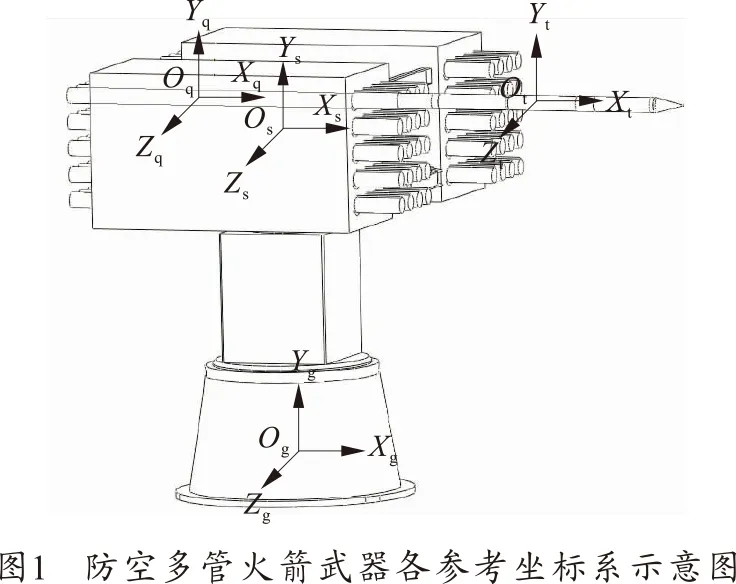
1.1 相关参考坐标系

1.1.1 地面坐标系Og-XgYgZg

地面坐标系与地球表面固连，选取发射装置方位回转中心在水平面的投影为坐标原点Og，OgXg轴平行于定向器轴线在水平面的投影，向前为正。OgYg轴垂直于水平面，向上为正。OgZg轴垂直于OgXgYg平面。

1.1.2 随动坐标系Os-XsYsZs

坐标系原点Os取在随动装置的俯仰回转轴与方位回转轴中心线的交点处，OsXs轴平行于定向器轴线在水平面的投影，向前为正。OsYs轴沿随动装置的方位回转轴中心线，向上为正。OsZs轴沿随动装置的俯仰回转轴。

1.1.3 定向器坐标系Oq-XqYqZq

坐标系原点Oq取为定向器中心线与OsYsZs平面的交点处，OqXq轴沿射向，OqYq轴在定向器纵向对称面内，向上为正，OqZq轴垂直于发射架纵对称面OqXqYq。

1.1.4 弹体坐标系Ot-XtYtZt

坐标系原点Ot取在火箭弹质心处，OtXt轴与火箭弹几何纵轴重合，指向弹头为正，OtYt轴在弹体纵向对称平面内，向上为正，OtZt轴垂直于OtXtYt平面。

1.1.5 弹道坐标系Od-XdYdZd

坐标系原点取在火箭弹质心处，OdXd轴与火箭弹速度方向重合，OdYd轴在弹体纵向对称平面内，向上为正，Zd轴垂直于OdXdYd平面。

1.2 参考坐标系之间的转换关系

描述弹体运动的各种参量，可以通过各坐标系及其坐标系之间的相互关系来考察。将坐标系写为矩阵形式，设坐标系之间的转换矩阵为T，采用上下标的方式区分源坐标系和目标坐标系，下标代表源坐标系，上标代表目的坐标系[6]。本文限于篇幅，在此不展开各坐标系之间转换矩阵，请参考有关文献[1]。

随动坐标系与地面坐标系之间的转换:

(1)

定向器坐标系与随动坐标系之间的转换:

(2)

定向器坐标系与地面坐标系之间的转换，由式(1)和式(2)可得：

(3)

(4)

弹道坐标系与地面坐标系之间的转换:

(5)

弹道坐标系与发射装置坐标系之间的转换，采用地面坐标系进行过渡转换，由式(1)和式(5)可得：

(6)

(7)

弹体坐标系与地面坐标之间的转换：

(8)

弹体坐标系与定向器坐标系转换，发射前弹体坐标系各坐标轴与定向器坐标系各坐标轴平行。

(9)

2 多管火箭发射装置的运动方程

防空多管火箭发射装置在随动系统的控制下对空中目标(低空飞行的巡航导弹或制导炸弹)进行跟踪，需要将发射方向或火箭弹速度的方向指向目标或目标前置点，发射装置的运动特性与目标的运动规律密切相关。发射装置在空间中的运动是由绕俯仰轴的转动和绕方位轴的转动所合成的，研究时将发射装置的运动分解为绕俯仰轴和绕方位轴的转动。这两种运动对火箭弹离轨运动参数产生的影响都不能忽略，不论发射装置调转的角速率多大，其对火箭弹离轨的影响都必须考虑。如不考虑发射装置调转角速度的影响，将会使计算得到的火箭弹的离轨参数不准确，使得空间弹道解算存在误差，当攻击空中目标时，较小的误差也会使火箭弹偏离目标。

研究时假设多管火箭武器发射装置为刚体，则可以将发射装置绕俯仰和方位回转轴的回转运动简化为刚体绕定轴转动问题。

(10)

式中：φf为俯仰转角;ωf为瞬时俯仰角速度;εf为瞬时俯仰角加速度。

发射装置绕方位回转轴转动的一般运动方程为:

(11)

式中：φh为方位转角;ωh为瞬时方位角速度;εh为瞬时方位角加速度。

式(10)与式(11)为发射装置绕轴转动的一般运动方程，依据公式可确定火箭弹在离轨瞬间发射装置的瞬时绕轴转动角速度，发射装置的绕轴转动角速度是计算火箭弹牵连速度所需参数之一。

3 跟踪发射时火箭弹离轨参数的确定

防空多管火箭炮对空中目标进行跟踪发射时，火箭弹的速度、攻角和偏角等运动参数均随发射装置的运动而进行变化，发射装置的运动特性对火箭弹的运动产生了很大的影响。空间弹道的解算需要火箭弹离轨参数作为初始条件，而离轨参数又受到发射装置运动的影响，在计算火箭弹离轨参数时，需要将发射装置的运动与火箭弹的运动相耦合，才能获得准确的离轨参数表达式，从而保证对目标的命中精度，提高火箭弹的毁伤率。为便于研究，假设火箭弹为刚体，不考虑弹体变形，不计推进剂的损耗，认为质量不变，转动惯量恒定，只受推力、重力与科氏惯性力的作用，弹体的运动可以视为质心的移动和绕质心的合成运动[3,7]。

3.1 火箭弹绝对离轨速度

跟踪状态下发射装置在随动系统的控制下绕俯仰轴和方位轴转动，发射装置的绕轴转动给火箭弹的运动带来牵连速度，如果将发射装置的运动速度分解为绕俯仰轴的转动速度和绕方位轴的转动速度，则火箭弹的绝对离轨速度在地面坐标系中可表示为[3,5]

V=Vr+ωf×rf+ωh×rh

(12)

式中：V为火箭弹绝对离轨速度;Vr为火箭弹相对定向器的离轨速度;ωf×rf和ωh×rh分别为离轨时刻发射装置绕俯仰回转轴和方位回装轴转动产生的牵连速度;ωf和ωh为离轨时刻发射装置绕俯仰回转轴和绕方位回转轴的转动角速度;rf和rh为离轨时刻火箭弹质心到发射装置俯仰回转轴和方位回转轴的矢径。

相对离轨速度Vr沿定向器坐标系的OqXq方向，将Vr投影至地面坐标系，其各向分量为:

通过对智能工程建设过程中各阶段的了解，发现智能工程建造中存在着各种影响因素。因此，为确保政府大楼智能工程项目可以按时保质完成，需要在智能工程建设施工中进行方案设计，做好工程进度控制。

(13)

将ωf、rf、ωh、rh分别转换到地面坐标系中，并写为矩阵形式。

(14)

(15)

(16)

(17)

(18)

(19)

将式(13)、式(18)、式(19)代入式(12)中，可求解得火箭弹绝对离轨速度V。

V=Vr+ωf×rf+ωh×rh

(20)

由式(20)可知，火箭弹的绝对离轨速度与火箭弹的相对离轨速度、发射装置的俯仰回转角速度、方位回转角速度、火箭弹质心至俯仰回转轴与方位回转轴的矢径有关。多管火箭炮装弹数量较多，每一枚火箭弹的位置都不相同，在离轨瞬间，火箭弹的质心至俯仰回转轴与方位回转轴的矢径均不相同，发射装置的运动将导致每一枚火箭弹都具有不同的离轨运动参数，其对应的空间弹道也都不相同。发射时，火控计算机需要根据离轨参数表达式针对每一枚火箭弹设定相应的参数计算其对应的离轨参数，从而保证其空间弹道初始条件的准确，使火箭弹能够命中或毁伤目标。

对于既定结构的防空多管火箭炮来说，每根定向器中火箭弹离轨时质心至回转轴的距离是固定的，火箭弹离轨时发射装置绕俯仰轴和回转轴的转动角速度也是可以获知的，火箭弹的相对离轨速度更是可以依据火箭弹本身动力特性进行计算，故依据式(20)可求解出每一枚火箭弹的绝对离轨速度，得到绝对离轨速度后通过相关计算可以获得离轨时刻的攻角、侧滑角、弹道偏角和弹道倾角等运动参数，从而为空间弹道计算提供初始条件。设计中，可针对几种较为理想的离轨参数对弹体质心至回转轴的矢径、发射装置的转动速度以及弹体自身动力特性进行优化与组合。对于已经设计定型的火箭弹来说，虽然弹体自身动力特性已经固定，仍可通过改变发射装置的设计与运动形式来改变火箭弹的离轨参数，从而获取较为理想的离轨参数，使火箭弹具有较好的空间弹道。

3.2 离轨时刻的攻角、侧滑角、弹道偏角、弹道倾角

火箭弹速度矢量与地面坐标系OgXgYg平面的夹角为弹道倾角θ，将火箭弹绝对离轨速度投影到在弹体坐标系中，各向分量写为矩阵形式：

(21)

(22)

弹体速度矢量V在纵向对称面上的投影与弹体纵轴之间的夹角即为攻角α:

(23)

速度方向与弹体轴线在水平面内的夹角为侧滑角β:

(24)

弹体速度矢量V与地面坐标系OgXgYg平面的夹角为弹道倾角θ:

(25)

弹体速度矢量V与地面坐标系OgXg轴的夹角为弹道偏角ψc:

(26)

3.3 火箭弹离轨角速度ωt

将离轨角速度ωt投影至弹体坐标系中。

(27)

式中：ωxt、ωyt、ωzt为弹体绕质心转动的角速度在弹体坐标系中的各向分量;ωxs、ωys、ωzs为定向器转动角速度在随动坐标系中的各向分量，定向器转动角速度在随动坐标系中表示为[0,ωh,ωf];ωz为火箭弹沿定向器的螺旋导槽运动时引起的弹体自转角速度;ωxz、ωyz、ωzz是ωz在弹体坐标系中的各向分量，在弹体坐标系中ωz为[ωh,0,0]。

4 两种特殊跟踪运动下的离轨参数

对目标进行跟踪时，随动控制系统需将射向或火箭弹速度的方向指向目标或目标前置点，调炮时发射装置绕俯仰和方位回转轴的转动方程形式如式(11)所示，转角φ是时间t的单值连续函数。上一节对火箭弹离轨参数表达式的推导是基于一般转动方程的，没有限制发射装置的转动形式，故推导得到的离轨参数表达式是通用的，在应用至实际工程中，需要根据发射装置具体转动形式，将离轨参数表达式进行具体化。在实际工程中，发射装置匀速绕轴转动和匀变速绕轴转动是常用的两种调炮方式，对两种运动方式下的火箭弹离轨参数进行研究很有必要。针对实际应用需求，本节将对火箭弹离轨参数表达式进行细化，以满足工程使用，研究时同样将这两种调炮运动简化为发射装置绕俯仰轴和绕方位轴的转动。

4.1 发射装置作匀速跟踪运动

发射装置绕俯仰回转轴作匀速转动时的方程为:

(28)

式中：φf0为t=0时φf的值;n1为周期。

发射装置绕方位回转轴作匀速转动时的方程为:

(29)

式中：φh0为t=0时φh的值;n2为周期。

将ωf和ωh分别代入式(20)和式(27)，则发射装置作匀速转动时火箭弹的绝对离轨速度和离轨角速度可表示为:

(30)

(31)

式(30)和式(31)分别为发射装置匀速转动时火箭弹绝对离轨速度和离轨角速度的表达式，与式(20)、式(27)相比可知，发射装置绕俯仰轴与绕方位轴的转动角速度均为定值，可用转动周期表示，使公式的计算得到简化。当发射装置作匀速转动时，可直接应用式(30)和式(31)计算相应的绝对离轨速度和离轨角速度。

4.2 发射装置作匀变速跟踪运动

发射装置绕俯仰回转轴作匀变速转动时的转动方程为:

(32)

式中：ωf0、φf0分别为t=0时的角速度和转角;εf为角加速度。

发射装置绕方位回转轴作匀变速转动时的转动方程为:

(33)

式中：φh0、ωh0分别为t=0时的转角和角速度;εh为角加速度。

将ωf和ωh分别代入式(20)和式(27)，则发射装置作匀变速转动时火箭弹的绝对离轨速度和离轨角速度可表示为:

(34)

(35)

式(34)和式(35)分别为发射装置匀变速转动时火箭弹绝对离轨速度和离轨角速度的表达式，与式(20)、式(27)相比，式(34)和式(35)针对发射装置的运动进行了细化，更为具体，可直接应用公式计算相应的绝对离轨速度和离轨角速度。

5 结 论

本文主要对防空火箭炮作跟踪运动时发射的火箭弹离轨参数进行了研究，建立了适用于防空多管火箭炮的坐标系，完成了相关坐标系的转换，在简化发射装置绕俯仰回转轴和绕方位回转轴转动的基础上，推导了发射装置作跟踪运动时火箭弹离轨瞬间的运动参数表达式，能够根据火箭弹离轨时发射装置的转动速度、弹体质心至回转轴的矢径以及火箭弹自身动力特性计算相应的离轨参数，为火箭弹空间弹道解算提供了较为准确的初始条件。另外，针对防空火箭炮常用的匀速跟踪运动与匀变速跟踪运动，将火箭弹绝对离轨速度和离轨角速度表达式进行了细化，为实际工程应用提供了参考。

参考文献(References)

[1] 徐明友.火箭外弹道学[M]. 北京: 国防工业出版社, 1980．

XU Ming-you. Exterior ballistics of rockets[M]. Beijing:National Defense Industry Press, 1980．(in Chinese)

[2] 姚昌仁. 火箭导弹发射装置设计[M]. 北京: 北京理工大学出版社, 1998．(in Chinese)

YAO Chang-ren. Design of rocket and missile launching device[M]. Beijing: Beijing Institute of Technology Press, 1998．(in Chinese)

[3] 李强, 薄玉成, 朵英贤．转管炮旋转发射惯性对弹丸起始扰动的影响分析[J]. 弹道学报, 2005, 17(4): 88-92．

LI Qiang, BO Yu-cheng, DUO Yin-xian. Influence of rotating effect on initial bullet disturbancein gatling guns[J]. Journal of Ballistics, 2005, 17(4)：88-92．(in Chinese)

[4] 陈阵, 毕世华, 刘广璞, 等. 火箭弹初始扰动实验研究[J]. 固体火箭技术, 2010, 33(1): 112-114．

CHEN Zhen, BI Shi-hua, LIU Guang-pu, et al. Exper imental research on initial disturbances of rocket[J]. Journal of Solid Rocket Technology, 2010, 33(1): 112-114．(in Chinese)

[5] 戴耀, 汪德虎. 舰艇运动对舰炮起始发射条件的影响[J]. 火炮发射与控制学报, 2002(3): 9-12．

DAI Yao, WANG De-hu. Influense of warship motion to naval gun initiative shoot condition[J].Jourmal of Gun Launch & Control, 2002(3): 9-12.(in Chinese)

[6] 韩雁飞. 舰空导弹发射模型研究[J]. 舰载武器, 2001(4): 12-16．

HAN Yan-fei.Study on launch model of ship to air missile[J].Shipborne Weapons,2001(4):12-16．(in Chinese)

[7] 刘志明, 韩珺礼, 高敏. 火箭炮发射过程中火箭弹沿定向管运动分析[J]. 火炮发射与控制学报, 2003(2): 7-11．

LIU Zhi-ming, HAN Jun-li, GAO Min. Analysis of rocket movement along guided launcher during firing[J]. Joumal of Gun Launch & Control, 2003(2): 7-11．(in Chinese)