基于摄动法解决病态单纯形法的一点改进

王丽芳

(广州工程技术职业学院石化工程系，广东 广州 510726)

基于摄动法解决病态单纯形法的一点改进

王丽芳

(广州工程技术职业学院石化工程系，广东 广州 510726)

对一般的摄动法解决病态单纯形法的方法进行了改进，给出了简单的证明。

线性规划；摄动法；退化；基可行解；最优解

考虑下列线性规划问题：

mincx

s.t.Ax=bx≥0

(1)

式中，A是m×n矩阵，秩为m；b≥0。

在线性规划问题标准化以后，设系数矩阵的秩为m，变量个数为n，在基解或基可行解的概念中，n-m个非基变量都等于0，m个基变量由线性方程组惟一解出，一般为正分量，若有一个或一个以上基变量为0，则定义为退化情形，或称退化解。

现在使右端向量b摄动，令：

(2)

式中，ε是充分小的正数；pj是矩阵A的第j列。得到线性规划问题(1)的摄动问题：

mincx

s.t.Ax=b(ε)x≥0

(3)

下面证明，当ε取某些数值时，摄动问题(3)是非退化问题，并且可以通过求解摄动问题(3)来确定线性规划问题(1)的最优解或得出其他结论［1］。

定理1对于线性规划问题(1)，存在实数ε1≥0使得当0<ε<ε1时，摄动问题(3)是非退化的。

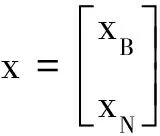
把式(4)按分量写出：

(5)

式中，J是非基变量下标集；xBi是基变量。

在B下，摄动问题(3)的基本解是:

(6)

把式(6)的右端可看作z的多项式：

(7)

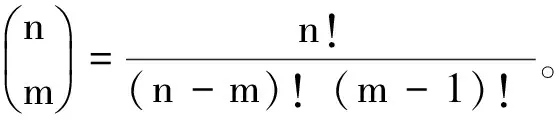
根据定理1，利用单纯形方法解摄动问题(3)时，不会出现循环现象。下面分析由求解问题(3)的结果能够给出线性规划问题(1)的最优解或给出关于线性规划问题(1)的解的状况的其他结论［3］。

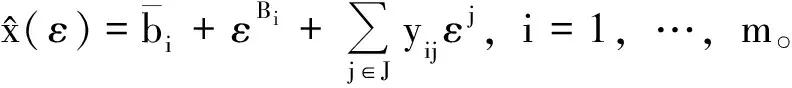
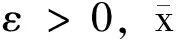
定理3若摄动问题(3)没有可行解，则线性规划问题(1)也没有可行解。

定理4若对充分小的ε>0，摄动问题(3)是无界问题，则线性规划问题(1)也是无界问题。

综上所述，摄动问题(3)当ε充分小时一定是非退化的，因此能够避免循环现象，并且通过求解摄动问题(3)一定能给出线性规划问题(1)的解答。这样，从根本上解决了可能发生的循环问题。

例1

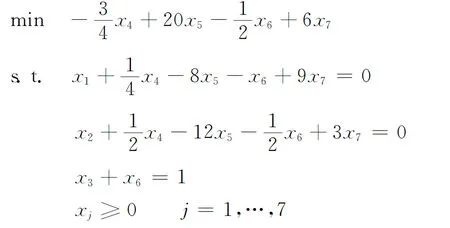
初始单纯形表如表1。取第4列为主列，先比较多项式的零次项的系数，再比较一次项的系数，即第1列中第1行及第2行的元素分别除以主列(第4行)中对应的正元素，取其最小比值(最小值为2),于是取表1第2行为主行，主元为12，经主元消去得到如表2的单纯形表。

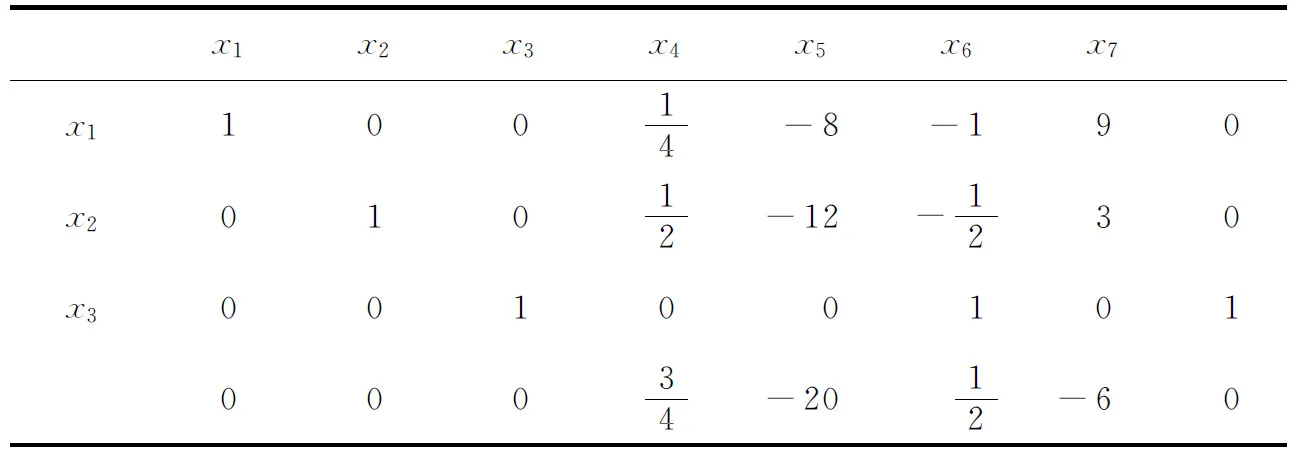
表1 初始单纯形表

再以表2中以第3行为主行，主元为1，经主元消去得到如表3的单纯形表。

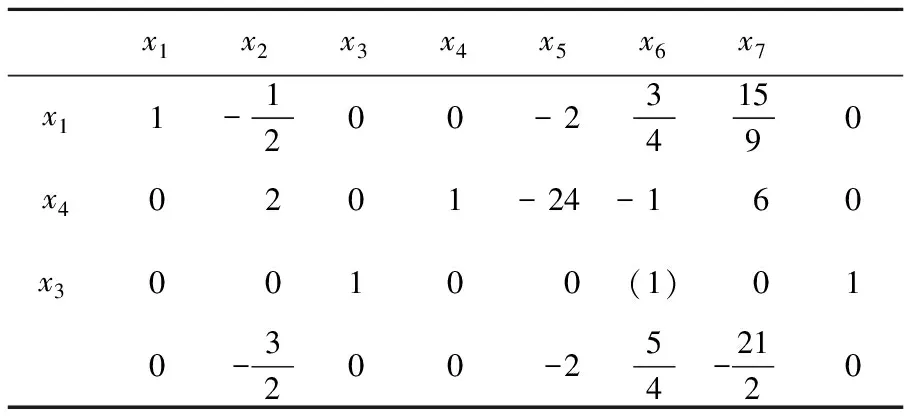
表2 以第2行为主行消去主元后的单纯形表

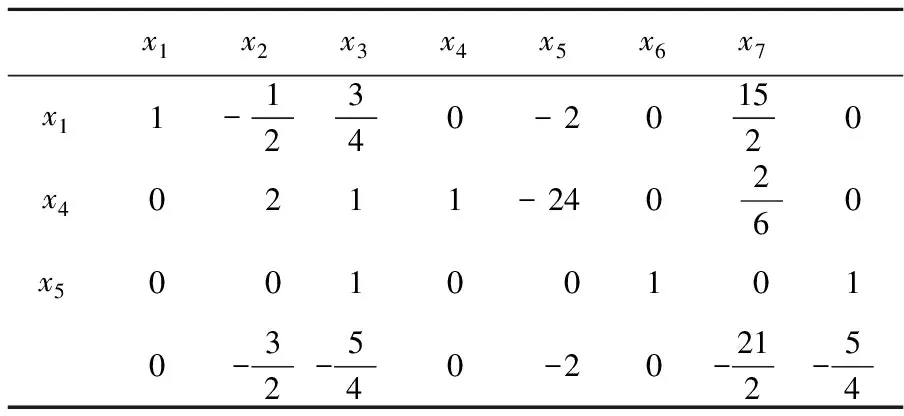
表3 以第3行为主行消去主元后的单纯形表

经2次迭代得到最优解和目标函数最优值：

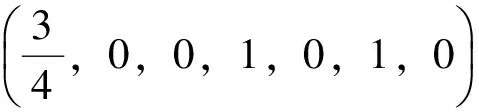
例1是一个退化问题，即存在退化问题的基本可行解，用一般单纯形方法求解时出现循环现象，而采用摄动法就成功地避免了循环的发生。

［1］徐成贤.近代优化方法［M］.北京:科学出版社，2009.

［2］ 袁亚湘,孙文瑜.最优化理论和算法［M］.北京:科学出版社,1997.

［3］ 中国人民大学数学教研室.线性规划［M］.北京:中国人民大学出版社，1988.

10.3969/j.issn.1673-1409(N).2012.07.003

O224

A

1673-1409(2012)07-N005-03

2012-04-16

王丽芳(1966-),女，1987年大学毕业,高级讲师,现主要从事最优化方法方面的教学与研究工作。

［编辑］ 洪云飞