汶川震源有限差分数值模拟研究

干大勇，赵晨露，张劲超，孟祥琦

(成都理工大学地球物理学院，四川 成都 610059)

汶川震源有限差分数值模拟研究

干大勇，赵晨露，张劲超，孟祥琦

(成都理工大学地球物理学院，四川 成都 610059)

2008年5月12日在四川汶川发生8.0级地震，震中位于龙门山断裂带上。地震激发的地震波可以用来研究震源破裂过程及地球内部的层次结构。对地震台站接收到的地震记录的拟合图重新进行了拟合，得到一个极易用数学式表达的震源时间函数，并结合龙门山的实际情况，划分为碎屑岩层、碳酸盐层及基底层模拟区域，并运用交错网格的有限差分法对声波方程进行数值模拟。研究表明，利用3个不同初始震源都能得到较好的波场快照图，而初始震源持续时间短的波场快照精度更高；不同初始震源不同地层的单点P波形图都能与根据地震台站接收记录拟合的P波形图相符合。因此，通过数值模拟能够反映汶川地震波传播的相关特征。

有限差分；声波；数值模拟；汶川震源

有限差分法长期以来是求取微分方程数值解的一个主要方法，也是目前地震勘探资料数字处理中采用的求解波动方程的主要方法。波动方程有限差分法正演模拟，对认识地震波传播规律、进行地震属性研究、地震资料地质解释、储层评价等，均具有重要的理论和实际意义。以波动方程为基础的有限差分法能够准确的描述地震波在地下复杂介质中运动学和动力学特征，对地震波的波场特征和传播规律能够进行完整的描述。笔者主要以二维声波方程为基础，分析有限差分数值模拟中的频散和边界条件，对汶川地震激发的地震波传播进行数值模拟。

1 有限差分声波数值模拟

在二维空间域内的X-Z平面内，以X轴为水平轴，以Z轴为垂直轴，其二维二阶波动方程可以表示为：

(1)

式中，c0为传播速度，m/s；u为位移函数，m。

根据均匀弹性各项同性介质速度、应力、位移3个场变量以及场变量关系方程，不考虑剪应力的影响并令其为零，将二阶方程转变为一阶方程：

(2)

式中，Vx、Vz分别为质点振动速度的水平分量和垂直分量，m/s；ρ为介质密度,kg/m3；p为压力,Pa。

1.5 评价标准 无压红:受压部位皮肤与其他皮肤无变化;轻度压红:受压部位皮肤有红晕，解除压力后30 min可以自行消退;瘀红:受压部位皮肤瘀紫，解除压力后也无法消退，判定为压疮1期。

1.1 差分格式

采用经典的二阶差分格式对式(2)进行离散：

(3)

式中，k表示时间采样间隔,s；i表示X轴采样间隔,m；j表示Z轴采样间隔,m；Δx和Δz分别表示空间步长,m；Δt表示时间步长,s。

1.2 差分网格频散

不同频率的波分量以不同相速度传播时，会在声波方程有限差分数值解中存在差分网格频散。因此，在差分模拟中若对空间和时间步长取值不当会造成频散。对一种数值解法,需要知道计算稳定的离散参数区域,即分析解法的稳定性，据此笔者采用Courant的稳定性条件[3]:

1.3 完全匹配吸收边界

对式(2)引入人工边界条件，得完全匹配层方程为：

(4)

式中，dx、dz分别为x、z方向的衰减系数。

波长按传播距离进行衰减时衰减速度很快。当衰减吸收系数随空间位置变化时，不会在介质中产生任何反射。衰减吸收函数采用Collino[4]与Berenger J[5]等提出的通式：

(5)

式中，i代表从模型镶边后的外边界到有效模型区域内边界的网格点序号；PML代表完全匹配吸收层沿坐标轴方向所占的网格点个数；m代表吸收衰减系数的阶数；B为衰减幅度因子。

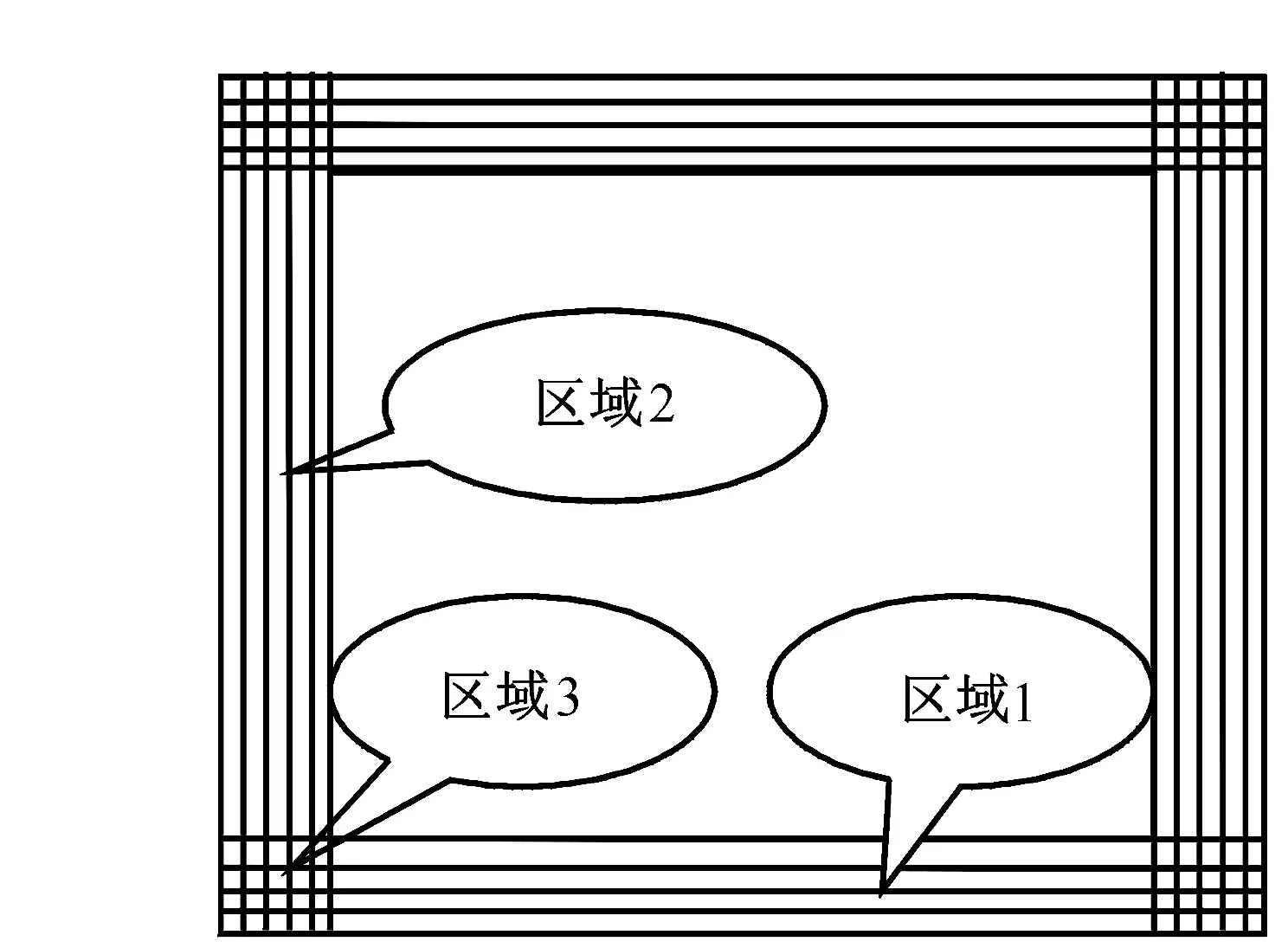
图1 完全匹配层吸收边界

完全匹配层作为吸收边界的基本原理是在研究区域内四周加入人工边界。图1所示为在加入的完全匹配层中分为3个区域(在区域1令dx=0,dz≠0；在区域2令dz=0,dx≠0； 在区域3令dx≠0,dz≠0)。当波传播到完全匹配层的边界时按距离的指数衰减，数值也越来越近似为零，这就不会产生边界反射。

2 初始震源

声波方程数值模拟初始震源设置为与汶川地震震源相类似的震源。图2所示为汶川地震发生时某地震台站接收到的地震记录拟合的时间持续图。

根据以上拟合的汶川地震震源时间图形，通过计算，拟合出一条近似的曲线图来模拟汶川震源(见图3)。

3 数值计算与分析

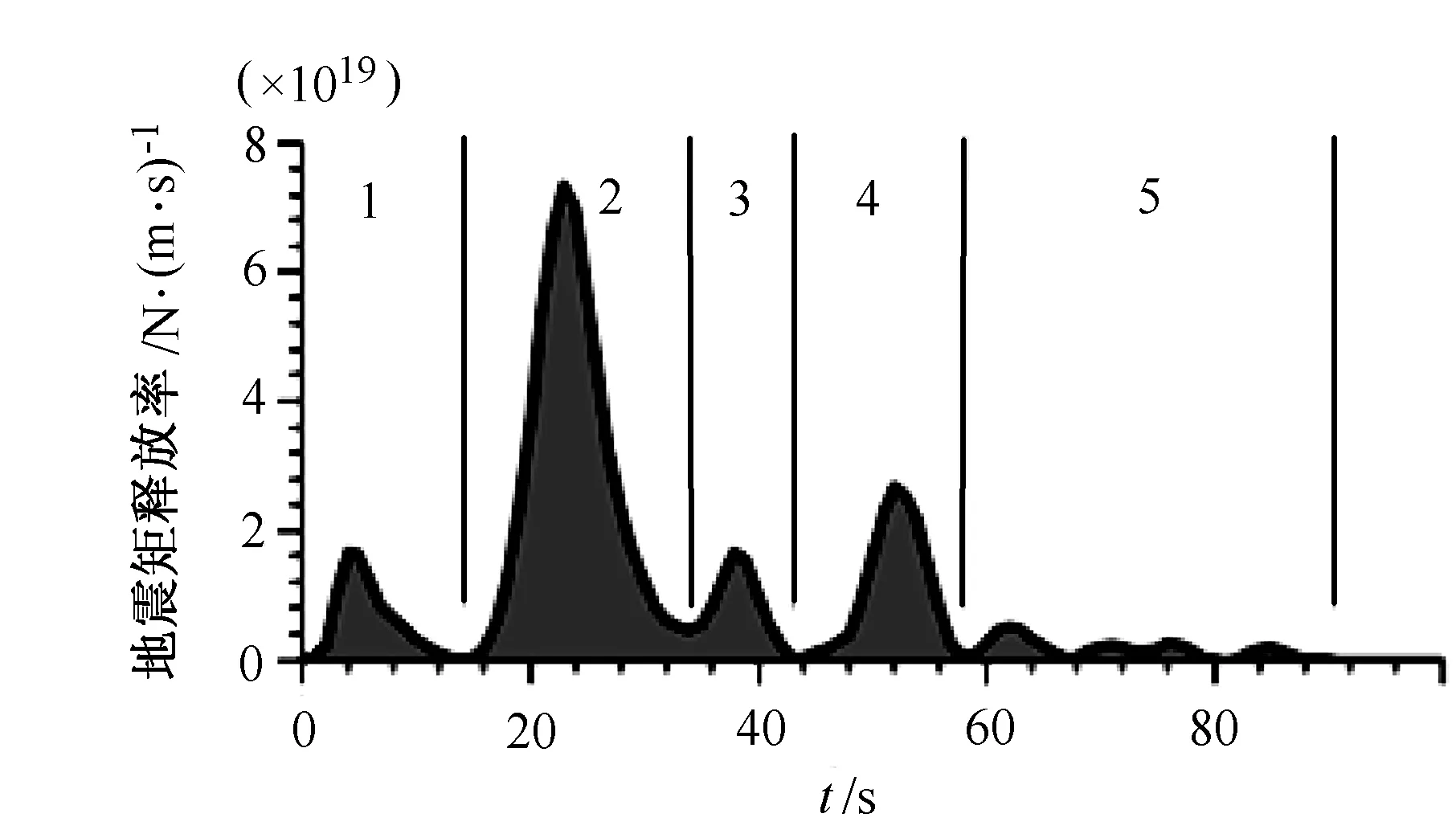
图2 汶川地震震源时间函数

数值模拟中尽量与汶川地震实际情况相符合，震源设置在13.5km处，模拟区域为24km×24km，对整个区域分为3个不同介质模型，分别为碎屑岩层0～5km、碳酸盐岩层5～9.6km和基底9.6～24km(见图4)。

模拟模型大小为600×600个网络，网格间距空间Δx=Δy=40m，时间步长Δt=0.01s,分别用3种不同初始震源对声波方程进行数值模拟。

3.1 利用声波方程模拟不同时间的波场快照

1)以图3(a)震源为初始震源 以图3(a)震源为初始震源进行的声波方程模拟时不同时间的波场快照如图5所示。当t=2s时，地震波已从基底传播到碳酸盐岩层(见图5(a))；t=4s时地震波已到达碎屑岩层，并且在碎屑岩与碳酸盐岩的分界面存在界面反射(见图5(b))；t=5.6s时地震波传播到地表(见图5(c))。由于加入了边界细搜条件，人工边界反射不是很明显。

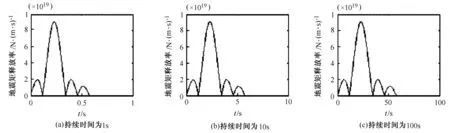
图3 拟合近似的地震震源时间函数

图4 数值模拟区域

2)以图3(b)震源为初始震源 以图3(b)震源为初始震源进行的声波方程模拟时不同时间的波场快照如图6所示。地震波由一介质传入另一介质时都存在界面反射，由于地震波在6s内是连续传播的，所以在短时间内界面反射现象不是很明显。由于存在边界反射，已经影响了地震波传播，因而在6s后会看到明显的边界反射效果(见图6(a)和图6(b))。在t=5.6s时已经开始有明显的边界反射出现，并且地震波的前波已到达地表(见图6(c))。当地震波主波到达地表时，在碳酸盐岩层和基底出现明显的边界反射(见图6(d))。

图5 以图3(a)震源为初始震源进行的声波方程模拟时不同时间的波场快照

图6 以图3(b)震源为初始震源进行的声波方程模拟时不同时间的波场快照

图7 以图3(c)震源为初始震源进行的声波方程模拟时不同时间的波场快照

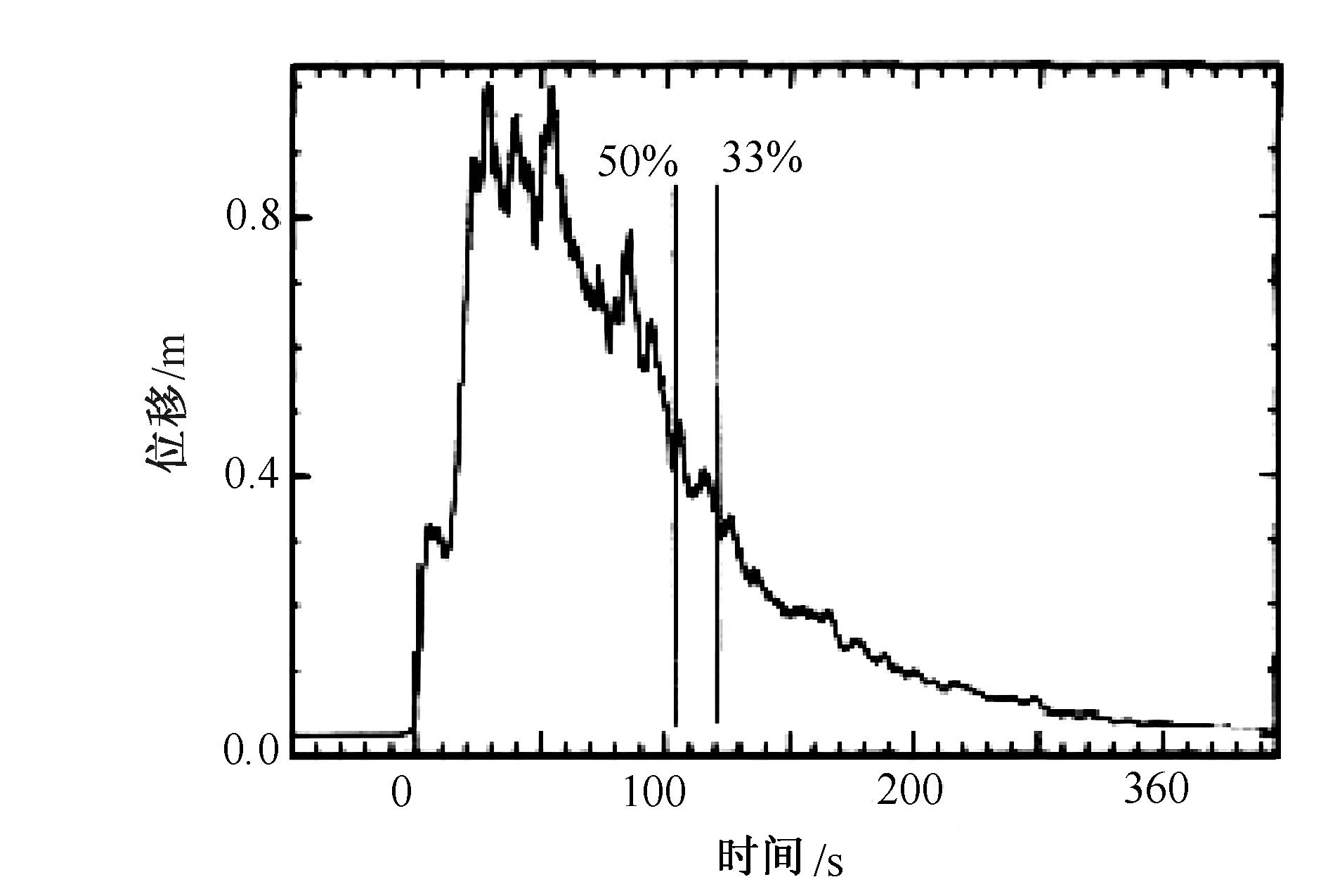
图8 根据地震台站接收到的记录拟合的P波形图

3)以图3(c)震源为初始震源 以图3(c)震源为初始震源进行的声波方程模拟时不同时间的波场快照如图7所示。地震波前波到达地表(见图7(a))，地震波主波已经开始出现(见图7(b))，第3次波出现(见图7(c))，第4波出现(见图7(d))。在对以上数值模拟的基础上，选择3个不同介质的点，给出其P波形图，并与地震台站接收到的记录拟合的P波形图(见图8)进行比较。

3.2 震相模拟

1)以图3(a)为初始震源 以图3(a)为初始震源模拟得到的各点P波形图如图9所示。由图9可知，当持续时间为1s时，由于时间短精度高，在短时内单点P波形图效果较好，因而能更好地描述地震波的传播特征。当波传播到各界面出现边界反射导致负值，随着时间推移振动逐渐停止。

2)以图3(b)为初始震源 以图3(b)为初始震源模拟得到的各点P波形图如图10所示。由图10可知，当持续时间为10s时，单点P波形图与地震台站接收到的地震记录拟合的P波形图最为相似,说明时间和空间的精度影响的频散最小,从而更能反映地震波在地层的传播形态，且随着时间的推移该图形会趋于平稳。

3)以图3(c)为初始震源 以图3(c)为初始震源模拟得到的各点P波形图如图11所示。由图11可知，当持续时间为100s时，虽然计算效率降低了，但更能结合实际情况，很好地反映了地震波的特征。

总之，通过计算模拟得到的P波形图与地震台站接收到的地震记录拟合的P波形图大致相似，说明上述方法能够较准确地反映地震波在地下的反射、透射、散射等传播形态和各种复杂的运动学和动力学特征。

4 结 语

根据3层地质模型，通过稳定性条件与边界条件的约束，利用3种不同持续时间的汶川初始震源进行声波方程数值模拟，并将模拟结果与根据地震台站接收的地震记录拟合的P波形图对比。研究表明，利用3个不同初始震源都能得到较好的波场快照图，而初始震源持续时间短的波场快照精度更高；不同初始震源不同地层的单点P波形图都能与根据地震台站接收记录拟合的P波形图相符合。因此，通过声波方程的有限差分数值模拟能够反映地震波在地层的传播特征。

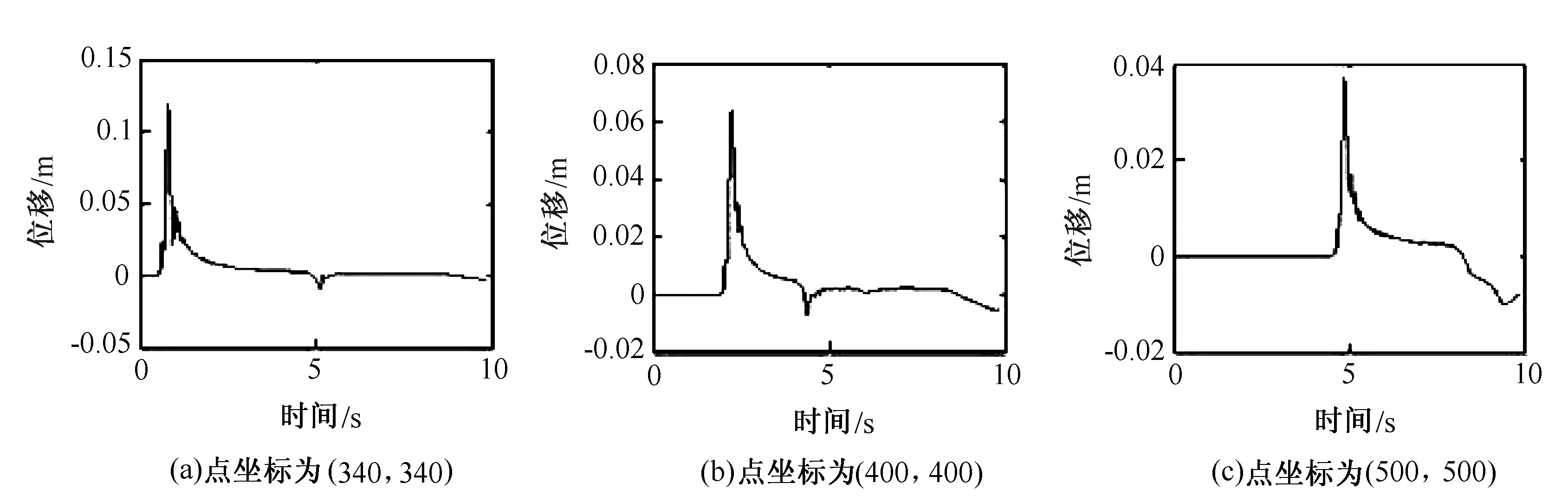
图9 以图3(a)为初始震源模拟得到的各点P波形图

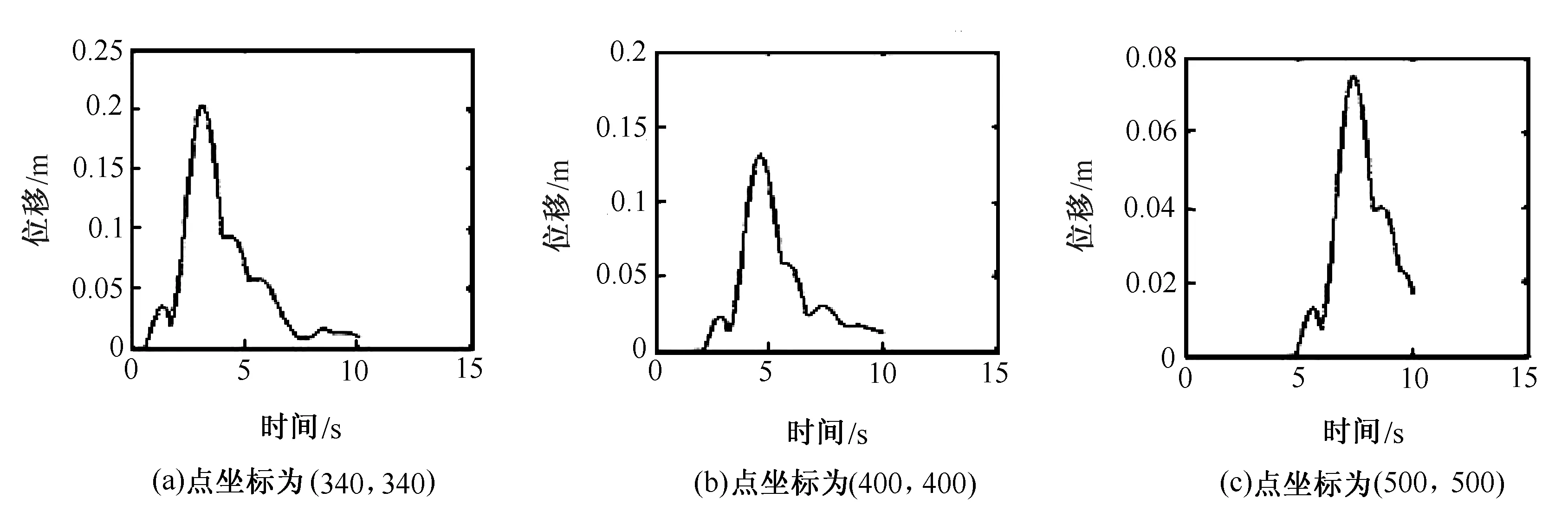
图10 以图3(b)为初始震源模拟得到的各点P波形图

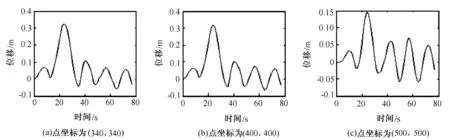
图11 以图3(c)为初始震源得到的各点P波形图

[1]王卫民,赵连峰,李娟，等.四川汶川8.0级地震震源过程[J].地球物理学报，2008，51(5):1403-1410.

[2]严珍珍,张怀,杨长春，等.汶川大地震地震波传播的谱元法数值模拟[J].中国科学，2009，39(4):393-402.

[3]Collina F,Tsogka. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J].Geophysics,2001,66(1):294-307.

[4]Zakaria A, Penrose J. The Two Dimensional Numerical Modeling Of Acoustic Wave Propagation in Shallow Wate[J].Austrialian Acoustical Society Conference,2000,15:1-5.

[5]Berenger J.P A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics，1994,114(2):185-200.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.10.019

P315.3

A

1673-1409(2012)10-N060-05