由一堂平面向量课所引发的思考
2012-11-20诸暨中学浙江诸暨311800
● (诸暨中学 浙江诸暨 311800)
由一堂平面向量课所引发的思考
●俞建锋(诸暨中学 浙江诸暨 311800)
教学活动具有复杂性和多变性,因此精心的预设是上好一节课的基础.认真钻研教材,全面了解学生,有效开发资源是预设的重点.但在实施课堂教学的过程中,教师如何处理“预设”与“生成”的关系,直接关系到学生的学习效果.本文结合笔者的一个教学案例,对如何处理“预设”与“生成”的关系谈几点看法.
1 一道例题的2种教学生成
以下是笔者的一次课堂教学经历:同一道例题,教师具体讲授于甲、乙2个不同班级(平行班).虽然是基于同一预设的一道习题的教学,其教学过程却“意外”地显著不同.
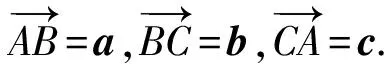
甲班的教学片段:
师:证明正三角形的方法有哪些?
生(齐声):3条边相等或3个角相等.
师:用向量如何刻画呢?
生A:利用|a|=|b|=|c|即可.
生B:或许可以利用∠A=∠B=∠C,因为a·b=|a|·|b|cosθ(θ为a,b的夹角)中也有角.
师:好!下面我们来试试.
(学生说,笔者板书.)

图1
证法1如图1,可得
a+b+c=0.
又因为
a·b=b·c,
所以
a·b-b·c=b·(a-c)=0,
即 (-a-c)·(a-c)=0,
亦即
(a+c)·(a-c)=0,
从而
a2-c2=0,
即
|a|2=|c|2,
亦即
|a|=|c|.
同理可得
|b|=|c|,|a|=|b|,
从而
|a|=|b|=|c|,
因此△ABC是正三角形.
笔者小结:解决本题的关键是利用a+b+c=0得到b=-a-c,又由a·b=b·c得到b·(a-c)=0,综合得到结论.
至此,仅用7分钟时间便完成了该例题的讲授,笔者认为目的已经达到,教学继续进行,按预先的教案讲解例2~例5,按部就班直至下课.
乙班的教学片段:
和甲班类似,当笔者提问完“用向量如何刻画呢?”,学生这样回答:
生A:构造直角三角形,利用斜边上中线的性质.
生B:利用|a|=|b|=|c|.
师:请生A、生B在黑板上板演,其他学生在下面思考.
生A板演:
证法2因为a+b+c=0,
所以
a·a=(b+c)·(b+c),
从而 |a|2=|b|2+|c|2+2b·c,
(1)
同理可得
|b|2=|a|2+|c|2+2a·c,
(2)
式(1)-式(2)得
|a|2-|b|2|=|b|2-|a|2+2(b·c-a·c).
又因为
a·b=b·c=a·c,
所以
|a|2-|b|2=|b|2-|a|2,
即
|a|2=|b|2,
亦即
|a|=|b|.
同理可得
|b|=|c|,|a|=|c|,
从而
|a|=|b|=|c|,
因此△ABC是正三角形.
生B板演:
证法3因为a·b=b·c=a·c,
所以
a·b-b·c=b·(a-c)=0,
从而
b⊥(a-c).
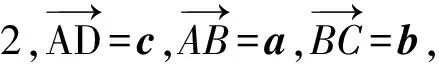

图2

又因为|AC|=|AD|,所以AB是DC边上的中线,因此
|AB|=|AC|=|AD|,
即
|a|=|c|.
同理可得
a⊥(b-c),
进而
|b|=|c|,
从而
|a|=|b|=|c|,
因此△ABC是正三角形.
笔者讲评:学生A抓住了|a|2=|b|2+|c|2+2b·c,该式好似解题的一个“中转站”,起到了纽带的作用(学生欣喜).学生B构造直角三角形,并利用斜边上的中线这一想法,恰倒好处.
至此,本例的教学似乎应该结束,而且课堂用时超过21分钟(较甲班多了14分钟).笔者不经意地发问”有不同解法吗?”这一问又激起了学生思维的浪花.
生C:我利用几何法做的,利用菱形对角线垂直的性质.
笔者放弃原先准备的教案,让学生继续交流.
师:请学生C到黑板上展示自己的过程,其他学生自己思考.
(此时教室内一篇寂静,大家已不满足于一种解法.)
学生C的板演:


图3


所以四边形ABCD为菱形,从而
|AB|=|AC|,
即
|a|=|c|.
同理可得|a|=|b|,|b|=|c|,
从而
|a|=|b|=|c|,
因此△ABC是正三角形.
师:学生C的解法可以说是另辟蹊径,妙不可言.还有不同的方法吗?
笔者话音刚落,学生E便回答自己是利用a+b+c=0得到b=-a-c,又由a·b=b·c,得到b·(a-c)=0,综合得到结论.(这可是教师完成“教案剧”千呼万唤的方法!)
学生E已显得迫不及待:
证法5由于a+b+c=0,所以
a·b=(b+c)·(a+c)=
a·b+a·c+c·b+c·c2,
从而
c2=-(a·c+b·c),
同理可得
a2=-(a·b+a·c),b2=-(b·a+b·c).
因为
a·b=b·c=a·c,
所以
|a|2=|b|2=|c|2,
即
|a|=|b|=|c|.
师:巧妙地利用了a+b+c=0,不易想到,也不失为一种好思路.
下课铃声响了,还有学生在不断地思考……
新课堂是活动的课堂,讨论、合作、交流的课堂,它呼唤着学生的积极参与,因此,教师要善于把握时机,创设问题情景,激发学生潜能,要善于将“球”踢给学生,引导学生去质疑、发现和探索.教师要相信青年学子的潜能是不可估量的,要改变教师的角色.教师要悄然“换岗”,变传授者为引导者、组织者、合作者;学生要自然“上岗”,变被动听为主动探求.只有充分地体现出学生的主体性、主动性,教师的主导作用才能得到充分发挥.
2 对教学预设与课堂生成的思考
同一个例题的教学过程相差如此之大,着实发人深思,这是一场“教案剧”.教师是“强迫”学生按照课前的预设学习,还是增强“随意性”,尽量按照学生的认知情况生成?该如何处理“预设”与“生成”的关系呢?
(1)教学预设要给学生留有足够的自由思考的空间.
探究学习具有自主性、过程性、实践性、开放性等基本特征[1],因而探究教学更加重视学生的主体地位,教学的重心不是教师的教,而应当是学生的学.在课堂情境下,学生通过讨论、质疑、交流、反思、探究等认知和实践活动,会产生很多非预设的问题,探究的方向、方式、过程等也会与教师的预设大相径庭.这就需要教师灵活处理预设与生成的关系,充分关注学生课堂生成的特点,给学生的探究保留足够的自由空间,顺势而为,动态调整,使教学预设随着课堂进程不断改变和重建,保证个体知识的自主建构和逐步完善.本文所述的案例中,在甲班,教师“及时地”中断了学生的不同想法,强硬地执行了课前的预设,牵着学生向前走,貌似很节省时间,也完成了所谓的“任务”,但是和乙班的情况相比,思维的积极性、思考问题的灵活性、解决问题的能力诸方面都是无法比拟的.可见,在教学预设时,要给学生的自主思考留有足够的空间,否则,学生的主体地位无法真正体现.
(2)课堂生成与课前预设的不一致正是激发学生创新思维的起点.
“生成”对应于“预设”.尽管在课前的设计,教师对学生可能出现的一些情况做了设想,然而面对的学生是千变万化的,他们的真实水平往往无法准确估计,更多时候与预设有差异甚至截然不同.当教学不再按预设展开,这就需要教师冷静思考,巧妙捕捉其中的亮点资源,并灵活地调整教学方法,机智生成新的教学方案.笔者在甲班的教学实施过程中,对学生回答的不同想法没有重视,而是尽可能将学生的思路拉回到教师预设的轨道上来,生硬地执行了课前预设的思路.但乙班的情况表明,当学生的思考与教学设计不一致时,就是激发学生创新思维的好时机.
苏霍姆林斯基曾描述这样的课堂:“有些教师能够做到使他的每一位学生在课堂上都取得进步.……在这里,充满着……师生间相互体谅的气氛,有一种智力受到鼓舞的精神,每一位学生都在尽量靠自己的努力去达到目的.你从儿童的眼光里就能看那种紧张地、专心致志地思考的神色:一会儿发出快乐的闪光(正确答案找到了!)一会儿又在深沉地思索(从哪里入手来解决这道应用题呢?)教师在这样的气氛里工作是一种很大的享受.”[2]这也是教师心目中所希望出现的数学课堂情形!通过2节课的对比,不难看出,乙班学生的“好想法”层出不穷,而这种情形正是教师恰当处理预设与生成的关系、及时抓住激发学生创新思维的好时机,使得教学过程向着理想课堂的方向发展.
(3)预设是为了生成,而生成是动态的.
教学目标的综合性决定了师生活动的多样性和教学环境的复杂性.教师必须把开发学生潜能作为教学最重要的任务,必须意识到学习是不可重复的,是激情与智慧的综合生成过程.因此,教师应根据课堂教学的“预设”,给学生腾出空间,让学生在共同探究中享受“生成”.前文所述的案例中,笔者在甲班教学时,生硬地将教学生成变成了课前预设的固定结论,而在乙班的生成过程是动态的、不断调整的,2个班学生的收益有着明显的差异.
教师在备课进行教学预设时,就应当多角度考虑问题的各种可能性,这样教师在面对学生的不同想法时,能更迅速地形成教学设想,从而保证在实施过程中根据教学的进程,不断调整自己的教学行为.当然,学生的想法教师课前未必想到,因此,教师充分采纳学生的想法,实际的课堂生成就未必是教师提前预设的情境.换言之,教学生就变成了一个动态的过程,这样新课改数学教育所期待的“走向未知”的“后现代教育观”与“对话课堂观”的动人景象就一定会出现!
[1] 贝尔.中学数学教育学[M].许振声,译.北京:教育科学出版社,1988:125.
[2] 苏霍姆林斯基.给教师的建议[M].杜殿坤,译.北京:教育科学出版社,1984:76.
