关于过程能力指数和不合格品率之间的关系研究

陶靖轩

（中国计量学院 经济与管理学院，浙江 杭州310018）

长期以来，工业生产过程的过程能力指数与产品不合格品率之间的关系研究是质量专业学术界和实际工作者关注的一个热点，人们热衷于寻找一个确定的模型用过程能力指数准确地换算产品不合格品率，但是很快就发现单靠一个过程能力指数（CP或CPK）很难表达出过程产品的不合格品率［1］；而给定某个过程产品的不合格品率也不能唯一确定过程能力指数.比如：针对过程分布中心和标准中心（规范中心）重合时的情况以及分布中心与标准中心不重合时的情况推导的相关数学模型：

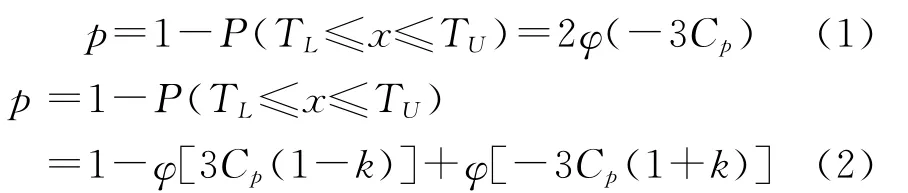
其中，TU、TL分别表示某产品规定的单一质量特性值上、下容差限，Cp表示中心重合算出的程能力指，k代表偏移系2ε／T（里T 指容差限度），p指某过程产品的不合格品率.

然而在生产过程中过程中心常常发生偏移，以上所说CP仅仅是一个理想化的过程能力指数（又称潜在的过程能力指数），当过程已经发生偏移时，利用偏移后的过程能力指数能否确定过程的产品不合格品率？两个生产过程产生了相同的不合格品率是否说明他们有相同的过程能力？这两个概念之间究竟是什么关系？本文对此进行讨论，就教于同行专家.以下首先从过程能力的基本概念说起.

1 过程能力的概念

过程能力人们常常称作工序能力，也有作者说［1］是因为近年将服务业质量管理引入质量管理，故改称过程能力.它被定义为过程满足客户期望的能力，过程能很好满足客户要求，就认为过程有能力；反之就说过程能力不足.仔细地说是指过程加工质量方面的能力，它是衡量过程加工一致性的准绳，是稳态下的最小波动［3］.

当过程处于稳态时——也即处于受控状态，这时我们认为过程一般只受随机因素影响，而随机因素一般可以认为是相互独立的，他们的合成也具有随机性的性质，考虑到极限定理的约束作用，质量特性值的波动常常按正态分布处理.1951年美国统计学家费根堡姆（Feigenbaum）和朱兰（Juran）给出了过程能力的量化定义：即用6倍过程标准差描述过程内在的波动——用6西格玛作为过程能力的测度.在正态分布前提下，Kane（1989）、Montgomerg （1991）、Wheeler And Chambers（1992）、Wheeler（1998）给出了更一般的定义，即处于统计控制状态下（统计稳态）的过程覆盖过程分布中心99.73%的宽度.

以上定义可以说主要表达了过程的“声音”（Voice of process），并没有将过程能力与过程加工产品的规范（规格—也即客户期望）直接联系起来，而产品的不合格品率p是与以规格为标准的量化指标，所以它也无法与过程能力建立量化的关系模型.

当然这并不能说，过程能力B＝6西格玛与不合格品率p没有关系，从理论和实践两方面分析，B＝6西格玛越小，过程质量能力越强，由此过程生产的产品不合格品率应该越低.

早在1991年，Carr就提出将期望不合格率（不合格品率之比——作者注）作为过程能力指数，用观测值来估计.Yeh Bhattacharya提出了两个新过程能力指数，一个是用期望的不合格品率与实际的不合格品率（不合格品率观测值）的比值p0／.另一个过程能力指数是：

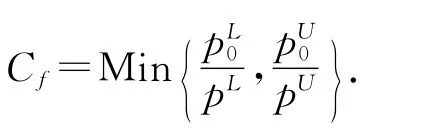
其中，上标L、U分别表示X 是小于LSL（的不合格品率），还是大于USL（的不合格品率）.但这两个过程能力指数只不过是从不合格品率符合程度的角度观察过程能力，与本文所述过程能力不是一个概念.

2 过程能力指数

朱兰（Juran）1961年用过程波动B与规格长度T来决定是否改进过程，从而使过程的波动B和规格极限（规范限，也即加工产品质量特性值合格与否的标准）紧密联系起来，从而使B与产品的不合格品率p建立了某种联系.重大的突破是1974年，Juran提出了过程能力比这一过程波动与过程规范（规格）相比的标准.从此之后，各种关于过程能力的研究全面展开，尤其是近20年间美国、日本、中国、英国等国家至少发表了500多篇相关的学术论文，一大批学者修改了过程能力假设的前提，向非正态、非对称公差、多元化等方向发展.但是，这些研究不论做了多少改进，其基本的研究模式并未脱离能力比这一框架.

传统的过程能力指数计算要求满足四个基本条件：（1）过程处于稳态，没有异常因素出现，也没有发生漂移和震荡.因此对于需要评价的对象过程，应首先判断是否处于稳态，只有稳态才能计算过程能力指数；（2）过程观测的产品质量特性值服从正态分布（本文不涉及非正态分布情形）；（3）样本具有代表性而且相互独立；（4）规范限能够准确地反映顾客要求.在此前提之下，最早（Kane 1986）提出的过程能力指数是：

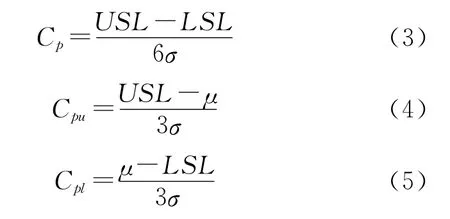
（4）式（5）式称为单侧过程能力指数，综合（4）、（5）人们规定了CPK即第二代过程能力指数：

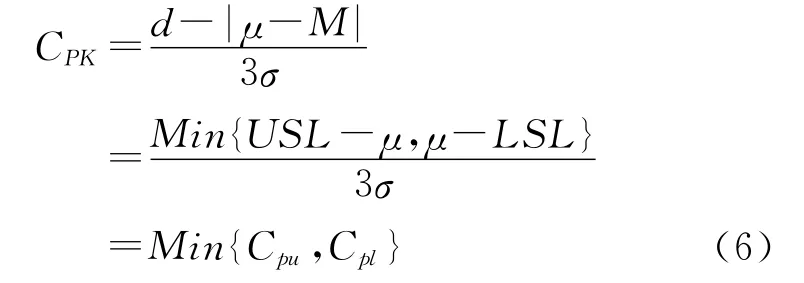
从式（1）人们可以在中心重合的理想条件下由过程能力指数CP唯一确定过程产品的不合格品率，而利用（6）的派生公式则有：

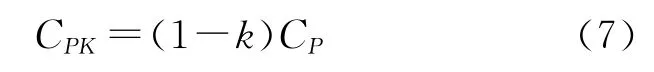
由此可得：

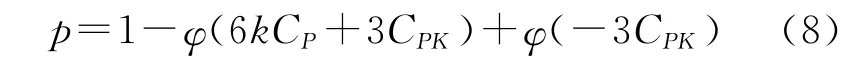
但是公式（8）并不是CPK与p的直接对应关系；换言之，给定CPK不可能唯一确定过程产品的不合格品率（详细的论述请参看文献［5］）；他们的具体关系是利用CPK推断出了过程产品的不合格品率p的一个上界（详细推导请参看文献［7］）.

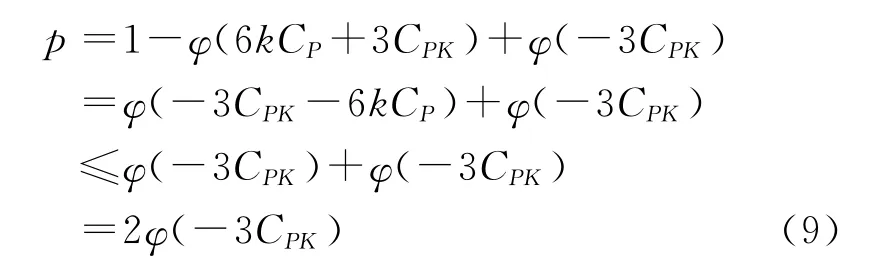
（9）式说明CPK提供了过程产品的不合格品率的一个上界，所以CPK（实际的过程能力指数）与CP相比更能反映实际的质量能力水平.而且由此我们知道了较强的过程能力（CP或CPK较大），不合格品率p至多不会超过上界2φ（-3CPK）.也就是说好的过程能力必将导致产品的合格品率1-p较高；而较高的产品合格品率1-p是好的过程能力的一个必要条件——或者说没有较高的合格品率1-p，就不可能会有较高的过程能力.

3 过程产品的不合格品率与过程能力指数的关系

现在我们提出另一个问题，过程产品的合格品率1-P较高，是否意味着一定是较好的过程能力呢？以下我们从两个方面进行讨论：

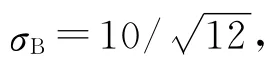
现在我们将A厂和B厂的产品进行比较，尽管A厂和B厂的产品都满足公差要求，甚至B厂产品的不合格品率比A厂还要小，但从质量水平来看，A厂却优于B厂，一个内行（专业）的采购人员如果想购买一批产品（而不是一个产品），一定会购买A厂的产品，因为A厂产品质量特性值小误差的比例比B厂高.其原因在于A，B两厂产品质量特性值分布性质有本质不同，A厂产品测量值近似服从正态分布，因此有更大比率产品接近理想目标值m0，在使用过程中其损失较小，也就是说有更高的质量水平，其生产过程有更强的工序能力.

2）在质量特性值为属性总体（比如只考虑产品是否合格品或不合格品）的离散情况下，如果我们研究总体的过程不合格品率P，假设也是对比两家工厂的产品，当其不合格品率相同情况下，能否说明他们有相同的过程能力（指数）呢？不能.因为这还应该看两个样本的大小——即样本量.单纯看不合格品率P1＝P2＝P是不能说明问题的，因为样本量如果不同（n1≠n2），那么两个样本的不合格品率p1、p2的抽样误差是不相同的：

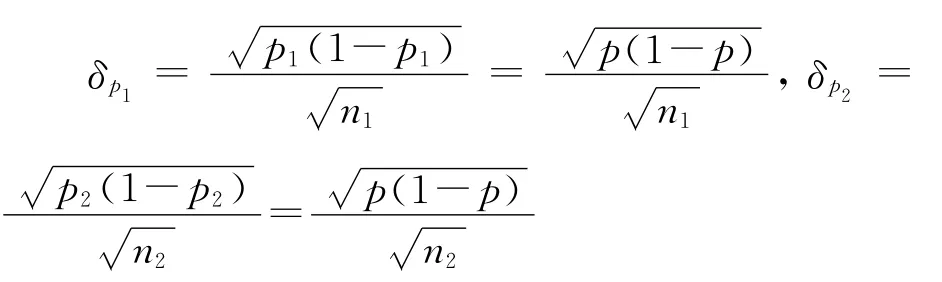
我们看到，样本量越大抽样标准误差就越小，这一不合格品率P就越稳定，过程能力就越强.

我们可以用下面的例子进一步说明这个问题：要比较两个优秀射手的能力水平问题，如果他们的命中率都是100%，而其中一个人是只射击一枪而碰巧命中，而另一个人是连续打了100枪，枪枪命中.显然，我们判断后者的命中水平应该更高一些，主要原因在于后者的射击水平发挥比较稳定，其击中能力是久经考验的.从统计学的角度看就是后者命中率的抽样标准误差更小.

4 结 语

综上所述，过程能力指数与过程生产的产品不合格品率是两个有密切联系同时又有本质不同的概念，过程能力指数是稳态情况下过程波动大小的相对测度，而不合格品率是将产品总体看作属性总体时不合格品数的结构（比重）相对数指标；通常用来表示符合性质量水平.它们都与性能指标的规范限发生联系，从不同的角度、不同的层面描述了过程的质量水平：好的过程能力（质量能力）可以保正产品的不合格品率限制在某一水平之下，也就是说好的不合格品率是良好的过程能力的必要条件，如果没有好的产品不合格品率，就不可能有较高的过程能力.

另一方面，仅仅能保证产品的不合格品率并不是过程能力好的充分条件；产品合格与否只不过是其质量特性值是否符合起码的规范限，而仅仅符合起码的规范限只是一个较低的要求，并不是说过程产品都达到了优质品的要求，不足以说明生产过程一定有好的过程（质量）能力.要提高产品的质量水平，不仅要尽最大努力降低产品的不合格品率，而且更需要查找分析波动产生的原因，采取措施加以消除，纳入标准，真正提高过程能力.

［1］王斌会，胡志萍，过程能力指数与不合格品绿的关系模型［J］.数理统计与管理，2007（1）：57-61.

［2］陶靖轩，刘春雨，张月义，等.六西格玛管理简明教程［M］.北京：中国计量出版社，2005：72-75.

［3］全国质量专业技术人员职业资格考试用书编委.质量专业理论与实务（中级）［M］.北京：中国人事出版社，2012：167-171.

［4］伍 爱.质量管理学［M］.广州：暨南大学出版社，99：135.

［5］陶靖轩，陈意华，宋明顺，等.关于过程能力分析的若干思考［J］.科技通报，2006（3）：34-37.

［6］SON S，KENT T，ZACKS S.现代工业统计：质量与可靠性的设计及控制［M］.北京：中国统计出版社，2002：378-380.

［7］陶靖轩，度量工业过程能力的重要指标CPK［J］.中国计量学院学报，2010（3）：63-69.