差分酉空时协作系统的多符号裁减自动球形译码

陈 婕，周小微，金小萍，韩新强，金 宁

（中国计量学院 信息工程学院，浙江 杭州310018）

为了解决多输入多输出（multiple input multiple output，MIMO）［1］系统在实现空间分集效果时，终端设备由于体积、硬件复杂度和功耗等限制的问题，提出了一种新的空间分集技术——协作技术［2-3］.在协作技术实现的过程中：一方面，发送信号的协作方式多样化，其中 AF［4］（amplifyforward放大转发）相比于 DF［5］（decode-forward译码转发）和 CC［6］（coded-forward编码转发）协作方式而言，复杂度低且易于实现；另一方面，对接收信号的译码方式也多样化，其中差分检测方式［7］相比于传统的相干检测方式而言，避免了信道估计这一难题从而降低了检测算法实现的复杂度，更适用于实际应用环境中.然而也带来了3dB的性能损失，为了缩小这个性能差距，提出了多符号差分检测技术［8-11］.

目前，MSDD算法最常见的有 ML（maximum-likelihood最大似然）、SD（sphere-detection球形译码）［8，9］、ASD（automatic sphere-detection自动球形译码）［10］和 PASD（pruning automatic sphere-detection裁减自动球形译码）［11］.其中，多符号ML算法对每条分支检测的操作造成了系统运行时高复杂度的问题，由此提出了多符号SD算法.SD算法大多是基于树形检测，检测方式多样化，包括深度优先［8］和宽度优先［9］为主的检测方式.同时，在SD算法的基础上提出了ASD算法［10］，减小了系统性能对球形半径的敏感性.然而ASD算法需要建立一个存储列表，并对列表中最小的度量值进行扩展，为了减少ASD算法维护存储列表的压力，提出了PASD算法［11］.PASD算法在ASD算法的基础上加入裁减思想，通过设定裁减阈值来实时的裁减掉那些扩展概率较小的节点，减少维护存储列表时节点比较次数，从而降低了系统的平均复杂度.

由此看出，PASD算法达到了算法性能与复杂度之间很好的折中效果.然而在差分协作系统中，大多数是对ML和SD算法的性能以及度量公式推导进行研究［12］，对PASD算法的研究依然尚未涉及，因此本文通过将多符号PASD算法引入差分协作系统中来降低系统实现的复杂度.在文中，首先对应用于差分协作系统中的ML算法和SD算法进行研究分析.然后，针对ML算法高复杂度的缺点和SD算法检测时受球形半径限制的问题，在差分协作系统中提出了PASD算法，并且分析了当协作系统参数变化时对PASD算法性能的影响.

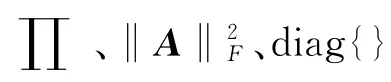
1 系统模型

考虑在AF协作方式下的差分酉空时协作系统，其系统模型如图1所示，其中S、Ri、D分别表示源节点、第i个协作节点、目的节点.考虑在平坦瑞利衰落信道下，无线网络有L＋2个节点，其中一个源节点、一个目的节点和L个协作节点.

图1 差分酉空时协作系统模型Figure 1 System model of differential unitary space-time cooperative

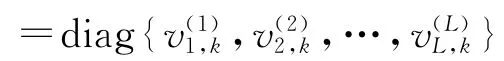
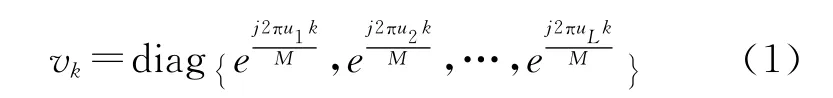
由上述式子可知，vk具有酉特性，即vkvHk＝IL.M＝2LR表示星座点数，可以看出随着协作节点数目的增加，星座点数成指数型增加.然后对酉空时信号进行差分处理（DUSTM）：

进行差分酉空时调制后，协作通信分为两阶段执行.第一阶段：源节点将差分酉空时信号广播至协作节点，其中fi表示源节点至第i个协作节点；第二阶段：协作节点对接收的信号进行放大转发至目的节点，为了便于分析，假设放大倍数G＝1，其中gi表示第i个协作节点至目的节点之间的信道增益.假设在准静态瑞利信道条件下，其元素都是独立同分布的圆对称高斯分布信道增益样值，则gi、fi都服从CN（0，1）.Ψk为高斯白噪声，表示第k个DUSTM符号的噪声样值，服从CN（0，1）.

最后，目的节点对接收的信号进行多符号差分处理.假设多符号差分检测的分组长度为N，则目的节点存储N个接收信号后再进行译码解调处理.此时，接收信号可以表示为：

其中

根据AF协作方式可得：hi＝Ggifi，则Hk＝（h1，h2，…，hL）T，Xk＝（x1，k，x2，k，…，xL，k）T.在多符号差分检测系统中，接收机接收N个符号来检测出N-1个符号，本文多符号差分检测的判决度量公式采用如下形式［13］：

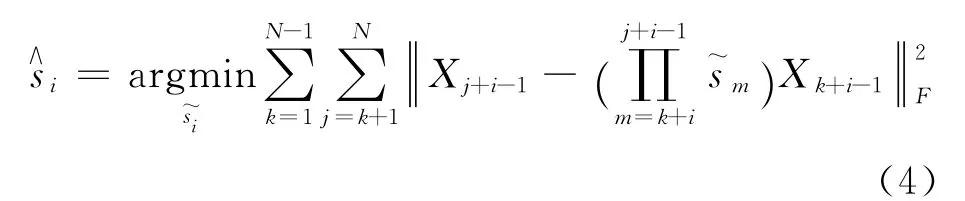
2 多符号差分检测

在协作系统中，随着协作点数的增加，信道数目也相应的成倍增加.如果采用相干检测，则信道估计的工作量也会相应增大；如果采用多符号差分检测技术，不仅避免了信道估计，降低了检测复杂度，而且缩小了单符号差分检测与相干检测之间3dB的性能之差.多符号差分检测算法的种类很多，都可以在树形结构的基础上实现.

其中，ML算法作为最原始的检测算法，对接收信号所有可能的分支度量值进行检测，其算法保证了最优越的误码性能，但是同时扩展所有的分支节点，从而造成了大幅度降低系统的复杂度性能.

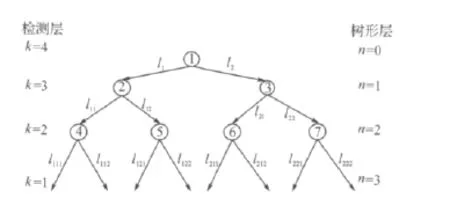
图2 L＝1，N＝4时多符号差分ML检测搜索示意图Figure 2 Multiple-symbol differential ML search schematic diagram when L，Nis 1，4respectively.

为了简化多符号差分ML检测过程，协作节点数目设定为L＝1，此时星座点数M＝21，则每个节点具有两条可能的扩展的分支。同样，随着协作节点个数的增大，星座点数成指数型增长.图2是L＝1，N＝4时多符号差分ML检测示意图，可以看出检测过程中一共需扩展7个节点，其中，表示扩展的第i个节点；每条分支上的li是利用（4）式得到的被扩展节点的判决度量值；n表示为树层，从上到下为0，1，…N-1；k表示为检测层，从上到下为N，N-1，…，1。根据公式（4）可得每条分支的判决度量值计算公式为：（注：lm∈｛l1，l2｝；lmp∈ ｛l11，l12，l21，l22｝；lmpq∈ ｛l111，l112，l211，l212，l221，l222｝；即 m，p，q，i∈｛1，2，…，M｝）

当k＝2时，

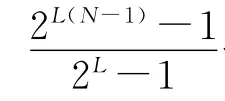
本文通过引用M-SD算法［9］作为比较分析对象，M-SD是一种以宽度优先为主的检测方式，通过设定球形半径后，每层节点的分支度量值与之比较，逐层删减掉大于球形半径的分支节点，直至k＝2时，选取度量值最小的分支作为输出信号.然而SD算法实现的复杂度受球形半径因素限制，在低信噪比区域，复杂度改善不明显.

在传统MIMO系统中提出了一种新型球形算法——PASD 算法［11］，融合了自动和裁减思想，不仅降低了系统的平均复杂度，而且减少了系统复杂度对球形半径设计的敏感度.本文通过引用PASD算法，来达到降低协作系统复杂度的目的.PASD算法首先建立一个存储列表，用于存储扩展节点的判决度量值；然后通过设定一个裁减阈值，实时的删除掉那些被扩展概率很小的节点；最后通过排序，选择路径值最小的节点作为扩展节点，直至k＝2时，选取度量值最小的分支作为输出信号.本文为了保证协作系统的性能，最大似然节点不较早的被删除，n＝1时不进行裁减操作，同时n＝N-1最后一树层也不做裁减操作.

图3 PASD在不同协作节点个数下的误码率比较Figure 3 Comparison of PASD error rate under different number of cooperative nodes

图4是在不同分组长度，L＝3的情况下，PASD算法与 ML、SD算法性能比较图.可以看出即便裁减概率p＝0.99，在系统误码性能不好的情况下，PASD算法相比于ML、SD算法的误码性能损失也很小.当分组长度N＝5、信噪比SNR＝15dB时，PASD、SD算法性能差距最大.

3 系统性能分析

针对ML算法具有高复杂度的不足，以及SD算法的复杂度性能对球形半径的敏感性从而导致系统平均复杂度较高的缺点，在差分酉空时协作系统中提出了多符号PASD算法.为了验证PASD算法的有效性，本文在差分酉空时调制、AF协作方式、准静态瑞利信道、信道频偏fd＝0.007 5Hz并且 PASD 算法的裁减概率值［11］为p＝0.99的仿真环境下，从误码率和复杂度两方面来对PASD算法分析.

图3和图4对PASD、SD、ML三种算法的误码率进行比较分析.

其中，图3显示了协作参数对应用于协作系统中的PASD算法性能的影响，可以看出在信噪比为16左右时，误码率曲线发生变化.假定SNR＝16为信噪比阈值，在小于信噪比阈值的范围内，协作节点个数的增加对误码率性能的提高没有影响，反而降低了系统误码性能；然而当信噪比大于信噪比阈值时，系统的误码性能随着协作节点个数的增加而提高.

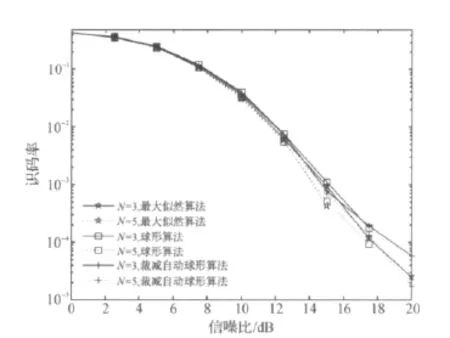
图4 三种算法在N＝3，5时系统误码性能比较Figure 3 Comparison of three algorithms error rate when Nis 3or 5

图5和图6对PASD、SD、ML三种算法的复杂度进行比较分析.本文的复杂度主要是从扩张节点的角度来分析系统多消耗的复杂度.

其中，图5显示了在分组长度为3的情况下，PASD算法在不同协作节点个数下扩展节点数的比较.从图中，可以清晰的看出随着节点数目的增加，系统的复杂度开销也相应增大，然而随着信噪比的增大，他们之间的差距也越来越小.但是，由于协作节点个数的增加，只是增大了星座点数的空间大小，在相同分组长度情况下仿真，树形检测层数保持不变.因此，在高信噪比的情况下，达到理想状态，每层只需扩展一个节点，此时协作节点个数的变化不会影响系统复杂度性能，所有的曲线都最终回归于同一点.

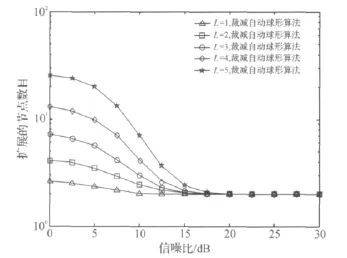
图5 PASD在不同协作节点个数下的复杂度比较Figure 5 Comparison of PASD complexity with different number of cooperative nodes

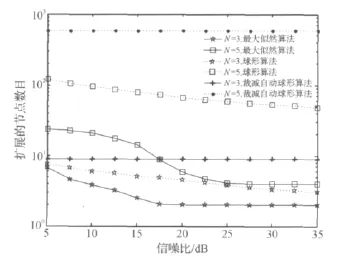
图6 三种算法在不同分组长度下的复杂度比较Figure 6 Comparison of three algorithms error rate with different observe window sizes

图6显示了PASD，SD，ML三种算法在分组长度3和5、L＝3时扩张点数的比较.从图中，可以明显的看出ML算法消耗的复杂度最高，不随着信噪比的增加而改变，并且随着分组长度N的增加，访问点数所增大的幅度也是最大.与 ML相比，SD算法所消耗的复杂度随着信噪比的增加而相应减少，然而复杂度曲线收敛比较缓慢，从而导致了系统的平均复杂度相应增大.同样在分组长度N＝5、信噪比SNR＝15dB的情况下，PASD、SD算法的扩展点数分别为14.138 6、78.950 5，从而相应的降低了系统的复杂度.

综上所述，当SNR＞16dB时，协作节点的增加有利于提高系统的误码性能，然而系统的复杂度性能并没有很大的损失；同时，PASD算法的误码性能相比于SD，ML算法几乎没有损失，然而系统的平均复杂度却得到了很好的改善效果.

4 结 语

通过引用PASD算法来解决差分酉空时协作系统中多符号差分检测算法的高复杂度缺点.同时，在误码性能和扩展节点所消耗的复杂度性能两方面对多符号ML、SD、PASD算法进行比较分析.仿真结果表明，当SNR＞16dB时，随着协作节点数目增加，系统的误码性能也相应的提高，然而对系统复杂度的影响很小；同时，PASD算法在误码性能几乎不变的情况下，复杂度曲线比SD算法收敛迅速，降低了系统的平均复杂度.

［1］FOSCHINI G J，GANS M J.On limits of wireless communications in a fading environment when using multiple antennas［J］.Wireless Personal Communications，1998，6（3）：311-335.

［2］SENDONARIS A，ERKIP E，AAZHANG B.User cooperation diversity-part I：system description ［J］.IEEE Transactions on Communications，2003，51（11）：1927-1938.

［3］SENDONARIS A，ERKIP E，ZHANG B.User cooperation diversity-partⅡ：implementation aspects and performance analysis［J］.IEEE Transactions on Communications，2003，51（11）：1939-1948.

［4］LI W，HANZO L.The amplify-and-forward cooperative uplink using multiple-symbol differential sphere detection［J］.IEEE Signal Processing Society，2009，16（10）：913-916.

［5］SWASDIO W，PIRAK C.A novel alamouti-coded decodeand-forward protocol for cooperative communications［C］／／TENCON 2010-2010IEEE Region 10Conference.Bangkok：King Mongkut's University，2010：2091-2095.

［6］JING Y，JAFAKHNI H.Distributed differential space–time coding for wireless relay networks［J］.IEEE Transactions on Communications，2008，56（7）：1092-1100.

［7］ZHAO Q，LI H.Performance of differential modulation with wireless relays in rayleigh fading channels［J］.IEEE Communications Letters，2005，9（4）：343-345.

［8］LAMPE L，SCHOBER R，PAUL V，et al.Multiple-symbol differential sphere decoding［J］，IEEE Transactions on Communications，2005，53（12）：1981-1985.

［9］XIAO P J，YING G Y，NING J.Multiple-symbol msphere detection based on linear radius for differential unitary space-time modulation systems［J］.International Journal of Digital Content Technology and Its Applications，2011，5（4）：201-208.

［10］KAREN S.Efficient maximum likelihood detection for communication over MIMO channels［D］.Cambridge：University of Cambridge Department of Engineering，2005.

［11］李 颖，魏急波.裁减自动球形译码算法与性能分析［J］.通信学报，2007，28（5）：49-54.

［12］HANZO L，AKHTMAN Y，LI W.MIMO-OFDM for LTE，Wi-Fi and WIMAX［M］.United Kingdom Southampton：IEEE Press，2010：380-418.

［13］TAO C，CHINTHANANDA T.Bound-intersection detection for multiple symbol differential unitary space time modulation［J］.IEEE Transactions on Communications，2005，53（12）：2114-2123.