适用于混合网格的约束最小二乘重构方法

康忠良， 闫超

北京航空航天大学 航空科学与工程学院， 北京 100191

适用于混合网格的约束最小二乘重构方法

康忠良， 闫超*

北京航空航天大学 航空科学与工程学院， 北京 100191

为强化边界条件对计算流体力学(CFD)计算中流场重构过程的影响，基于三维任意多面体混合网格，对一种约束最小二乘法进行了研究。通过对不同边界类型的透明化处理，统一了约束方程组的形式，从而简化了该方法的应用。为了充分吸收消去法和加权法各自求解约束方程组的优点，提出了混合采用两种方法的思路。针对层流平板研究了加权法中加权系数如何取值问题，数值实验表明加权系数取到5基本已经足够大。最后通过亚声速层流平板和跨声速湍流ONERA-M6算例对比了混合法、加权法与原始最小二乘法，计算结果表明：约束最小二乘法相比原始最小二乘法的流场重构更加准确，特别是对边界质量较差网格的计算优势更为突出；混合消去加权法相比单独采用加权法的计算结果也有所改善。

混合网格； 任意多面体； 重构方法； 约束最小二乘法； 消去法； 加权法

在计算流体力学(CFD)的应用中，采用混合网格可以充分利用非结构网格的网格生成优势和类结构网格的计算优势，因此是一种先进有效的方法。混合网格的单元类型可以是常用的四面体、金字塔、三棱柱或六面体，也可以是这些单元之间以及与其他任意多面体的混合。

由于混合网格单元类型的任意性及拓扑的随机性，所以必须采用无序的非结构方式来存储，从而给计算带来了很大困难。在空间离散方面，虽然关于非结构高阶格式的研究已有了一定的进展[1]，但由于计算效率和稳定性等多方面的原因，目前混合网格中广泛使用的仍然是二阶空间离散格式，甚至一般二阶精度都难以保证，其主要困难在于流场重构方面[2]。对于普遍使用的Barth and Jespersen[3]提出的线性重构方法，其中梯度计算是问题的关键[4-6]。

目前常用的梯度计算方法主要有格林-高斯法和最小二乘法。其中格林-高斯法在不同单元类型衔接处的梯度计算误差可能会很大，不太适合于混合网格应用[4]。而最小二乘法对于任意形状网格的梯度计算都能达到一阶精度，可满足线性重构的要求，从而保证空间离散达到二阶精度，因此非常适合于混合网格计算。

本文主要针对一种新型的约束最小二乘法展开研究。Ollivier-Gooch and van Altena[7]首先在二维网格上采用消去法研究了约束最小二乘问题，Haselbacher[8-9]后来基于三维混合网格对比分析了消去法和加权法的优劣，但其算法构造对不同边界类型不具有通用性，且没有给出加权系数的取值影响。为方便于实际应用，本文基于三维任意多面体混合网格对约束最小二乘法做了简化和改进，混合采用加权法和消去法进行求解，并选用有效的算例进行了验证和分析。

1 格心有限体积法

本文算法构造基于任意多面体混合网格单元。算法不考虑具体的网格拓扑，对不同的单元类型统一处理(即对网格是透明的)，因此对任意的封闭网格都是通用的。空间离散采用格心有限体积法，控制体取网格单元，控制面取单元表面，流场变量存储在单元中心。

1.1 控制方程

舍去源项的三维非定常可压缩Navier-Stokes方程组在直角坐标系下的守恒积分形式可表示为

(1)

式中：Ω为控制体；∂Ω为控制面；Q为守恒变矢量；Fc为对流通量；Fv为黏性通量;S为面积。各项的具体描述详见文献[10]。

1.2 数值离散方法

对流通量离散采用Roe[11]格式近似求解Riemann问题。假设控制面IJ的左右单元分别为I和J,则对流通量可表示为

|ARoe|(QR-QL)]

(2)

式中：|ARoe|为Roe平均矩阵；QL和QR分别为控制面的左右状态。如果QL和QR分别取左右单元中心的平均值，则空间离散只有一阶精度，为了达到二阶精度，就需要对其进行重构。

Barth and Jespersen[3]提出的线性重构方法假定解在控制体内呈线性分布，面左右两侧的值可表示为

{

(3)

线性重构方法在规整网格上可以使空间离散达到二阶精度[13]。假如梯度是准确值，该方法在任意网格上都可以准确重构，因此梯度计算是重构过程的关键。

另外，考虑黏性通量的椭圆形特征，对其采用中心格式离散，控制面上的值和梯度根据左右单元求取。时间离散采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式格式[10]。

2 约束最小二乘法

由1.2节可知，梯度计算是线性重构的关键，最小二乘法是目前常用的一种梯度计算方法，且非常适合于混合网格计算，下面将基于原始最小二乘法给出一种新型的约束最小二乘法。

2.1 算法构造

采用最小二乘法计算梯度最早是由Barth[14]提出的，它是基于变量在体心值之间的一阶泰勒级数近似，对于单元I和J，可表示为

(4)

将式(4)应用到单元I的所有模板(一般取其所有邻居单元)，便会得到一个线性方程组：

(5)

式中:Δ(*)IJ=(*)J-(*)I；∂(*)U=∂U/∂(*)；q为模板个数；θ为模板加权系数，一般取为1，也可以根据网格几何量或流场解取值，比如取距离倒数加权可表示为

(6)

为便于表示，式(6)可简写为

Ax=b

(7)

式中：A为q×n维系数矩阵，这里n=3，显然对任意网格均能满足q≥n，于是方程式(5)可采用最小二乘法求解[15]。

针对上述最小二乘法，Mavriplis[6]研究指出：加权系数θ采用距离倒数对于在弯曲壁面拉伸网格中保证计算精度比较重要。但是距离倒数加权的一大弊病在于它会导致计算稳定性变差，因此本文中θ取为1。

实际上，可以认为θ是对各个模板影响梯度程度的一种约束，采用距离倒数加权即是强化距离较近的模板的影响。与此类似，如果选取的模板中包括边界，就考虑采取强化边界条件对流场重构的影响，也就是对每个边界控制面施加约束，保证方程的最小二乘解优先满足边界，该方法称为约束最小二乘法，显然这是一个十分合理的思路。

下面构造约束最小二乘方程。Haselbacher[8-9]将不同边界类型区分对待来构造约束方程，导致了算法实现非常繁琐，不利于该方法的实际应用。考虑到算法对边界条件的透明性，本文在每一迭代步采取将不同边界类型均转化为依赖流场变量来定义(比如对于无滑移壁面，速度均取为0，压力取为首层网格格心值，绝热壁处密度取为首层网格格心值，等温壁处密度根据给定温度和首层网格压力由状态方程求取)，这一处理大大简化了约束最小二乘法的实施。对于式(4)，如果认为UI是未知量，在边界施加线性等式约束，构造的约束方程组可统一表示为

(8)

式中：ΔxF，I1、ΔyF，I1和ΔzF，I1分别为边界面模板rI1的x、y和z分量；前p个方程根据边界模板来确定，求解过程应该精确满足这p个方程；后q个方程根据其他模板来确定，可近似满足。

2.2 方程求解

式(8)可采用消去法或加权法求解。消去法是通过某种方法将前p个方程消去然后求解。比如对于图1，要计算单元0处的梯度，选取模板为a-1-2-3-4，则构造的方程组可写为

(9)

对式(9)采用消去法，可降维变形为

(10)

可见式(10)与式(5)类似(注意各下标的区别)，它可以认为是将重构位置从0移到了a，即优先满足了边界。但是该方法只有当模板中存在一个边界时，才能通过消去降维到类似于式(5)的形式。

加权法是对式(8)前p个方程分别施加一个相对较大的权系数然后求解。同样对于图1，要计算单元1处的梯度，选取模板为b-c-0-2-3，则采用加权法构造的方程组最终可写为

(11)

式中：w为大于1的加权法权系数，在保证系数矩阵不病态的前提下，可对其适当加大来强化边界对梯度计算的贡献。

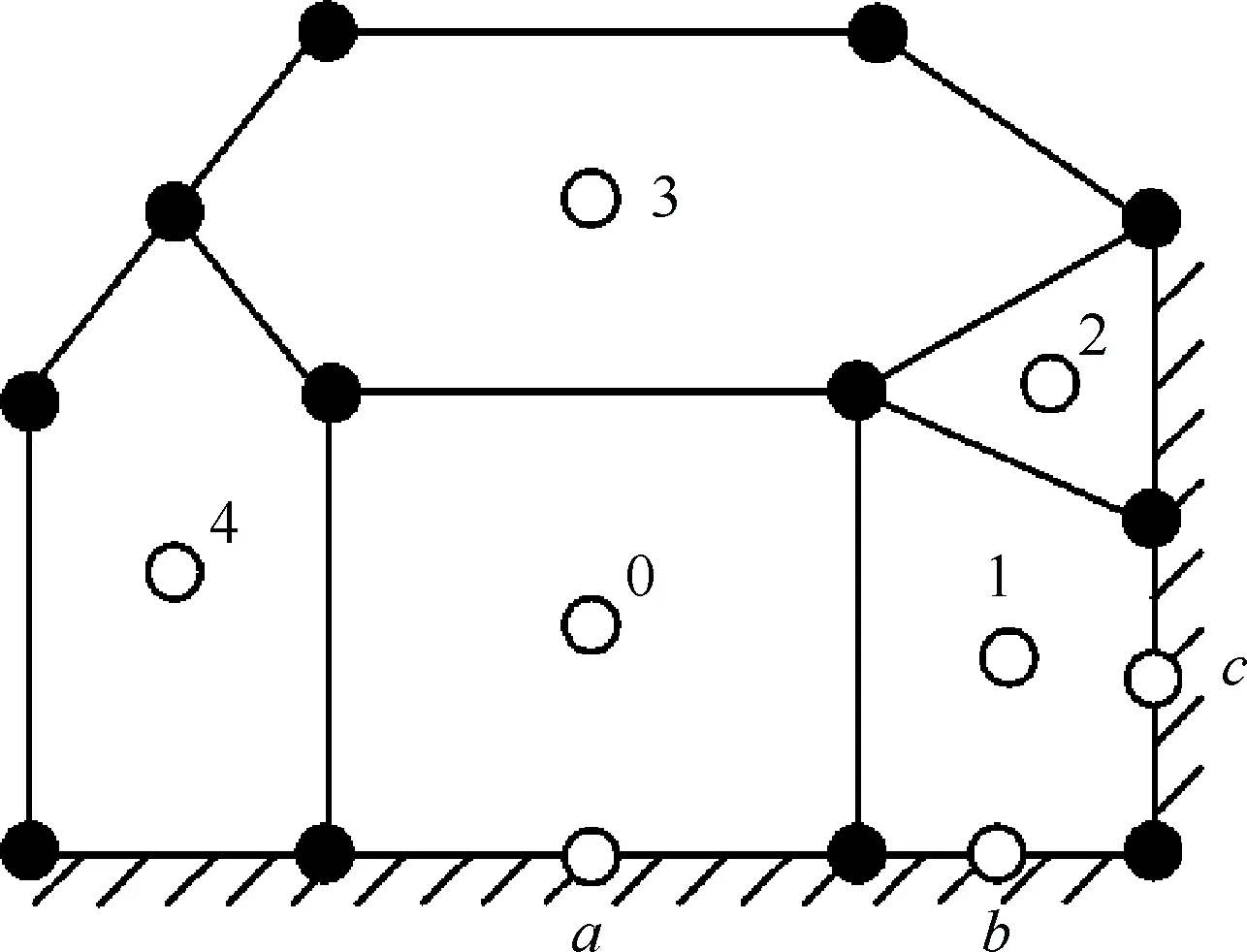
图1 约束最小二乘法构造举例图(a、b和c为边界面)Fig.1 Illustration of constrained least-squares reconstruction (a, b and c indicate boundary faces)

消去法的优点在于可以使约束方程组精确满足边界，缺点是它限制了约束边界个数，且对多个边界的处理繁琐并会导致计算鲁棒性变差；加权法虽然对约束个数没有限制，但其计算的梯度只能近似满足边界，而且加权系数过大又容易导致系数矩阵呈现病态[9]。本文实现中，考虑充分吸收两种方法的优点，采用混合消去和加权法：当模板中只存在一个边界时，采用消去法求解；当存在多个边界时，采用加权法求解。

另外，由于系数矩阵在某些条件下可能会呈现病态，从而导致计算的不稳定，因此本文针对病态情况考虑选取一个优化的模板。具体的模板构造方法为：首先选取计算单元的所有邻居单元组成其初始模板，对于边界曲率较大处及多个边界衔接处附近，适当扩充边界模板；然后判断构造的系数矩阵是否呈病态，病态判断方法详见文献[16]，对于病态模板，利用已选入模板的邻居单元逐层扩大模板，直至系数矩阵转为良态。

3 算例验证及分析

3.1 计算精度验证

因为层流平板存在Blasius精确解，可以严格地测试速度和温度分布的计算精度，因此是验证本文算法的一个很有效算例。

选用3套网格G1、G2和G3，其区别在于边界层内网格数分别取为10、20和40个。计算网格G1如图2所示，板长取一个单位长度，远场取到2倍板长，平板前后均多设置一段对称面用于消除远场的影响。边界层附近采用四边形，以外区域采用三角形，由于程序是三维算法，因此在展向拉伸出一层网格，这样就相当于壁面附近网格单元是六面体，其他区域是三棱柱。

来流马赫数Ma∞=0.3，以板长为特征长度雷诺数Re=1.0×105，壁面取为绝热壁。

图2 平板计算网格G1Fig.2 Computational grid G1 of flat plate

首先基于网格G1，通过数值实验研究加权法中加权系数w的取值问题。暂对所有边界模板的w取相同值，即取w=1，3，5，10，100进行计算。由于摩擦阻力系数Cf的计算主要依赖于壁面处的梯度值和温度分布，因此它对检验约束最小二乘法的计算精度十分有效。图3为采用加权法计算中不同的w值时的摩擦阻力系数的分布，图中x为距平板前缘的距离。从图3可以看出，对于网格G1，加权系数取3左右影响计算结果变化较快，取到5基本已经足够大，再增大到10和100对结果影响不大，因此本文以下计算，加权系数均取为5。

图3 不同加权系数时的摩擦阻力系数分布(网格G1)Fig.3 Skin-friction factor distribution for different weighting coefficients (grid G1)

然后对3套网格分别采用混合消去加权法(Mixed)和加权法(Weighting)，并与原始最小二乘法(Least-squares)进行了对比，如图4所示。

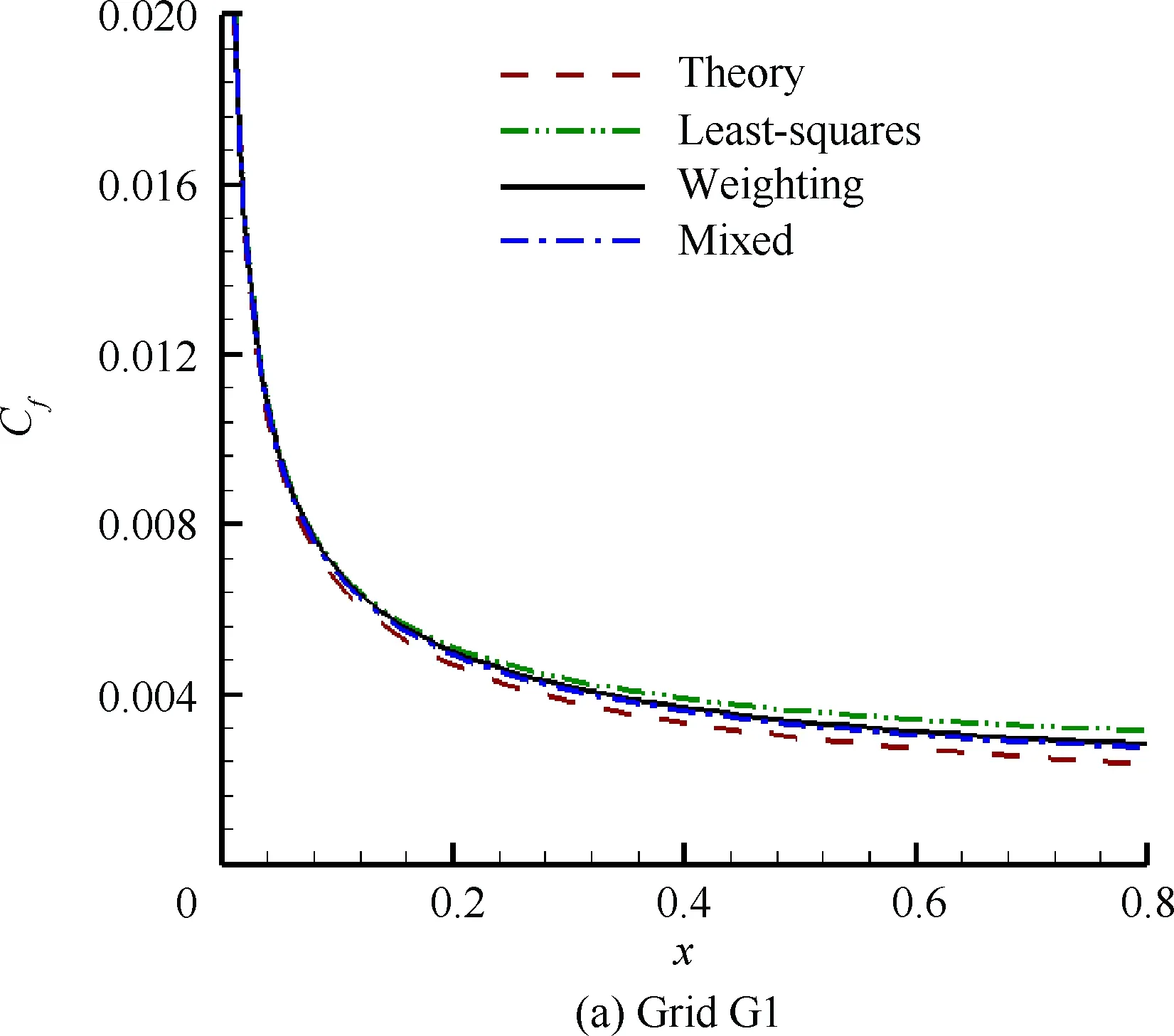
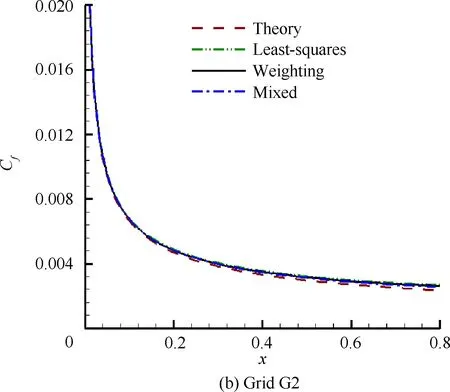
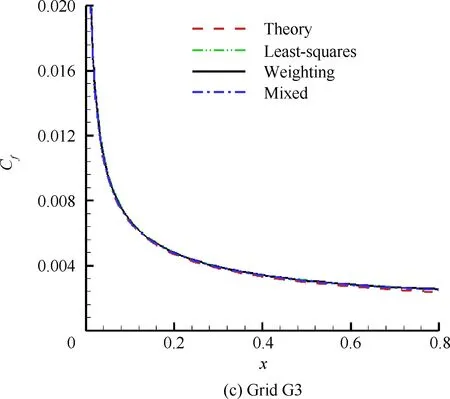
图4 平板摩擦阻力系数分布Fig.4 Skin-friction factor distribution along flat plate

由图4可见，对于较稀疏网格G1，约束最小二乘法相对原始最小二乘法的计算精度提高十分明显，且混合采用消去法和加权法相比单独加权法的精度也有所改善。随着网格的加密，3种方法的计算结果都趋于理论解，约束最小二乘法的优势也变得不太明显，分析主要是因为在边界层特别是线性底层内的网格量足够多时，强化边界影响梯度计算的意义会弱化。也就是说，约束最小二乘法在质量较差网格上的优势更为突出，这对于解决一般混合网格在弯曲壁面附近加密困难的问题十分有效。

3.2 复杂混合网格应用

由于ONERA-M6机翼具有简单的几何外形和复杂的跨声速流动特征，因此是一个经典的CFD验证算例。图5给出了其计算网格，机翼前后缘采用六面体以方便于法向和流向加密，机翼表面其他部分采用三棱柱以方便于法向加密，外围采用四面体填充，四面体与六面体和棱柱之间用金字塔连接。网格总数为187万，第1层网格高度约为机翼平均气动弦长的10-5。Ma∞=0.839 5，迎角α=3.06°，相对于平均气动弦长Re=1.172×107，壁面为绝热壁，湍流模型采用Spalart-Allmaras模型[17]。

图5 ONERA-M6计算网格Fig.5 Computational grid of ONERA-M6

图6给出了采用混合消去加权法的对称面和机翼表面的等密度线r分布，由图可以清晰地看到陡峭的λ激波结构。

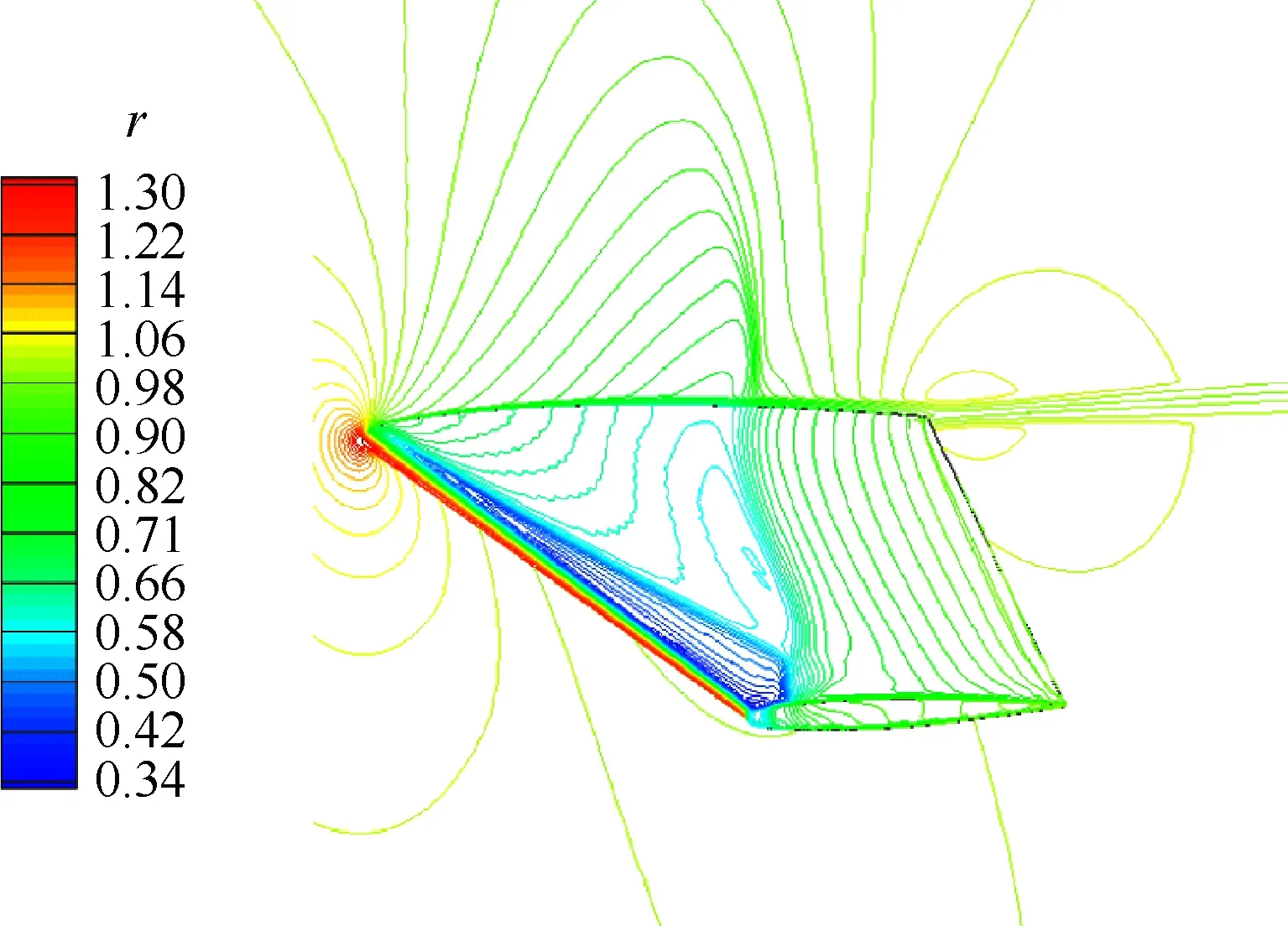
图6 ONERA-M6等密度线(混合消去加权法)Fig.6 ONERA-M6 density contour (mixed method)

图7为ONERA-M6各站位壁面压力系数Cp分布，横坐标x/c为各站位与气动弦长的相对位置。从图7中几个站位的压力分布对比可见，在本算例中壁面附近网格布置较为稀疏的条件下，约束最小二乘法相比原始最小二乘法的计算结果较好，特别是对前缘吸力峰值和激波位置的捕捉更为准确，这主要是因为梯度计算过程强化了边界的影响从而使流场重构更加准确。另外，混合消去加权法较单独加权法的计算结果也更接近于实验值，其差别主要在激波位置附近，原因是混合方法在前缘由于边界模板扩大使加权法生效，发挥了加权法的稳定性优势；在激波位置附近由于模板只包含一个边界使消去法生效，从而发挥了消去法的精度优势。

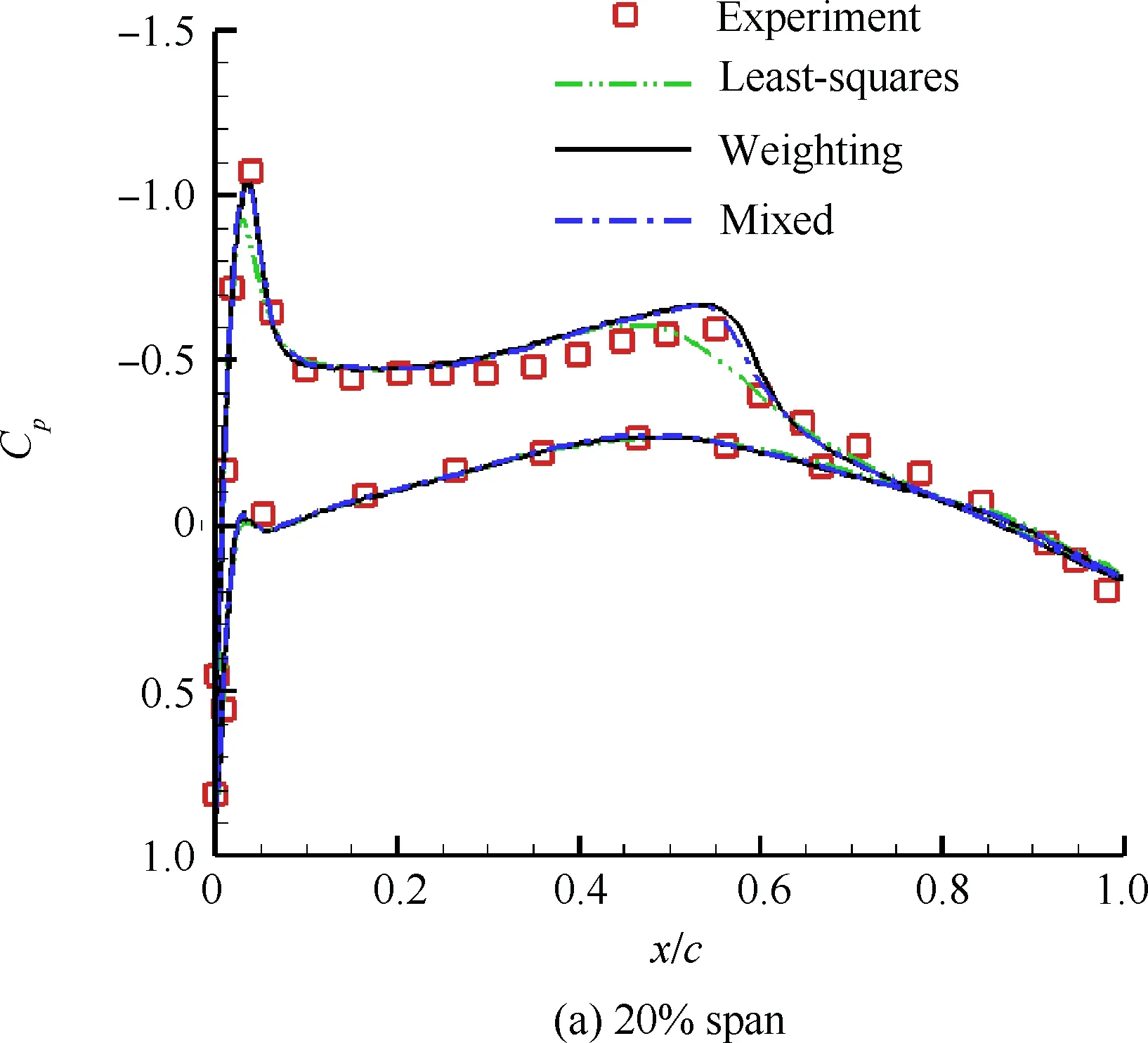
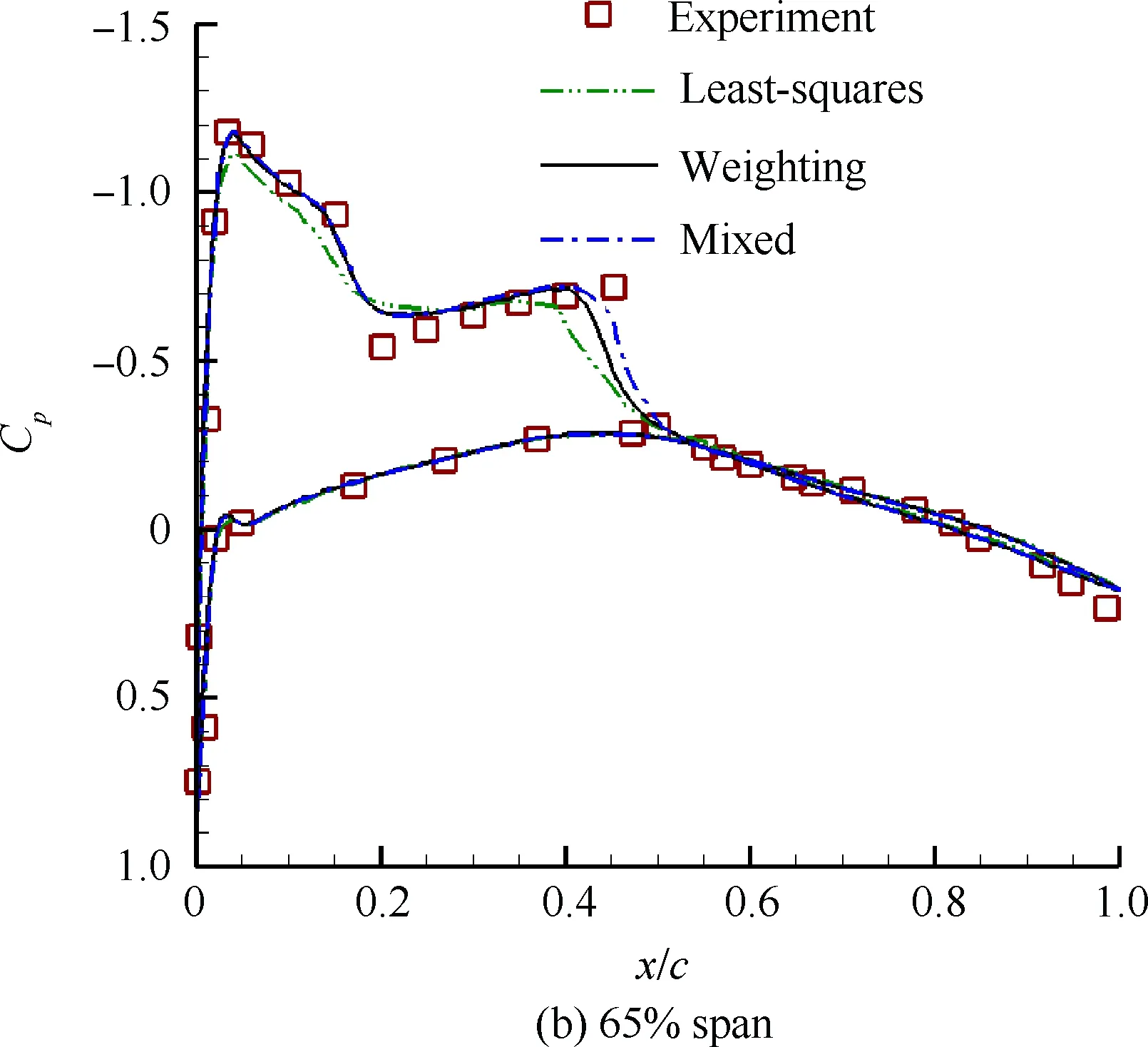
图7 ONERA-M6各站位壁面压力系数分布Fig.7 ONERA-M6 wall pressure coefficient distribution

4 结 论

1) 对不同边界类型的透明化处理统一了约束最小二乘方程组的形式，从而大大简化了该方法的应用。

2) 针对层流平板的数值实验，加权法的加权系数取到5基本已经足够大。

3) 约束最小二乘法强化了边界对梯度计算的影响，相比原始最小二乘法流场重构更加准确，特别对边界质量较差网格的计算优势更为突出。

4) 混合采用消去法和加权法求解约束最小二乘方程，相比单独采用加权法的计算结果有所改善。

[1] Wang Z J. High-order methods for the Euler and Navier-Stokes equations on unstructured grids. Progress in Aerospace Sciences, 2007, 43(1-3): 1-41.

[2] Mavriplis D J. Unstructured-mesh discretizations and solvers for computational aerodynamics. AIAA Journal, 2008, 46(6): 1280-1296.

[3] Barth T J, Jespersen D C. The design and application of upwind schemes on unstructured meshes. AIAA-1989-366, 1989.

[4] Haselbacher A, Blazek J. Accurate and efficient discretization of Navier-Stokes equations on mixed grids. AIAA Journal, 2000, 38(11): 2094-2101.

[5] Smith T M, Barone M F, Bond R B, et al. Comparison of reconstruction techniques for unstructured mesh vertex centered finite volume schemes. AIAA-2007-3958, 2007.

[6] Mavriplis D J. Revisiting the least-squares procedure for gradient reconstruction on unstructured meshes. AIAA-2003-3986， 2003.

[7] Ollivier-Gooch C, van Altena M. A high-order accurate unstructured mesh finite-volume scheme for the advection-diffusion equation. Journal of Computational Physics, 2002, 181(2): 729-752.

[8] Haselbacher A. A WENO reconstruction algorithm for unstructured grids based on explicit stencil construction. AIAA-2005-879, 2005.

[9] Haselbacher A. On constrained reconstruction operators. AIAA-2006-1274， 2006.

[10] Blazek J. Computational fluid dynamics principles and application. Oxford, UK： Elsevier Science Ltd, 2001: 5-25.

[11] Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes. Journal of Computational Physics, 1981, 43: 357-372.

[12] Venkatakrishnan V. On the accuracy of limiters andconvergence to steady state solutions. AIAA-1993-880, 1993.

[13] Aftosmis M, Gaitonde D, Tavares T S. Behavior of linear reconstruction techniques on unstructured meshes. AIAA Journal, 1995, 33(5): 2038-2049.

[14] Barth T J. A 3D upwind Euler solver for unstructured meshes. AIAA-1991-1548, 1991.

[15] Haselbacher A, Vasilyev O V. Commutative discrete filtering on unstructured grids based on least-squares techniques. Journal of Computational Physics, 2003, 187: 197-211.

[16] Zhu Y M, Wang Z Z. A new method for estimate ill-conditioning matrix. Journal of Shanghai Jiaotong University, 1992, 26(3): 110-112. (in Chinese)

朱扬明, 王志中. 病态矩阵判别的一种新方法. 上海交通大学学报, 1992, 26(3): 110-112.

[17] Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows. AlAA-1992-439, 1992.

ConstrainedLeast-squaresReconstructionMethodforMixedGrids

KANGZhongliang,YANChao*

SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100191,China

Inordertoenforcetheeffectofboundaryconditionsonthesolutionreconstructionofcomputationalfluiddynamics(CFD)simulation,aconstrainedleast-squaresmethodbasedonarbitrarypolyhedralmixedgridsisinvestigated.Tomakethemethodsimpler,auniformconstrainedsystemisconstructedthroughtreatingdifferentboundaryconditionsinthesameway.Tomakeuseoftheadvantagesofboththeeliminationapproachandtheweightingapproach,amixedmethodisprovidedtosolvetheconstrainedsystem.Thenumericalexperimentsbasedonlaminarplatesshowthatsettingtheweightingcoefficientto5islargeenoughintheweightingapproach.ThenumericalresultsofasubsoniclaminarflowoveraplateandatransonicturbulentflowoverONERA-M6demonstratethattheconstrainedleast-squaresmethodismoreaccuratethantheoriginalleast-squaresmethod,especiallywhenbadqualitygridsareusedneartheboundary,andthatthemixedmethodshowsimprovedresultsascomparedwiththeweightingapproach.

mixedgrid;arbitarypolyhedral;reconstructionmethod;constrainedleast-squaresmethod;elimination;wei-

ghting

2011-10-23；Revised2011-12-22；Accepted2012-02-01；Publishedonline2012-02-291037

URL：www.cnki.net/kcms/detail/11.1929.V.20120229.1037.007.html

NationalBasicResearchProgramofChina(2009CB724104)

.Tel.：010-82317019E-mailchyan@vip.sina.com

2011-10-23;退修日期2011-12-22;录用日期2012-02-01; < class="emphasis_bold">网络出版时间

时间：2012-02-291037

www.cnki.net/kcms/detail/11.1929.V.20120229.1037.007.html

国家“973”计划(2009CB724104)

.Tel.：010-82317019E-mailchyan@vip.sina.com

KangZL,YanC.Constrainedleast-squaresreconstructionmethodformixedgrids.ActaAeronauticaetAstronauticaSinica,2012,33(9):1598-1605. 康忠良，闫超．适用于混合网格的约束最小二乘重构方法．航空学报,2012,33(9):1598-1605.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

1000-6893(2012)09-1598-08

V211.3

A

康忠良男， 博士研究生。主要研究方向： 混合网格法、动网格法和大型CFD软件平台的研究及应用。

Tel: 010-82318071

E-mail: KZL929@163.com

闫超男， 博士， 教授， 博士生导师。主要研究方向： 计算流体力学和高超声速空气动力学。

Tel: 010-82317019

E-mail: chyan@vip.sina.com