飞虫粘附翼型对翼型气动特性影响的实验研究
2012-11-15肖春生焦予秦高永卫
肖春生,焦予秦,高永卫
(西北工业大学 翼型叶栅空气动力学国家重点实验室,西安 710072)
0 引 言
由于NF-3风洞为直流风洞,风洞入口直接通外界环境,在夏天实验时风洞内会吸入飞虫,实验时飞虫会粘着在翼型模型表面,此种现象也正好与风力发电机叶片在户外工作条件下情况相似。另外在复杂恶劣坏境中长期工作时风力机叶片发生腐蚀、覆盖灰尘或者冰雪等,所有这些等于改变了翼型表面的粗糙度。由于粗糙度的大小和位置将影响到翼型的升力系数和阻力系数以及升力效率,同时也会影响到翼型的失速迎角[1],因此国内外都开展了表面粗糙度对翼型气动性能影响的实验研究。东北农业大学开展了“附着物对直线翼垂直轴风机性能的影响”[2]的研究;汕头大学对风力机翼型前缘表面粗糙度对气动性能的影响也进行了实验研究[3],并得到了相关的试验结果。但是目前所研究的引起粗糙度的元素主要是冰或者固体颗粒,未将自然界中的飞虫作为元素来研究。
针对实际大气情况下翼型表面会被飞虫粘着的问题,进行了实验探索,选用专门的风力机翼型研究表面粘着飞虫后的气动特性。
1 模型及实验设备
1.1 实验设备
实验在西北工业大学NF-3风洞二元实验段中进行。NF-3风洞为直流闭口试验段风洞,二元试验段宽3m,高1.6m,长8m,风速范围20~130m/s,紊流度为0.045%。实验模型(图1)展长为1.6m,弦长为0.8m,剖面为相对厚度35%的翼型。
为了研究模型表面飞虫的分布,将翼型表面共分为3个区(如图1),第二区的上下边界距模型展向中心线为200mm,总高400mm。第一区在第二区上方,高度400mm,第三区在第二区下方,高度为400mm。3个区域的宽度都为400mm,并以翼型前缘为对称上下翼面各有200mm的宽度。每个区域的面积相等且为S=0.4m×0.4m=0.16m2,3个区域的总面积为0.48m2。

图1 实验模型Fig.1 Testing model
1.2 数据采集系统
数据采集系统采用美国PSI公司的9816电子扫描阀,共有683个压力测量通道,采集速度为100Hz/ch,采集精度为±0.05%FS。该系统用来采集翼型的表面压力和尾耙的压力。
1.3 实验方法
采用实验模型竖跨试验段上下壁的方法进行,在模型翼展中心处沿翼型上下表面开静压孔,测量翼型表面的压力,用以计算翼型的升力和俯仰力矩;在模型后缘1.3倍弦长处安装总压排管,测量模型尾迹区的总压分布和静压,用以计算翼型的阻力。
实验内容如下:
(1)Re=1.0×106时,实验前擦拭模型和不擦拭模型(在进行一次Re=4.0×106状态实验后)的对比实验研究;
(2)实验前擦模型,实验起始迎角分别为α=-10°、7°、9°和11°时4个变化过程时的对比实验(Re=4.0×106)研究;
(3)实验前擦模型,α=8°和α=9°时连续实验(Re=4.0×106),每隔1s、30s和5min分别采集一次表面压力分布,研究翼型表面大面积分离的时间和此时翼型表面的飞虫数量。
实验中的飞虫为自然界的普通飞虫,大小约为1.5mm,与翼型模型弦长的比值为0.001875。
2 实验结果与分析
2.1 实验前擦拭模型和不擦拭模型的对比研究
由图2可以看出:Re=1.0×106时,当实验前未擦模型(此时模型上已经粘着有部分飞虫),α<-5°和α>+5°时翼型的升力线斜率明显与实验前擦模型的状态不同,由0.0646变成0.1253,线性度不好;更为明显的是其失速迎角降低了很多,由18°减小到了12°。图3给出了对应的阻力特性对比,实验前未擦拭模型状态在迎角为9°时开始迅速增加,而实验前擦拭模型状态的阻力则是在迎角18°开始快速增加。说明当实验前不擦拭模型时,随着实验的进行模型表面上的飞虫数量持续增加,达到一定程度时引起了翼型上表面大面积的气流分离,从而引起翼型提前失速,并引起阻力相应的快速增加。
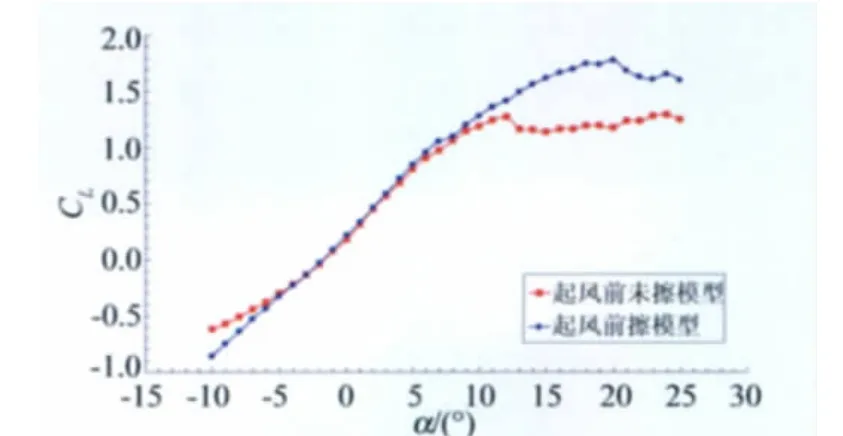
图2 实验前是否擦翼型的升力特性对比,Re=1.0×106Fig.2 Lift characteristics contrast whether the airfoil model wiped or not before testing,Re=1.0×106
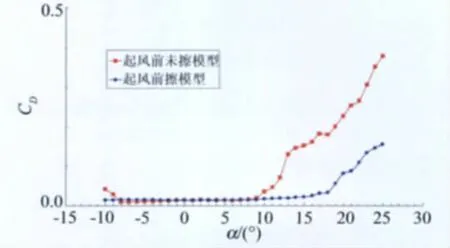
图3 实验前是否擦翼型的阻力特性对比,Re=1.0×106Fig.3 Drag characteristics contrast whether the airfoil model wiped or not before testing,Re=1.0×106
2.2 实验开始迎角分别为-10°、7°、9°、和11°的对比研究
考虑到实验过程中,模型表面粘着的飞虫是随时间逐渐增加的,因此专门研究了雷诺数为4.0×106时,实验前将模型擦干净,选择不同迎角序列的对比试验(起始迎角分别为:-10°、7°、9°和11°),图4和5中给出相应的对比结果。
由图看出迎角从-10°开始实验时,翼型在迎角8°时失速;迎角从7°开始实验时,翼型在迎角9°时失速;迎角从9°开始实验时,翼型在迎角11°时失速;迎角从11°开始实验时,翼型已处于失速状态。对应的阻力特性曲线也呈现类似的规律。通过以上现象来分析,翼型的真实失速迎角是11°,但是在实际实验时随着时间的增加,模型表面粘着的飞虫会大量增加,当达到某个临界状态时将会引起翼型失速,但是这个失速迎角(以下称为表象失速迎角)并不是真实的失速迎角,从本次实验结果来看,真实失速迎角与表象失速迎角之间有着非常大的差别(本研究有3°的差别)。针对风力机翼型而言,由于翼型要在复杂且恶劣的环境下工作,若翼型表面粘着了杂质、飞虫等,将大大降低翼型的气动性能。
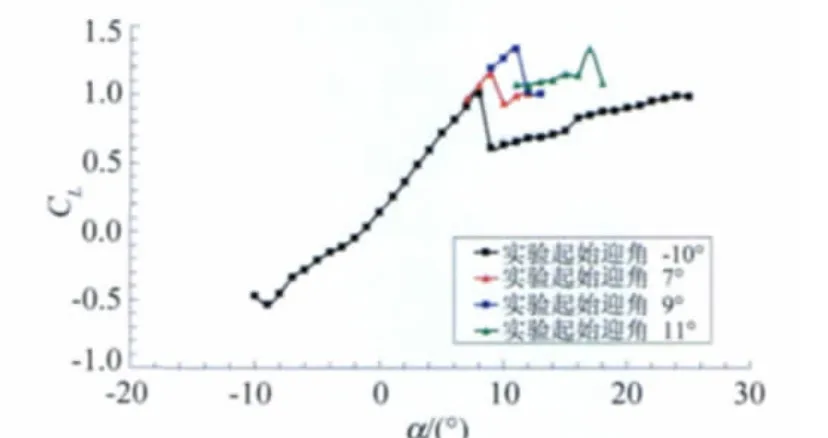
图4 不同迎角序列状态下的升力特性对比,Re=1.0×106Fig.4 Lift characteristics contrast with different beginning angle,Re=1.0×106
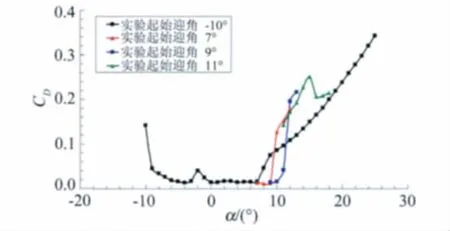
图5 不同迎角序列状态下的阻力特性对比,Re=1.0×106Fig.5 Drag characteristics contrast with different beginning angle,Re=1.0×106
2.3 表面飞虫数量的实验研究
首先在雷诺数为4.0×106,迎角为8°时,进行不同时间间隔周期采集压力分布的对比实验,时间间隔周期为1s、30s和5min。图6为1s间隔周期采集的模型表面压力分布曲线,可见当风速稳定后,83s之前压力分布没有发生变化并且没有明显分离区域,84s时翼型上表面距前缘60%弦长的位置发生了分离,1s后也就是85s时分离位置前移到50%弦长左右的位置,表明在从83~85s的2s内,模型表面粘着的飞虫已经彻底改变了模型表面的流动状态,而此后压力分布则保持不变。分析认为可能由于飞虫在翼型表面的粘着,改变了翼型前缘的流动状态或者是相当于改变了翼型前缘的形状引起了以上的突然变化。从停风后观察,此时1区大致有15只飞虫,2区有59只左右,3区有114只左右;按单位面积算,1区为375只/m2、2区为1475只/m2、3区为2850只/m2,对于整个观察范围平均为1567只/m2。一只飞虫在模型表面的面积大约为1mm2,1567只飞虫所占据的面积大约为1m2的0.16%。
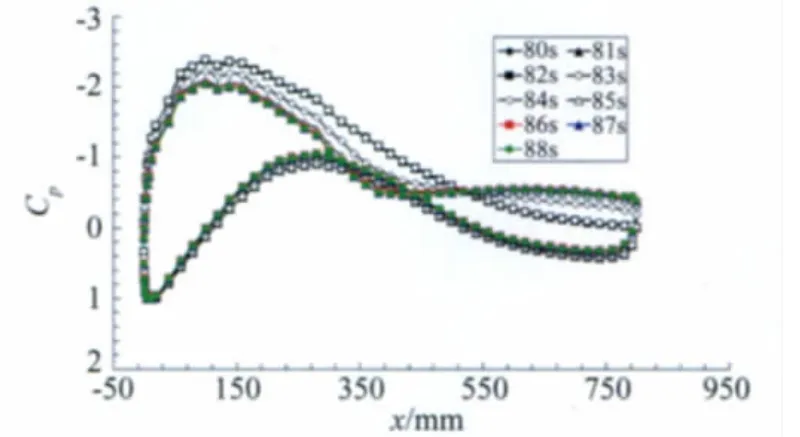
图6 1s周期间隔采集的压力分布曲线,α=8°,Re=4.0×106Fig.6 The pressure distribution curves of 1second periodic intervals acquisition,α=8°,Re=4.0×106
图7为30s周期间隔采集的压力分布曲线,翼型上表面的分离发生在90s的时候,忽略飞虫粘着的不可确定因素以及时间间隔较长的原因,基本可以认为失速发生的时间与间隔1s所得到的失速发生时间相吻合。图8也验证了这个结论,分离是发生在前5min内。由此可以分析认为,当模型从负迎角开始实验时,表面粘着的飞虫逐渐增加,当累积到一定时间和数量时则会引起模型表面大面积的分离。

表1 Re=4.0×106、α=8°时翼型表面飞虫数量表 单位:只、只/m2Table1 Winged insect quantity on airfoil surface,Re=4.0×106、α=8°

图7 30s周期间隔采集的压力分布曲线,α=8°,Re=4.0×106Fig.7 The pressure distribution curves of 30seconds periodic intervals acquisition,α=8°,Re=4.0×106

图8 5min周期间隔采集的压力分布曲线,α=8°,Re=4.0×106Fig.8 The pressure distribution curves of 5minutes periodic intervals acquisition,α=8°,Re=4.0×106
图9为雷诺数4.0×106,迎角9°时时间间隔为1s采集的表面压力分布。至于迎角9°的失速时间(139s)比迎角8°的失速时间(83s)晚的原因可能与表面飞虫的数量和分布有关,但由于该实验状态下为连续测量,并没有进行翼型表面飞虫数量及分布的检测。

图9 1s周期间隔采集的压力分布曲线,α=9°,Re=4.0×106Fig.9 The pressure distribution curves of 1second periodic intervals acquisition,α=9°,Re=4.0×106
另外在雷诺数为4.0×106,迎角为8°时,实验前擦净模型,当风速稳定后立即采集表面压力分布数据,随即停风,并记录模型表面飞虫数量的实验。曲线见图10。图中可见第七次采集时翼型模型表面有50%面积的分离区域。停风后模型表面3个区的飞虫数量如表1,翼型表面的飞虫图像示意照片见图11。

图10 表面飞虫数量研究的压力分布曲线,α=8°,Re=4.0×106Fig.10 The pressure distribution curves of winged insect quantity on the surface,α=8°,Re=4.0×106

图11 翼型表面飞虫Fig.11 Winged insects on airfoil surface
由于飞虫数量是在停风后测量出来的,那么前一次测量的飞虫数量实际上为后一次测量开始前模型上已存在的飞虫数量。表中显示第七次采集后的飞虫数量为334只,而第六次采集结束时为308只,两者的飞虫数量差距不是非常大,但是比雷诺数1.0×106时的188只多出很多,单位面积内飞虫所占据的面积也由0.16%增加到0.28%。说明随着雷诺数的增加模型表面粘着的飞虫数量大量增加。
本次实验只研究了模型表面飞虫数量对翼型失速的影响,没有对表面飞虫的厚度影响进行研究。笔者认为当翼型表面的飞虫数量达到一定量时,由于飞虫厚度的增加,原始的翼型已经发展成了一个新的翼型,从而产生了不同的气动特性,但由于无法测量飞虫的厚度,所以还不能从实验上进行验证,但可以考虑通过数值计算模拟的办法进行初步的计算分析。
3 结 论
通过风洞实验研究,可得出以下结论:
(1)模型表面的飞虫数量会改变翼型的失速迎角即表象失速迎角,该迎角与真实失速迎角有较大差别;
(2)模型表面粘着的飞虫数量累计到一定程度时(蚊虫的大小、数量、覆盖的面积以及翼型本身特性的综合因素),将会导致翼型表面50%区域以上的面积发生分离,引起翼型失速。
[1] WALID Chakriun,ISSA AI-Mesri,SAMI AI-Fahad.Effect of surface roughness on the aerodynamic characteristics of a symmetrical airfoil[J].Wind Engineering,2004,28(5):547-564.
[2] 李岩,田川公太郎.叶片附着物对直线翼垂直轴风力机性能的影响[J].动力工程,2009,29(3):292-296.
[3] 包能胜,倪维斗.风力机翼型前缘表面粗糙度对气动性能影响[J].太阳能学报,2008,29(12):1465-1470.
[4] 王铁城.空气动力学实验技术[M].北京:国防工业出版社,1986.4
