横Π型梁在风洞应变天平阻力结构上的应用

2012-11-15史玉杰田正波

实验流体力学 2012年4期

史玉杰，陈竹，田正波

（中国空气动力研究与发展中心，四川绵阳 62100）

0 引言

大飞机和先进战斗机气动力设计中减阻技术的验证、飞机性能指标的评估，均需要对阻力系数进行精确测量。要对阻力系数进行精确测量，必须要求测力天平尤其是其阻力分量具有高的精准度。

杆式风洞天平的阻力分量由于其结构比较特殊，天平各分量载荷作用在其测量梁上面的应力交错分布，而且应变计粘贴困难，粘贴质量难以保证，相对于天平的其它分量，阻力分量的长期稳定性较差，精准度较低。为了保证阻力的长期稳定性，天平在设计阶段除了要考虑粘贴的工艺性，还必须要考虑如何降低天平其它分量载荷作用在阻力测量梁上的应力（应变）；而要提高阻力测量精准度，则需要提高阻力元的灵敏度并降低其他分量对阻力的干扰，受风洞试验中天平工作环境较差的因素制约，天平阻力元的灵敏度无法大幅度提高。因此，只能在保证天平阻力的长期稳定性以及降低天平其他分量对阻力的干扰方面寻求突破。笔者主要介绍了横Π型梁在阻力测量上的优化应用。

1 传统阻力测量梁结构分析

在天平设计中，阻力分量结构除了支撑梁外，还需要布置专用的测量梁。理想情况下，阻力分量测量梁受力变形只对阻力分量载荷敏感，对其他分量载荷不敏感，其他分量的载荷由支撑梁承受，但是实际上支撑梁没有完全承受其他分量的载荷，造成阻力测量梁也承担了部分其他分量的载荷，产生了相应的应力（应变）。如果天平载荷大，刚度相对较弱，天平其他分量在阻力分量测量梁上产生的应力（应变）就比较大，不利于天平阻力分量的长期稳定，部分应变在应变计组成电桥后不能抵消，形成其他分量对阻力分量的较大干扰项，不利于天平阻力分量精准度的提高。

传统的阻力测量梁主要有T型梁、竖直梁、横Π型梁等，见图1。结构形式多种多样，主要布置在天平元件的中间部位，其作用都是尽可能地保证阻力测量梁对阻力分量敏感的同时，降低对其他分量的敏感性。以阻力和升力作用载荷为例，笔者对传统的T型梁和横Π型梁进行了分析，结果如下：

图1 常见阻力测量梁Fig.1 Familiar measurement beam of axial force

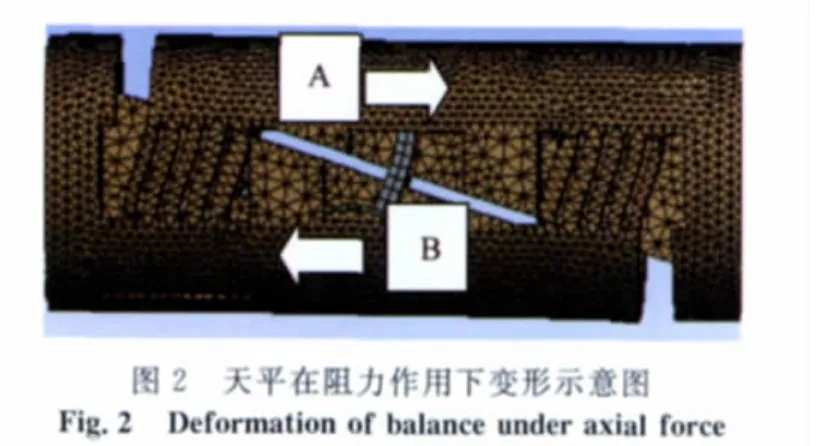
对于T型梁，在阻力载荷作用下，天平阻力支撑梁相连的A、B两部分产生轴线方向的相对位移（图2），阻力测量梁也产生相应变形，形成阻力分量的应变输出；在升力载荷作用下，A、B两部分主要在升力方向产生相对位移，该位移基本上可以被阻力测量梁上布置的铰链等结构消除，对阻力测量梁影响不大，但是由于A、B两部分刚性分布不均匀，造成了这两部分在升力方向产生相对位移的同时，在轴线方向也有相对位移，该位移同阻力载荷作用下位移方向一致（图3），粘贴在T型梁根部的电阻应变计组成阻力电桥后无法抵消其应变输出，从而形成了升力对阻力的干扰，且升力载荷越大，该干扰量也愈大。所以，对于竖直梁以及由此衍生的布置有各种铰链结构的以竖直结构为主的测量梁，由于刚度分布不均匀造成的升力对阻力的干扰均无法通过电桥组合来消除。

对于横Π型阻力测量梁，A、B两部分在轴线方向产生位移时，其变形为纯弯曲变形（图4），应变计可以粘贴在任意位置而阻力的应变输出不变，如果是在法向产生位移，则测量梁变形为对称的S型变形（图5），所以，在升力载荷的作用下，阻力测量梁的变形其实是轴线纯弯曲变形与法向对称S型变形的叠加，是不对称的S型变形（图6）。在传统应变计粘贴工艺中，阻力分量的电阻应变计都是对称粘贴在横Π型梁的中间区域，但是由于在升力载荷作用下，测量梁是非对称的S变形，对称的应变计粘贴区域的平均应变是非对称的，且与阻力载荷作用下产生的应变方向一致，无法通过电桥抵消，同样造成了升力对阻力的干扰。

根据上述情况可知：以T型梁为代表的布置有各种铰链结构的竖直型测量梁以及传统的横Π型梁测量方式都不能降低升力对阻力的干扰，但是对于横Π型阻力测量梁，因为应变计粘贴位置的任意性以及在升力载荷作用下的S型变形，如果对其进行优化并对应变计粘贴位置进行控制，则有可能降低升力对阻力的干扰。

2 横Π型梁优化改进

众所周知，在阻力载荷作用下横Π型阻力测量梁的变形为纯弯曲变形，所以将应变计粘贴在测量梁的任何位置都对阻力的灵敏度无影响，而在升力载荷作用下，横Π型阻力测量梁的变形为非对称的S变形，S变形的中间部位是正负应变的过渡区域，应变值很小且其平均应变接近于零。综合分析阻力载荷和升力载荷作用下横Π型阻力测量梁的变形情况，可以将应变计粘贴在S变形的过渡区域，这样在保证阻力灵敏度不变的情况下可以有效降低升力对阻力的干扰。为了方便描述，下文提到的应变计粘贴部位都是指在升力载荷作用下横Π型梁S变形的中间过渡区域，图7为天平元件在升力载荷作用下A、B两部分在轴线方向的相对位移有限元分析示例图。从图7可以看出，当横Π型测量梁之间跨度越大时，轴线方向的相对位移也越大。由于传统的横Π型测量梁跨度较大，且测量梁轴线方向的长度较短，造成的结果一是应变计粘贴部位由于测量梁的长度尺寸有限从而使其靠近测量梁的端部，而天平各分量作用在测量梁端部的应力较大；二是天平各分量作用在其上面的应变较大，应变梯度也很大，不利于电阻应变计的长期稳定性。

针对传统横Π型梁测量方式存在的问题，笔者提出了优化方式：降低横Π型梁的跨度，加长其轴线方向的长度，并根据有限元分析结果将电阻应变计布置在升力载荷作用下横Π型梁S变形的中间过渡区域，结构形式见图8。由于测量梁跨度较小，其轴线方向的相对位移较小，应变计粘贴部位偏离测量梁中心较小，而且由于测量梁的长度较长，使得上面的应变梯度明显改善，有效降低天平其余各分量作用在应变计粘贴部位的应力，该改进方式将大大降低升力对阻力的干扰，并有利于提高电阻应变计的长期稳定性。

3 改进型横Π型梁在天平上的应用

图10 X测量梁应变计粘贴位置Fig.10 Position of strain gauge bonding on X－measurement beam

针对某型飞机高速风洞试验测力天平的设计载荷大、模型空间限制严的要求，笔者研制了3N6－47A天平（图9），天平设计载荷见表1，该天平的阻力分量采用了改进型的横Π型测量梁结构，并根据有限元分析结果，将电阻应变计非对称地布置在阻力测量梁上（图10）。阻力分量组桥后受到的干扰应变见表2，可以看出，应变计组成电桥后，各分量对X分量的干扰较小，达到了设计预期。3N6－47A天平在中国空气动力研究与发展中心BCL－20000校准架上进行了静态校准，校准过程中天平回零良好，性能稳定，校准结果与分析结果对比见表3，静态校准结果表明：天平实际校准结果与理论分析吻合。