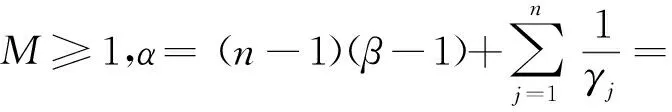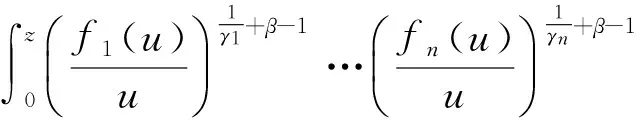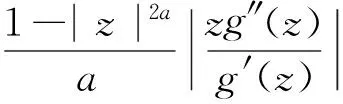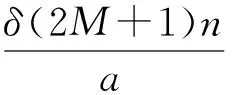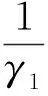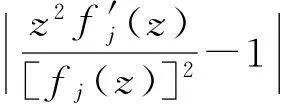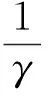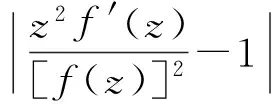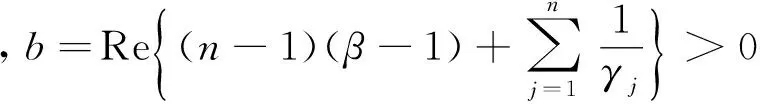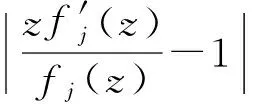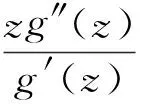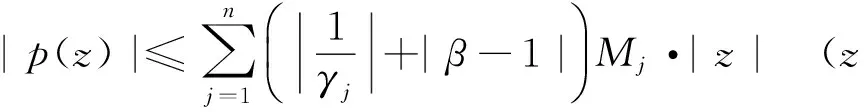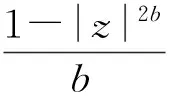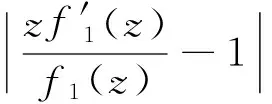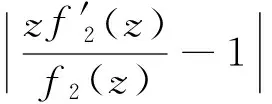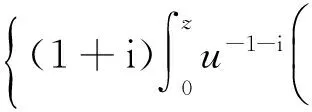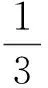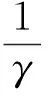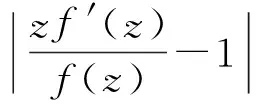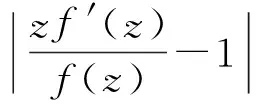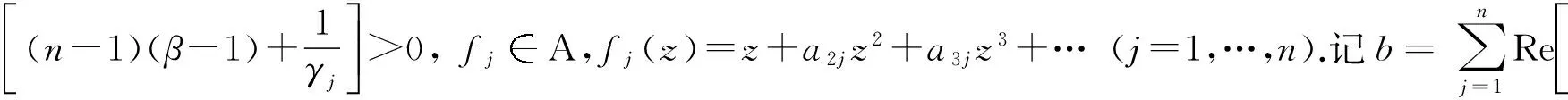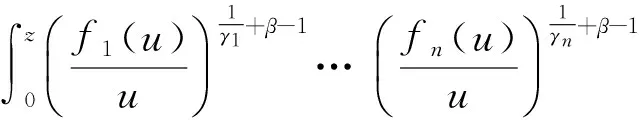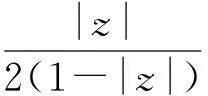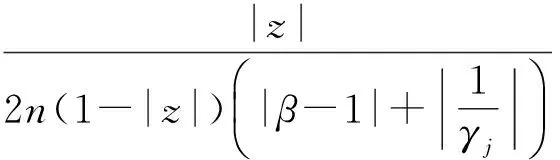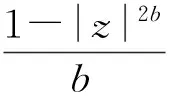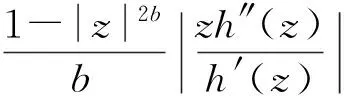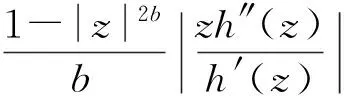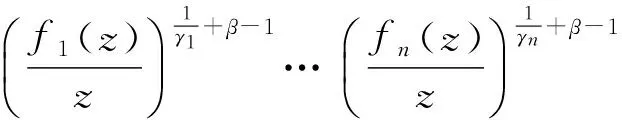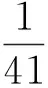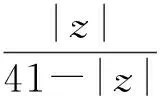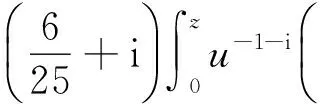一个积分算子的单叶性
2012-11-14刘名生
许 燕,刘名生
(华南师范大学数学科学学院,广东广州 510631)
一个积分算子的单叶性
许 燕,刘名生*
(华南师范大学数学科学学院,广东广州 510631)
引入了一个定义在单位圆={z:|z|<1}内规范化的解析函数类A上的积分算子Jγ1,…,γn,β(z),利用著名的Becker单叶性判别法、Schwarz引理和Caratheodory不等式,得到了这个积分算子在单位圆内单叶的3个充分条件.即当fj(z)(j=1,2,…,n)及参数γ1,…,γn,β满足一定条件时,积分算子Jγ1,…,γn,β(z)在单位圆内是单叶的.
解析函数; 积分算子; 单叶性; 星象性
令A表示形如
文献[3]研究了以下积分算子:

(1)
并得到了积分算子Jγ1,γ2,…,γn(z)在单位圆内单叶的一些充分条件.
文献[4]引入了积分算子:
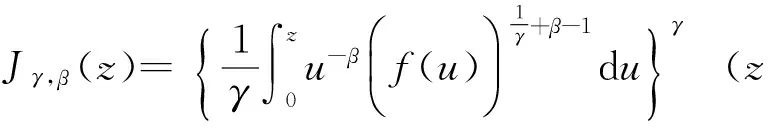
(2)
本文的目的在于推广以上积分算子, 为此引入如下更一般的积分算子:
(3)


(4)
1 引理
为了导出本文的主要结果,需要如下引理.

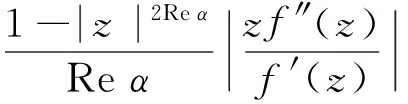
则积分算子Fα

属于S.
引理2[7]设f(z)是在圆盘R={z;|z| 等号(不等式中z≠0)成立当且仅当 这里θ是一个常数. 引理3[8-9]设f(z)是在内的解析函数, 且f(0)=0. 若对某个固定的M>0,f(z)满足 Ref(z)≤M, 则 则由式(1)定义的积分算子Jγ1,γ2,…,γn,β(z)属于S. 证明我们观察得 (5) (6) 于是 (7) 且 (8) 所以 现在由定理1的假设, 有 再根据Schwarz引理, 得 (9) 因此,由式(9)和定理1的假设, 可得 根据引理1,可得式(1)的函数Jγ1,γ2,…,γn,β属于S.证毕. 属于S. 如果在定理1中令n=1, 可以得到下面这个有趣的结果. (10) 且 (11) 则式(1)的积分算子Jγ1,γ2,…,γn,β属于S. 证明观察得Jγ1,γ2,…,γn,β(z)为式(5)的形式. (12) 则有p(0)=0,由式(8)和式(12)得到 (13) 应用引理 2 可得 (14) (15) 因为 (16) (17) 根据式(7)和式(17), 应用引理 1 可以得到式(1)的积分算子Jγ1,γ2,…,γn,β属于S,定理得证. 且满足 所以由定理2,可以得到 属于S. 注记1 在定理2中令n=1, 可以得到文献[3]的定理3.5;在定理2中令β=1,可以得到一个改进了文献[4]的定理3.1的结果. f(z)=z+a21z2+a31z3+…. 若 则积分算子Jγ,β属于S. 证明在定理2中取n=1,f1=f,γ1=γ,b=Re(1/γ), 即可得到推论2. (18) 或 (19) 证明令 (20) 函数h(z)在内正则, 有 (21) 定义函数 可得到ψj(0)=0 (j=1,…,n). (22) (23) 由式(21)和式(22)可得到 (24) (25) (26) 由式(20)有 再由式(25)、(26), 应用引理 1 可得到式(1)的积分算子Jγ1,γ2,…,γn,β属于S, 定理得证. 且满足 同理可得 所以由定理3,可得 属于S. 且满足 同理可得 所以由定理3,可得 属于S. 注记2 在定理 3中, 如果令β=1, 即可得到文献[4]的定理3.4;若令n=1, 可得到文献[3]的定理3.1. [1] 刘志文,刘名生.某类解析函数子类的性质与特征[J].华南师范大学学报:自然科学版, 2010(3):11-14. [2] 李宗涛, 刘名生. 一类解析函数的系数泛函[J].华南师范大学学报:自然科学版, 2005(3):86-91. [3] PESCAR Virgil, BREAZ Daniel. On an integral operator[J]. Applied Mathematics Letters, 2010,23:625-629. [4] PESCAR Virgil. On the univalence of an integral operator[J]. Applied Mathematics Letters, 2010,23:615-619. [5] KIM Y J,MERKES E P. On an integral of powers of a spirallike function[J]. Kyungpook Math J, 1972,12:249-253. [6] PASCU N N. On a univalence criterion, itinerant seminar functional equations, approximation and convexity[M]. Preprint, Cluj Napoca: Babes-Bolyai University, 1985:153-154. [7] MAYER O. Function theory of one complex variable[M].Bucuresti: Academy Press, 1981. [8] BLEZU D. On univalence criteria[J]. General Mathematics,2006,14(1):87-93. [9] MOLDOVEANU S,PASCU N N,PASCU R N. On the univalence of an integral operator[J]. Mathematica, 2001,43:113-116. Keywords: analytic function; integral operator; univalence; starlike property OntheUnivalenceofanIntegralOperator XU Yan, LIU Mingsheng* (School of Mathematics, South China Normal University, Guangzhou 510631,China) A general integral operatorJγ1,…,γn,β(z) is introduced, which is defined on the class A of normalized analytic functions in={z:|z|<1}. Three sufficient conditions for the univalence of this integral operator in the unit diskare provided by applying the well-known Becker univalence criteria, Schwarz lemma and Caratheodory inequality. That is, the integral operatorJγ1,…,γn,β(z) is univalent in the unit diskwhen the functionsfj(z)(j=1,2,…,n) and the parametersγ1,…,γn,βsatisfy some conditions. 2010-06-04 教育部高等学校博士学科点专项科研基金项目(20050574002) *通讯作者,liumsh@scnu.edu.cn 1000-5463(2012)01-0019-05 O174.51 A 【责任编辑 庄晓琼】

2 主要结果