历元间相位差分运动学定轨精度影响分析*

范城城 彭碧波 陈润静 张 明

(1)中国科学院测量与地球物理研究所，武汉 430077 2)大地测量与地球动力学国家重点实验室，武汉 430077 3)中国科学院研究生院，北京 100049 4)武汉大学卫星导航定位技术研究中心，武汉430079)

历元间相位差分运动学定轨精度影响分析*

范城城1，2，3)彭碧波1，2)陈润静1，2，3)张 明4)

(1)中国科学院测量与地球物理研究所，武汉 430077 2)大地测量与地球动力学国家重点实验室，武汉 430077 3)中国科学院研究生院，北京 100049 4)武汉大学卫星导航定位技术研究中心，武汉430079)

运用自编的GNSS_LEO_KPP低轨卫星运动学定轨软件，分别解算了GRACE_A和GRACE_B卫星DOY220/2011至DOY226/2011共7天的观测数据，通过与JPL事后精密轨道进行比较，其最终运动学轨道精度为10～20 cm。研究结果表明:初轨质量对最终运动学轨道质量高低具有一定影响，可以采用迭代循环运动学轨道作为先验轨道，当迭代循环次数达到五次左右时，最终的运动学轨道精度可以保持在分米甚至亚厘米级。

GNSS;导航卫星;运动学定轨;低轨卫星;初轨

1 引言

与动力学法相比，LEO运动学定轨方法解算的运动学轨道质量主要取决于星载GNSS观测数据质量的好坏，且不受动力学模型误差的影响，所以稳健有效的数据质量控制是取得高精度轨道的重要保证［1-6］。本文采用的数据质量控制方法对先验轨道的质量有很大依赖，研究先验轨道质量对LEO运动学定轨的影响具有一定的意义。

本文主要基于历元间相位差分运动学定轨原理进行研究。瑞士AIUB(Astronomical Institute，University of Berne)的Bernese软件和UNB(The University of New Brunswick)的DIPOP软件都是采用该模型实现定轨定位，之前瑞士伯尔尼大学H.Bock博士、中国的陈俊平博士、郑作亚博士、韩保民博士已经对该种方法做了很多研究工作［7-12］。根据该原理编制了GNSS_LEO_KPP低轨卫星运动学定轨软件，分别解算了GRACE_A和GRACE_B卫星7天观测数据，采用不同精度先验轨道进行运动学定轨，最后进一步对解算的结果做相关分析工作。

2 星载GNSS低轨卫星运动学定轨原理

图1为星载GNSS低轨卫星运动学定轨软件GNSS_LEO_KPP的数据处理流程图。由图1可以看出，该软件主要包括四个处理模块:

图1 星载GNSS低轨卫星运动学定轨软件GNSS_LEO_ KPP的数据处理流程图Fig.1 Data processing flow chart of kinematic orbit determination ofLEO satellite-borne GNSS software named GNSS_LEO_KPP

1)双频测距码无电离层延迟组合精密单点定位模块。该模块主要用来解算每个历元时刻低轨卫星的绝对位置(精度为米级甚至亚分米级)。

2)历元间相位差分数据处理模块。该模块主要解算历元间低轨卫星的轨道位置差分值(精度为厘米级甚至亚毫米级)。

3)绝对位置与差分轨道加权融合模块。利用该模块将解算的低轨卫星绝对位置和差分位置加权融合得到最终的运动学轨道，轨道精度可以达到分米级甚至亚厘米级。

4)观测数据质量控制模块。该模块是整个软件的核心组成部分，观测数据质量的高低直接影响最终解算的运动学轨道质量。本文主要采用选举多数法与中误差控制法相结合的数据质量控制方法。

选举多数法的原理为:在同一个历元，对于同一个接收机来说，假设已知精密卫星星历、精密卫星钟差以及低轨卫星的先验轨道，则不同GPS卫星观测值中接收机钟差应该相同，且接收机钟差改正精度应在测距码精度之内。假设某个历元观测到ns颗卫星，选举多数法实施具体步骤如下:

1)在该历元中每颗卫星的接收机钟差值γc与其他所有卫星的接收机钟差值γc，求差并计算差值绝对值的平均值:

3)计算其他各颗卫星接收机钟差与参考卫星接收机钟差之差，然后进行粗差剔除判断:

其中a类表示接受的观测值，b类表示含有粗差的观测值。

制约选举多数法效果的主要因素是低轨卫星的先验轨道质量以及拒绝阈β取值的大小。历元间相位差分观测值周跳探测方法类似于测距码观测值粗差探测方法。本文用到的先验轨道包括四种方案类型，分别是:

第一种方案:初始迭代近似轨道，即直接采用未预处理的双频伪距近似解算的几何轨道，精度为米级;

第二种方案:五次迭代循环运动学轨道，即整个软件系统循环解算五次后得到的最终运动学轨道;

第三种方案:十次迭代循环运动学轨道，即整个软件系统循环解算十次后得到的最终运动学轨道;

第四种方案:JPL事后精密轨道，轨道精度为厘米级。

3 先验轨道对运动学定轨影响分析

采用GNSS_LEO_KPP软件解算GRACE卫星运动学轨道，采用的数据为:1)GRACE_A和GRACE_ B卫星观测数据GPS1B(DOY220-226/2011，采样率10秒);2)IGS提供的最终GNSS导航卫星精密轨道(15分钟SP3精密轨道);3)IGS提供的最终GNSS导航卫星精密钟差(30秒间隔精密钟差文件);4)JPL提供的GRACE_A和GRACE_B卫星事后精密轨道(60秒间隔GNV1B精密事后轨道)。

3.1 先验轨道对双频P码伪距单点定位精度影响分析

图2 先验轨道对GRACE_A卫星伪距轨道解算结果影响分析Fig.2 Impact analysis of priori orbits playing on the results of pseudorange orbits of GRACE_A satellite

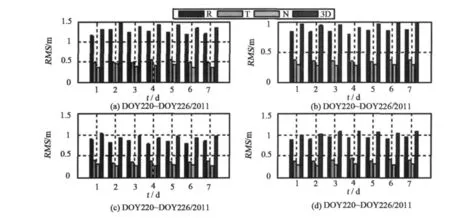
图3 先验轨道对GRACE_B卫星伪距轨道解算结果影响分析Fig.3 Impact analysis of priori orbits playing on the results of pseudorange orbits of GRACE_B satellite

利用GNSS_LEO_KPP软件的测距码伪距数据处理模块解算了GRACE低轨卫星伪距轨道，将解算的伪距轨道与JPL事后精密轨道进行对比分析，对比结果见图2和图3。图2、3之(a)、(b)、(c)、(d)依次对应第一、二、三、四方案。

图2与图3表明:随着迭代循环次数的增加，GRACE_A卫星的伪距轨道精度3D_RMS由原来3～4米提高到1.5米，轨道径向R精度也由原来3～4米提高到1.5米，GRACE_B卫星伪距轨道精度3D_RMS由原来1.5米提高到亚分米级，特别是轨道径向R精度也相应提高到亚分米量级，且A与B卫星在切向T与法向N精度都相应得到改善。GRACE_B卫星的解算结果明显优于A卫星，主要原因可能是GRACE_B卫星观测数据质量与观测几何条件优于A卫星。五次迭代循环轨道作为先验轨道解算的结果接近十次迭代循环的结果，与事后精密轨道作为先验轨道解算的精度相当。主要原因包括:1)测距码伪距本身的测距精度为米级，解算的伪距轨道精度受到本身观测手段制约;2)随着先验轨道精度的逐渐提高，伪距观测值更多粗差被探测和提出，相应伪距轨道精度得到提高。综上所述，先验轨道的精度对伪距轨道精度影响比较大，特别是在轨道R方向，故可以采用迭代循环得到的运动学轨道作为先验轨道，迭代循环次数达到五次左右，伪距轨道精度保持平稳，可以稳定在1米左右，满足本软件的初始设计要求，为GNSS_LEO_KPP软件提供相对较好的绝对位置基准。

3.2 先验轨道对历元间相位差分轨道精度影响分析

利用GNSS_LEO_KPP软件的历元间相位差分数据处理模块解算了GRACE低轨卫星相位伪距差分轨道，将解算的相位伪距差分轨道与JPL事后精密差分轨道进行对比分析。图4与图5类型同于图2与图3。

图4与图5表明:无论是GRACE_A卫星还是B卫星，随着迭代循环次数的增加，解算的历元间差分轨道的精度3D_RMS最终都稳定保持在厘米级甚至亚毫米级，差分轨道径向R精度达到1～2厘米，切向T与法向N精度变化很小，基本保持1厘米左右。迭代循环五次得到的结果与十次迭代结果以及事后精密轨道作为先验轨道解算的结果精度相当。图中还可以看出，先验轨道的精度对于相位伪距差分轨道精度影响不是很大，主要原因是历元间相位伪距差分观测数据精度高，且周跳仅对发生周跳的某历元相位差分轨道精度产生影响，不会对其他历元的差分轨道精度产生影响，故最终的相位伪距差分轨道精度可以稳定保持在厘米级甚至亚毫米级，满足本软件历元间相位差分数据处理模块设计的期望，为GNSS_LEO_KPP软件提供了相当高精度的差分位置虚拟观测值。

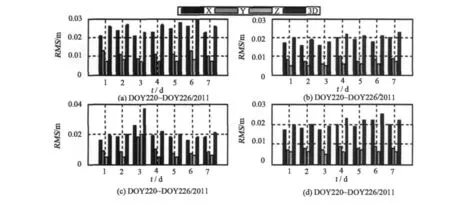
图4 先验轨道对GRACE_A卫星相位伪距差分轨道解算结果影响分析Fig.4 Iimpact analysis of priori orbits playing on the results of differential phase pseudorange orbits of GRACE_A satellite

图5 先验轨道对GRACE_B卫星相位伪距差分轨道解算结果影响分析Fig.5 Impact analysis of priori orbits playing on the results of differential phase pseudorange orbits of GRACE_B satellite

3.3 先验轨道对最终运动学轨道精度影响分析

图6 先验轨道对GRACE_A卫星运动学轨道解算结果影响分析Fig.6 Impact analysis of priori orbits playing on the results of the kinematic orbits of GRACE_A satellite

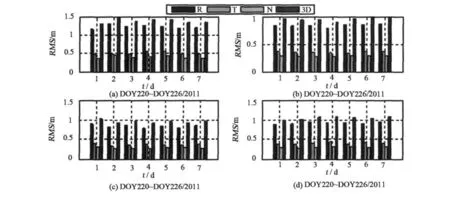
图7 先验轨道对GRACE_B卫星运动学轨道解算结果影响分析Fig.7 Impact analysis of priori orbits playing on the results of the kinematic orbits of GRACE_B satellite

利用GNSS_LEO_KPP软件的绝对位置与差分轨道加权融合模块解算了GRACE低轨卫星运动学轨道，将解算的运动学轨道与JPL事后精密轨道进行对比分析。图6与图7类型同于图2与图3。

图6和图7表明:随着迭代循环次数的增加，相比于JPL事后精密轨道，GRACE_A与B卫星采用五次迭代循环运动学轨道和十次迭代循环运动学轨道作为先验轨道解算的最终运动学轨道精度3D_ RMS可以达到10～20 cm，轨道径向R精度达到10～20 cm，且切向T与法向N精度都得到很大改善，与事后精密轨道作为先验轨道精度相当，达到GNSS _LEO_KPP软件设计的轨道解算的分米级精度期望。图6(c)相比图6(b)，最终运动学轨道精度略有降低，主要原因是过多的迭代循环导致历元间差分轨道变得更加不连续，断裂点处的位置精度取决于伪距轨道精度，故导致整体的运动学轨道精度降低，相应地也对下一次伪距轨道解算和差分轨道解算精度产生影响，分别对比图2(c)和(b)以及图4 (c)和(b)可以得到结论。先验轨道的精度对于GNSS_LEO_KPP软件解算的最终运动学轨道精度影响比较大，主要原因包括:1)当采用的先验轨道质量不是很好时，伪距轨道解算精度不高，故无法提供较好的绝对基准;2)当历元间公共观测卫星数量经数据预处理后不足于解算历元间差分轨道，导致历元间差分轨道断裂，断裂点处的运动学轨道精度取决与伪距轨道精度，故解算的运动学轨道精度不高。综上所述，应当合理地加强伪距观测值质量控制以提高伪距轨道精度，同时适当对载波相位差分观测值质量控制保持宽松，以保证差分轨道历元间的连续性。

4 结论

1)GNSS_LEO_KPP低轨卫星运动学定轨软件解算的运动学轨道精度为分米级甚至亚厘米级。该方法主要原理是将伪距单点位置基准和历元间相位差分位置进行融合，伪距轨道精度对最终运动学轨道精度具有决定性影响，历元间差分轨道的不连续性也会对最终运动学轨道精度产生一定影响。由于伪距单点的位置精度不是很高，无法提供高精度的位置基准，所以最后融合的结果只能保持在分米甚至亚厘米级。

2)为确保最后解算的运动学轨道质量，在无法获得较好质量的动力学平滑轨道时，可以采用迭代循环得到的运动学轨道作为初轨不断的循环解算，且迭代循环次数不宜过多，当迭代循环次数达到五次左右时，解算的最终运动学轨道精度可以稳定在分米级甚至亚厘米级水平。

3)为获得更加高精度的运动学轨道，可以进一步完善观测数据质量控制，整周模糊度的解算与固定进行载波相位精密单点定位，或者与动力学法相结合进行解算。

1 Oliver Montenbruck and Eberhard Gill.Satellite orbits-models，methods，and applications［M］.Germany:Springer， 2000.

2 Heike Bock.Efficient methods for determining precise orbit of low Earth orbiters using the global positioning system［D］.Schwizerland:Astronomical Institute University of Berne，2003.

3 Bock H，et al.Efficient precise orbit determination of LEO satellites using GPS［J］.Advances in Space Research，2002，30(2):295-300.

4 Jäggi A，et al.Precise orbit determination for GRACE using undifferenced of doubly differenced GPS data［J］.Advances in Space Research，2007，(39):1 612-1 619.

5 Van den Ijssel J，Visser P and Patiño Rodriguez E.CHAMP precise orbit determination using GPS data［J］.Advances in Space Research，2003，31(8):1 889-1 895.

6 Li Jiancheng，el al.Precise orbit determination for GRACE with zero-difference kinematic method［J］.Chinese Science Bulletin，2010，55(7):600-606.

7 陈俊平，王解先.基于历元间差分的低轨卫星运动学精密定轨［J］.大地测量与地球动力学，2007，(4):57-61.(Chen Junping and Wang Jiexian.Kinematic precise orbit determination of low Earth orbiter based on epoch-difference strategy［J］.Journal of Geodesy and Geodynamics，2007，(4):57-61)

8 赵齐乐，等.CHAMP卫星cm级精密定轨［J］.武汉大学学报(信息科学版)，2006，31(10):879-882.(Zhao Qile，et al.Precise orbit determination of CHAMP satellite with cm -level accuracy［J］.Geomatics and Information Science of Wuhan University，2006，31(10):879-882)

9 孔巧丽，欧吉坤，柴艳菊.星载GPS相位非差观测粗差和周跳的探测与修复［J］.大地测量与地球动力学，2005，(4):105-109.(Kong Qiaoli，Ou Jikun and Cai Yanju.Detection and repair of gross errors and cycle slips in LEO-based GPS data on zero level［J］.Journal of Geodesy and Geodynamics，2005，(4):105-109)

10 陈俊平.低轨卫星精密定轨研究［D］.同济大学，2007.(Chen Junping.On precise orbit determination of low earth orbiters［D］.Tongji University，2007)

11 李济生.人造卫星精密轨道确定［M］.北京:解放军出版社，1995.(Li Jisheng.Satellite precise orbit determination［M］.Beijing:Liberation Army Publishing House，1995)

12 盛传贞.星载GPS-LEO卫星与GPS导航卫星星座定轨理论与方法研究［D］.中国科学院研究生院，2010.(Sheng Chuangzhen.Studies on the theory and method for precise orbit determination of LEO satellite and GPS navigation constellation［D］.Graduate School of Chinese Academy of Sciences，2010)

ACCURACY IMPACT ANALYSIS OF KINEMATIC ORBIT DETERMINATION BASED ON EPOCH PHASE DIFFERENCE

Fan Chengcheng1，2，3)，Peng Bibo1，2)，Chen Runjing1，2，3)and Zhang Ming4)

(1)Institute of Geodesy and Geophysics，CAS，Wuhan 430077 2)State key Laboratory of Geodesy and Earth’s Dynamic，Wuhan 430077 3)Graduate University of Chinese Academy of Sciences，Beijing 100049 4)GNSS Reseach Center，Wuhan University，Wuhan430079)

The kinematic orbit determination of LEO satellite software named GNSS_LEO_KPP is developed，and the observation data of GRACE_A and GRACE_B satellites in 7 days from DOY220/2011 to DOY226/2011 are calculated.Compared with the JPL precise orbits，the accuracy of final kinematic orbit can reach 10—20 cm.The results show that:the priori orbit quality has a certain level of impact on the final kinematic orbit quality，so we could use the iterative loop kinematic orbit as a prior orbit，and the final kinematic orbit accuracy can be maintained in decimeter or sub-centimeter level.

GNSS;navigation constellation;kinematic orbit determination;LEO;priori orbit

1671-5942(2012)03-0080-06

2012-02-13

国家自然科学基金(41131067，40774012)

范城城，男，1986年生，硕士生，主要研究方向为星载GPS低轨卫星精密定规.E-mail:ccfan@whu.edu.cn

P227

A