L曲线法在等价权抗差岭估计模型中的应用*
2012-11-14高井祥
王 彬 高井祥 刘 超 王 坚 周 锋
(1)中国矿业大学环境与测绘学院,徐州 221116 2)江苏省资源环境信息工程重点实验室,徐州221116)
L曲线法在等价权抗差岭估计模型中的应用*
王 彬1,2)高井祥1)刘 超1,2)王 坚1)周 锋1,2)
(1)中国矿业大学环境与测绘学院,徐州 221116 2)江苏省资源环境信息工程重点实验室,徐州221116)
借鉴相关抗差估计的思想,导出一种基于相关观测的等价权抗差岭估计模型,将L曲线法引入该模型中用于岭参数的求解。针对抗差迭代过程中等价权阵可能不正定而无法使用经典Cholesky分解进行单位化的问题,根据双因子模型的特点,提出一种等价权阵的分解算法对等价权阵进行单位化,使得L曲线法在迭代过程中得以成功运用。算例结果表明:该模型能够有效克服系数阵病态和粗差的影响。
抗差岭估计;L曲线法;岭参数;双因子模型;等价权阵分解
1 引言
在控制网平差、大地测量反演、GPS快速定位等数据处理中存在大量的病态问题,当系数矩阵病态时,经典最小二乘得到的解是极不稳定的,需对系数矩阵的病态性进行处理,一般采用有偏估计的方法,如岭估计,广义岭估计等。另外,由于受到周围环境等因素的影响,观测值可能会受到粗差的污染,即使使用有偏估计,结果可能也不理想,需要引入抗差有偏估计方法。
当前关于抗差有偏估计的研究主要有抗差岭估计[1]、抗差泛岭估计[2]、正则化抗差估计[3]以及针对GPS快速定位的抗差部分岭估计[4]等,这些模型还存在着一些问题,主要是在抗差迭代过程中岭参数或正则化参数的选取,大多对其未作详细探讨或者仍采用最小二乘岭估计所采用的岭参数,少有的一些迭代过程中岭参数选取方法精度也不高且较为繁琐。岭参数的选取对估计结果是至关重要的,由于在抗差迭代过程中,等价权阵可能是不断变化的,所以在理论上需要不断求取相对于每次迭代最合适的岭参数。而如何在算法上实现岭参数的较高精度的自动选取,是抗差岭估计等方法实际运用的关键。
Hansen[5,6]针对不适定问题提出的L曲线法是求解岭参数较好的方法,在最小二乘岭估计中已得到了成功的运用。针对相关观测,本文将L曲线法引入相关抗差岭估计模型中,根据双因子模型的特点,提出一种针对迭代过程中等价权阵可能不正定而无法进行经典乔列斯基(Cholesky)分解的等价权阵分解算法,使得等价权阵得以顺利单位化,从而使L曲线法成功应用于抗差迭代过程中岭参数的求解。最后通过算例,验证了该模型是可靠有效的。
2 等价权抗差岭估计模型
设平差的函数模型为:

式中,ε为相关观测随机误差向量,且E(ε)=0,先验权阵为P,A为n×t阶系数矩阵,X为t维参数向量,对应的误差方程为:

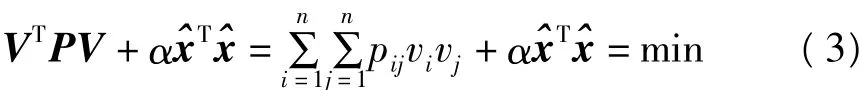

以式(3)作为估计准则得到参数估计,抵抗粗差的能力很弱。借鉴相关抗差估计的思想,用可变函数ρ(vi,vj)代替vivj,这样采取的估计准则为:
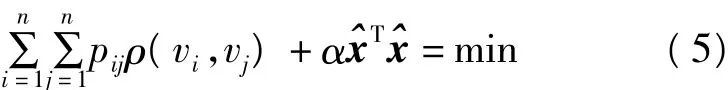
其中ρ为任意选取的函数,Vi=ai-li,式(5)对求导并令导数为零,则:

式中:

由于抗差函数具有对称性[7],式(6)变为:
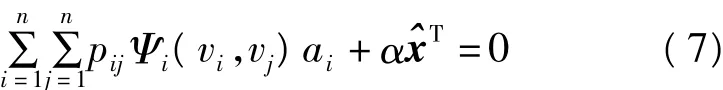
若令Ψj(vi,vj)/vj=wij,则可令=pijwij= pijΨj(vi,vj)/vj
则式(7)可变为:

将式(2)代入式(8)可得:
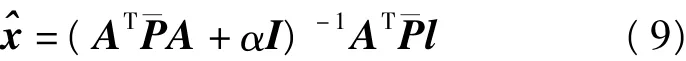
采用杨元喜教授的双因子等价权模型[8],取:
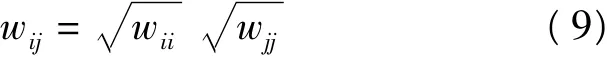
式中wii和wjj为等价权因子,采用IGGⅢ方案计算:


式中,Ngg=A(ATPA+αI)-1AT。
σ0是由中位数计算的单位权中误差,其计算公式为[9]:

式中,k0和k1为阈值,实际计算中,k0取1.5~2.5,k1取2.5~4.0。
3 L曲线法的基本原理及等价权阵分解算法
3.1 L曲线法确定岭参数的基本原理

两边取对数,得:
L曲线上点的曲率的计算公式为[10]:
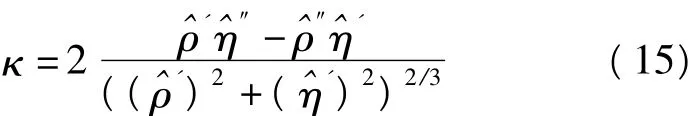
该过程是在权阵为单位阵的前提下推导的,若权阵不是单位阵,需先对其进行单位化[11],一般采用Cholesky分解方法,如对于式(2)的误差方程,其单位化过程为:
对先验权阵P进行Cholesky分解,使P=CTC,C为上三角阵,这样式(4)就变为:
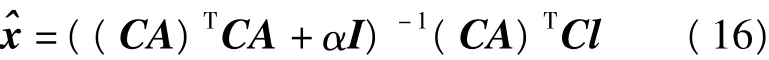
令B=CA,W=Cl,即实现了权阵的单位化,再使用L曲线法即可求解岭参数。
3.2 等价权阵的分解算法
对于最小二乘岭估计,由于先验权阵P一般为对称正定矩阵,可直接使用Cholesky分解进行单位化。在抗差岭估计的迭代中,先验权阵P变为等价权阵且是变化的,因此仍采用最小二乘岭估计所采用的岭参数是不合理的,而需在每次迭代中都使用L曲线法确定合适的岭参数。但是如果观测值中含有明显的粗差,权因子的计算出现了淘汰段,必然会出现全零行和列,为对称不正定矩阵,无法使用经典的Cholesky分解对进行单位化,从而导致L曲线法不能顺利进行。
针对以上问题,本文提出一种等价权阵的分解算法。如果第i个观测值中含有明显的粗差,则在权因子wii的计算过程中,必然会处于淘汰段,使得wii=0,对于双因子模型,则的第i行和第i列必然都为零。根据等价权阵的这种特点,按以下步骤对进行分解:
1)将所有数值为零的权因子在观测值中的序号存入数组ZeroW。设n个观测值中共有m个观测值所对应的权因子为零,则将其序号i1,i2,…,im存入ZeroW。
3)对矩阵G进行Cholesky分解得到上三角矩阵M,使得G=MTM,M∈R(n-m)×(n-m)。
4)在矩阵M中插入m行全零行和m列全零列,且使插入后得到的矩阵的全零行和列的序号对应且与数组ZeroW中的各元素相同。设得到的上三角矩阵为C,C∈Rn×n,则C的第i1,i2,…,im行和列为全零行和全零列。
4 算例分析
本算例是对文献[10]中的算例5.1进行改化而得的,病态设计矩阵为:
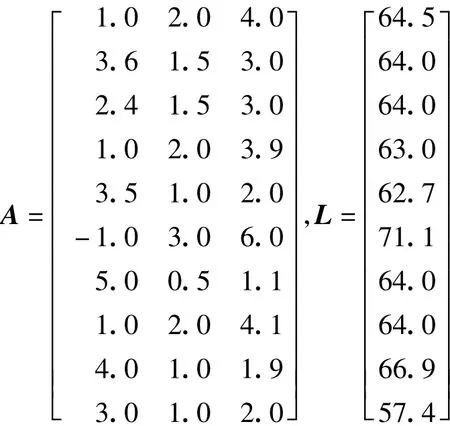
其中A为系数矩阵,L为观测值。未知参数有三个,X=(X1X2X3)T,其真值为X=(10.0 15.0 6.0)T。
将观测值的权阵改化为对角线元素为50,非对角线元素为10的对称方阵,设参数的近似值为X0=(10.5 14.4 5.7)T。求得法方程的条件数cond(ATPA)=6.233 5×104,呈病态。
为分析比较相关抗差岭估计模型的结果,设计以下方案:①不添加任何模拟粗差;②在第二个观测值上加入模拟粗差,且使Δ2=+5.0;③在方案②的基础上,在第十个观测值上加入模拟粗差,且使Δ10=-3.5;④方案③的基础上,在第三个观测值上加入模拟粗差,且使Δ3=+4.5。
分别使用最小二乘估计,最小二乘岭估计和本文基于L曲线法的抗差岭估计模型对方案①~④求解参数,抗差岭估计中取k0=2.0,k1=3.0,迭代收敛精度eps=0.000 1。得到的结果见表1,求得的与真值X差值的二次范数为为后验单位权中误差,m为抗差迭代计算完成后对应权因子为零的观测值个数。
通过对表1计算结果的对比分析,可以得到:
1)方案①中观测值不含粗差,由于受系数矩阵病态的影响,LS估计与真值偏差较为严重,达到3.219 7,方案②~④观测值中粗差的数量从一个增加到三个,由于受到系数矩阵病态和粗差的双重影响,LS估计所得的分别为 15.821 8、18.432 1、16.150 8,参数估值已经完全失真,单位权中误差也明显增大。
2)对于不含粗差的方案①,LS岭估计求得的ΔX仅为0.114 3,可见LS岭估计有效克服了系数矩阵的病态性,而对于方案②~④,由于LS岭估计抵抗粗差的能力很弱,求得的分别为0.963 8、 1.015 8与0.995 7,较LS估计的结果有了明显的改善,但是单位权中误差仍然很大,结果也不是十分理想。
3)对于方案①,由于观测值中不含粗差,所有观测值所对应的权因子均为1,抗差岭估计所采用的岭参数和各待求参数的估值与LS岭估计的结果完全相同。对于含有粗差的方案②~④,采用本文的抗差岭估计模型得到的 ΔX分别为0.088 7、0.080 3和0.089 4,各参数估值与真值十分接近,单位权中误差也有明显改善,观测值的精度得到了显著提高。若在抗差迭代过程中始终使用LS岭估计所采用的岭参数则无法达到如此的计算效果,这是由于使用L曲线法求取适合每次迭代的岭参数在理论上更加合理。
4)对于方案②~④,满足收敛条件时抗差岭估计的最终岭参数与LS岭估计的岭参数相比有了较大的变化,这是在迭代过程中反复运用等价权阵分解算法对不正定的等价权阵进行单位化并使用L曲法后所得的最终结果,图1是L曲线法求解这三种方案LS岭估计的岭参数与抗差岭估计的最终岭参数的示意图比较。
5 结语

表1 各方案计算结果Tab.1 Computation result under each scheme

图1 用L曲线法求解两种估计方法的岭参数示意图Fig.1 Determining ridge parameters with two estimation methods by use of L-curve method
抗差迭代过程中岭参数的选取是影响抗差岭估计结果的关键因素,本文将L曲线法引入相关抗差岭估计模型中用于岭参数的求解,针对迭代过程中L曲线法的使用问题,提出等价权阵分解算法对等价权阵进行单位化。算例结果表明,当观测值中不含粗差时,抗差岭估计的结果与LS岭估计等价且明显优于LS估计;当观测值中含有粗差时,LS估计与LS岭估计的结果均失真,而抗差岭估计模型有效克服了系数阵病态和粗差的双重影响,得到的各参数的估值与真值十分接近,观测值的精度也得到了显著提高。
1 隋立芬.抗差岭估计原理及其应用[J].测绘通报,1994,(1):6-9.(Sui Lifen.The principle of robust ridge estimation and its applications in geodetic adjustments[J].Bulletin of Surveying and Mapping,1994,(1):6-9)
2 归庆明,等.抗差泛岭估计[J].测绘学报,1998,(3):211 -216.(Gui Qinming,et al.Robust universal ridge estimation[J].Acta Geodaetica et Catographica Sinica,1998,(3):211-216)
3 常志巧,等.GPS快速定位中病态问题的正则化抗差解法[J].大地测量与地球动力学,2008,(3):83-86.(Chang Zhiqiao,et al.Regularization combined with robust estimation and its application for GPS rapid positioning[J].Journal of Geodesy and Geodynamics,2008,(3):83-86)
4 归庆明,等.抗差部分岭估计及其在GPS快速定位中的应用[J].大地测量与地球动力学,2006,(2):62-65.(Gui Qinming,et al.Robust partial ordinary ridge estimation and its applications in GPS positioning[J].Journal of Geodesy and Geodynamics,2006,(2):62-65)
5 Hansen P C.Analysis of discrete ill-posed problems by means of the L-curve[J].SIAM Review,1992,34(4):561 -580.
6 Hansen P C and O’Leary D P.The use of the L-curve in the regularization of discrete ill-problems[J].SIAM Review,1993,14(6):1 487-1 503.
7 余学祥,等.GPS变形监测数据处理自动化-似单差法的理论与方法[M].徐州:中国矿业大学出版社,2004.(Yu Xuexiang,et al.Automation of GPS deformation monitoring data processing,the theory and method of SSDM[M].Xuzhou:China University of Mining and Technology Press, 2004)
8 Yang Y,Song L and Xu T.Robust estimation for correlated observations based on bifactor equivalent weights[J].J Geodesy.,2002,76:353-358.
9 宋力杰.测量平差程序设计[M].北京:国防工业出版社,2009.(Song Lijie.Programming of surveying adjustment[M].Beijing:National Defence Industry Press,2009)
10 王振杰.测量中不适定问题的正则化解法[M].北京:科学出版社,2006.(Wang Zhenjie.Regularization solutions of ill-posed problem in geodesy[M].Beijing:Science Press,2006)
11 周江文,等.测量误差理论新探[M].北京:地震出版社,1999.(Zhou Jiangwen,et al.The new research of errors theory[M].Beijing:Seismological Press,1999)
APPLICATION OF L-CURVE METHOD TO EQUIVALENT WEIGHT ROBUST RIDGE ESTIMAION MODEL
Wang Bin1,2),Gao Jingxiang1),Liu Chao1,2),Wang Jian1)and Zhou Feng1,2)
(1)China University of Mining and Technology,CESSI,Xuzhou 221116 2)Jiangsu Key Laboratory of Resources and Environmental Information Engineering,Xuzhou221116)
An equivalent weight robust ridge estimation model is derived according to the idea of robust estimation for correlated observations,and then the L-curve method is introduced to this model for the solution of ridge parameters.In the iterative process,equivalent weight matrix may be non positive definite so it can not be unitized through classical Cholesky decomposition.According to the characteristic of bifactor model,an algorithm of equivalent weight matrix decomposition is proposed to solve this problem,then the L-curve method can be successfully used in this process.The calculated example manifests that this model can effectively eliminate the influence of coefficient matrix’s morbidity and gross errors.
robust ridge estimation;L-curve method;ridge parameter;bifactor model;equivalent weight matrix decomposition
1671-5942(2012)03-0097-05
2012-01-08
国家自然科学基金(41074010);江苏省高校研究生科研创新计划项目(CXLX11_0321)
王彬,男,1988年生,硕士生,研究方向:测量数据处理理论.E-mail:rainkingwang881107@163.com
P207
A
