基于经验模式分解的CORS站高程时间序列分析*

张恒璟 程鹏飞

(1)辽宁工程技术大学测绘与地理科学学院，阜新 123000 2)中国测绘科学研究院，北京100830)

基于经验模式分解的CORS站高程时间序列分析*

张恒璟1，2)程鹏飞2)

(1)辽宁工程技术大学测绘与地理科学学院，阜新 123000 2)中国测绘科学研究院，北京100830)

提出基于经验模式分解技术的GPS高程时间序列时频分析方法，并以两个CORS基准站多年连续的高程时间序列数据为对象，获取序列信号的各个本征模态函数分量，研究了信号周期运动的主要贡献分量和序列趋势项的合成与分离的方法。结果表明:在一定的序列区间长度上识别周期项与趋势项才有意义;经验模式分解技术分离的序列趋势项呈现大曲率的非线性形式，与传统的周期函数高程序列拟合线性趋势项存在较大的差异。

经验模式分解;本征模态函数;趋势项;GPS高程时间序列;方差贡献率

1 引言

正确识别并分离序列趋势项对研究GPS高程序列的频谱特性和噪声性质具有十分重要的意义。传统时频信号分析前，须先识别并去除序列的趋势项，例如基于傅里叶分析理论的功率谱估计和小波分解方法。经典方法研究GPS高程时序信号的周期和噪声特性时，事先给定一个具体的周期拟合模型［1，2］，并指定序列存在半年、年、两年等的周期运动和长期的线性趋势运动，通过函数拟合模型，求解各项的振幅相位等特性;接着在分析序列噪声时，从原始序列中去除趋势项和周期项后的残差序列中，分析信号存在的各种噪声特性，但实际上并不是每个GPS高程序列都具有事先设定的多种周期运动特性。因此有必要采用自适应的或者尽量不依赖事先给定特性的序列信号分解方法来识别序列的各种周期运动和趋势项信息。本文引入处理非线性非平稳信号的希尔伯特-黄变换方法［3］，采用经验模式分解(Empirical Mode Decomposition，EMD)和整体经验模式分解(Ensemble EMD，EEMD)，对我国CORS基准站高程序列数据进行分析，获取了本征模态函数分量(Intrinsic Mode Function，IMF)，分析了各个IMF的方差贡献率及对序列运动能量的贡献大小，并研究了合并和提取序列高程运动趋势项的方法。

2 经验模式分解技术

2.1 EMD分解原理

经验模式分解是基于非线性、非平稳数据的自适应时频信号分解方法，通过不断地“筛选”，将原始时间序列信号分解为一系列频率由高到低的本征模态函数分量和残差项，分解产生的IMF函数需满足两个条件:一是待分解信号中极值点的个数与过零点的个数相等或至多相差1;二是在任意点上，由局部极大值定义的上包络线与局部极小值定义的下包络线的均值为零。分解的具体过程为［4，5］:

1)搜索原始信号所有的极大值点和极小值点，用三次样条函数拟合所有极大值点得到上包络线，同理得到下包络线，取上下包络的均值作为原始序列的平均包络m1(t);从原始序列中扣除该平均包络得到新的序列信号h1(t)=X(t)-m1(t)。如果h1(t)满足IMF的条件，则作为第一个分解得到的本征模态函数分量，否则以h1(t)作为信号，继续寻找其上下包络线并求出平均包络m2(t)，得到新信号h2(t)=h1(t)-m2(t)，迭代k次后直至hk(t)满足IMF的条件，将其作为第一个IMF分量IMF1(t)。

2)计算残余分量r1=X(t)-IMF1(t)，将r1作为信号，重复第一步的分解，得到第二个IMF分量IMF2(t)。

3)重复1)、2)步，直至残余分量满足分解中止的条件:即残余分量为单调变化的残差序列不能再分解出本征模态函数为止。原始信号经过n次分解后，可描写为:

这种分解基于数据的局部特征，与傅立叶频谱分析分解成恒定振幅与频率的一系列正弦函数和小波分解需预先给定基函数相比，EMD是一种自适应的分解方法。

2.2 整体经验模式分解

EMD分解的缺点之一是模式混叠现象:一个IMF分量包含着尺度互异的信号，或者尺度相似的信号存在于不同的IMF分量，这种现象主要是由于信号中断引起的，不仅混淆了信号的时频分布特性，更重要的使信号IMF分量的物理意义变得不清晰。为了减弱模式混叠现象的影响，文献［6］在EMD分解基础上提出了整体经验模式分解方法(EEMD)，一种噪声辅助的数据分析方法(noise-assisted data analysis，NADA)，基本思路是在分解之前，将原始序列信号加入白噪声，生成待分解信号，即

下标i表示第i次EMD分解。

白噪声与原始信号的标准差之比例如可以设定为0.1，经过EMD分解后生成一系列的IMF分量;由于每次随机生成的白噪声都是不同的，这样可以通过重复上面的分解过程，得到信号的多次EMD分解的IMF分量，将对应分解尺度相同的IMF分量取平均，即得到了最终信号分解的IMF分量。文献［6］建议整体平均的次数取100，而噪声与信号的标准差之比可以取0.1、0.2、0.4等。本文最大分解层数n设定为:

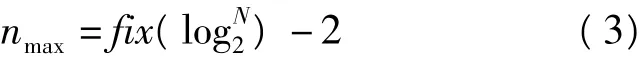
其中N是序列长度，实验采用的序列从1999—2010，共约4 000个数据点，因此得到的最大分解层数(IMF分量的个数)不超过10。这样就存在序列过度分解或分解不完全两种情形，从实验的几个CORS站高程序列分解效果来看，剩余的残差项均是单调的趋势，符合EMD分解要求，不存在分解不完全的情形，而过度分解的情形需要对邻近残差项的IMF分量与残差项合并，来判断合并后的趋势项是否仍然单调变化。

2.3 序列趋势项的定义

传统序列趋势项是基于固定的数学模型定义，比如GPS时间序列常用的周期拟合模型为:

并由式(4)拟合出序列的常数项、线性速率项、周期项(年和半年周期)。式中，ti(i=1，…，N)是以年为单位的时间，以每日解构成坐标时间序列，待求系数a和b为序列线性趋势项，c、d和e、f分别为年周期和半年周期项的系数。

更复杂的情形，在上述模型中考虑各种原因引起的阶跃式坐标突变(例如远场大地震引起的同震位移、由于仪器或天线变更引起的位移、甚至由于某种不清楚原因引起的点位变化等)修正项，这是目前处理GPS时间序列常用的拟合模型。该模型扣除了线性速度项和常数项后的序列，是下一步时序信号频谱和噪声分析的基础，比如基于传统傅里叶理论的功率谱分析技术和目前常用的小波分解技术等。

文献［6］指出，趋势应该是序列信号的内在特性之一，是序列的固有成分，内在特性要求趋势项的定义应该具有自适应性，应基于序列数据本身去分离，而不仅仅是用一个指定的函数模型去拟合和扣除。同时为区分趋势项和长周期项，趋势项的定义必须被限定在给定的序列尺度上，并且至多包含一个极值点。基于上面的考虑，文献［7］给出了趋势项的定义，即:趋势项是一个内在的单调拟合函数，或在一个给定的序列数据区间上至多有一个极值点的函数，“给定的序列数据区间”可以是整个序列，也可以是序列数据的一部分。

3 实验分析

3.1 EMD/EEMD分解IMF分量

对GPS高程序列数据分别采用EMD和EEMD两种分解方法，获取IMF分量。EEMD方法又设计了3种方案，整体平均的次数选用了文献［6］的推荐值100，加入的白噪声与原始序列信号的标准差之比分别取0.1、0.2、0.4，下面以EEMD01、EEMD02、EEMD04分别代表这3种EEMD分解方案。统计任一IMF分量的方差公式为:=E2(X)-(E (X))2，若X为有限长度的数据序列，则可统计出方差的估值。方差贡献率是各个IMF分量的方差与分解得到的IMF分量方差之和的百分比。IMF分量方差贡献率的大小反映了该频率的分解信号在整个序列信号运动能量中的贡献大小。

图1(a)、(b)分别是BJFS(北京房山)和URUM (乌鲁木齐)站采用 EMD/EEMD01/EEMD02/EEMD04 4种分解方案的IMF分量和残差，限于篇幅未给出高频的IMF1～5曲线。由公式(3)可知分解得到的IMF分量个数不超过10，从IMF1～10本征模态分量信号频率依次降低，周期依次增大。

图2是BJFS和URUM两个基准站采用EMD/ EEMD01/EEMD02/EEMD04 4种方案统计得到的各个IMF分量中误差和方差贡献率。

BJFS站分解后的IMF1～3是高频分量，IMF4和IMF5是近似月周期和双月周期信号，但信号的振幅和方差较小，在整个序列信号中所占的比重较小。IMF6、7两个信号分量的方差贡献率之和达到50%以上，是序列的主要周期运动贡献项，即BJFS站的周期运动以季节性变化和年周期变化为主。两种分解方法得到的IMF6分量整体呈现季节性的周期变化，IMF7分量整体呈现明显的年周期变化;但EMD分解与3种EEMD分解方案的方差贡献率出现较大差异，EMD分解的IMF6、7方差贡献率分别是25%与28%，EEMD分解分别是12%与40%左右，两种技术得到的IMF6与IMF7方差贡献率之和几乎保持不变，其他本征模态分量的方差贡献率基本相等。从图1(a)明显看出，EMD分解得到的IMF6季节性信号在横轴2003—2006区间上出现了明显的年周期信号，EMD分解得到的IMF7年周期信号在横轴2003—2006区间上出现了明显的两年周期信号，说明EMD技术分解时部分IMF6信号被分解到IMF7分量上，这是由于模式混叠现象引起的，在图1(a)中以椭圆部分表示。IMF8分量对应着明显的两周年运动，但其方差贡献率和信号振幅相对较小。IMF9和IMF10分量振幅在5 mm之内，是信号分解的长周期还是属于过度分解的残差信号，在趋势项合并部分做进一步的分析。本文也设计了采用相同的EEMD方案对BJFS站多次分解的试验，结果表明每次试验之间低频的本征模态分量IMF6、7的方差贡献率出现了0.5～1.9%的微小变化，但是EMD的分解结果唯一，分析原因可能是EEMD分解时每次加入的白噪声变化引起的，这也说明了EEMD技术仍存在着分解不唯一的缺点，需进一步的研究和完善EEMD分解算法。

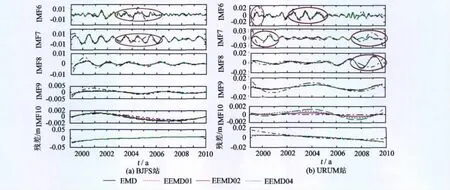
图1 IMF6～10分量与残差项Fig.1 IMF6-10 components and residuals

图2 IMF分量中误差与方差贡献率Fig.2 RMS and contribution rate of variance of each IMF

URUM站3种EEMD分解结果一致性很好，与EMD分解结果相比在中低频IMF分量上有一定的差异。IMF1～3是分解得到的高频信号，这3个分量方差贡献率之和在20%左右，相对于BJFS站这3个高频分量的方差贡献率之和达到35%，GPS时间序列中高频信号一般被认为是序列所含的噪声，从这个角度上可认为URUM站高程序列信号中噪声含量明显低于BJFS站。IMF4分量周期大约是1个月，IMF5分量周期大约是两个月。两种分解技术得到的IMF6分量整体上呈现近似季节性和半年周期变化的信号，但在横轴2002—2005区间上产生了明显的年周期信号。两种分解技术得到的IMF7分量均呈现明显的年周期变化，但 EMD分解方法在IMF7序列的两端产生了两周年的信号。两种分解技术得到的 IMF8整体上是近似2周年信号，但EMD分解在最右侧产生了周期超过3年的分解信号。EMD分解在IMF6～8 3个分量均出现了模式混叠现象，虽然EEMD技术可以减弱模式混叠的影响，但从URUM站IMF6分量的分解结果可知，EEMD仍会出现频谱混叠，需要对EEMD分解技术进一步的研究。从方差贡献率指标定量分析:IMF6～8 3个分量EMD分解的方差贡献率分别是32%、35%、4%，EEMD01和EEMD02方案分解结果几乎完全相同方差贡献率分别是21%、20%、21%，两种分解技术得到的3个分量方差贡献率之和在62～71%之间，说明URUM站的高程运动以季节性、年、两年为主要周期。

3.2 趋势项合成

图3、图4分别为BJFS和URUM站的趋势项合成。

BJFS站IMF9、10分量的中误差在0.8 mm左右，方差贡献率为1.1～1.7%，这两个本征模态分量在整个序列运动中所占的比重很小。从趋势项合成图3可知，最后的两个本征模态分量IMF9、10一起与分解的残差项合并后，曲线几乎保持原有的单一变化趋势，说明IMF9、10分量属于过度分解，也有可能是以目前序列数据的尺度还无法识别的更长周期项，因此在研究的序列区间尺度上IMF9、10分量应归于分解的残差，一并作为序列趋势项处理。

URUM站4种不同的分解方案对应的本征模态分量IMF10中误差均在0.5mm左右，方差贡献率在0.1～0.6%之间，在整个序列运动中所占比重几乎可忽略不计。从趋势项合成图4可知，最后一个模态分量IMF10应归于过度分解产生的分量，与残差合并一起作为趋势项处理。加入IMF9分量之后的趋势项呈现明显的周期振荡，周期近似为序列长度的一半5.5年，加入IMF8合成后的趋势项周期更小且振幅显著增大，说明IMF8、9分量不能作为序列的趋势项，而应当归于序列运动较明显的周期项分量，只是其振幅较小。

4 讨论和总结

1)采用EMD/EEMD方法，获取频率从高到低的IMF分量，可明显分解出GPS高程序列信号的趋势项和周期项。从两个基准站例子可知，分解后的低频IMF分量为高程时间序列信号的周期运动给出了清晰的解释，包含了明显的1个月、2个月、季节性、年周期变化、两周年周期变化与长周期变化因素，半周年项运动信号并不显著，季节性和年周期变化是高程运动的主要贡献项;EEMD分解相比EMD可以明显减弱模式混叠对本征模态分量的影响，但并没有完全消除模式混叠现象，同时受EEMD分解时加入白噪声的影响，其分解结果也不唯一。EEMD比EMD方法有较大的优点，但还需要进一步改进EEMD算法。

2)通过比较各个IMF分量的方差贡献率及其中误差大小，可以判断对原始信号是否存在着过度分解的情形，进而合并过度分解的IMF分量与残差项，获得准确的序列趋势项。合并后的趋势项呈现大曲率的曲线变化，而非线性形式，传统对序列趋势项的线性拟合方法存在不足，序列趋势项不仅包括了线性变化，也有暂时无法分离或识别的长周期信号，只有在一定的序列区间长度上探讨并区分周期项和趋势项才有意义。

图3 BJFS站趋势项合成Fig.3 Trend synthetic diagram of BJFS station

图4 URUM站趋势项合成Fig.4 Trend synthetic diagram of URUM station

致谢 感谢台湾中央大学及Wu Zhaohua等人提供的EEMD分解算法，感谢美国麻省理工学院(MIT)和加州大学圣地亚哥分校 Scripps海洋研究所(SIO)及Robert B.King提供研究计算的GAMIT/ GLOBK软件。

1 黄立人.GPS基准站坐标分量时间序列的噪声特性分析［J］.大地测量与地球动力学，2006，(2):31-33.(Huang Liren.Niose properties in time series of coordinate component at GPS fiducial stations［J］.Journal of Geodesy and Geodynamics，2006，(2):31-33)

2 袁林果，等.香港GPS基准站坐标序列特征分析［J］.地球物理学报，2008，51(5):1 372-1 384.(Yuan Linguo，et al.Characteristics of daily position time series from the Hong Kong GPS fiducial network［J］.Chinese Journal of Geophysics，2008，51(5):1 372-1 384)

3 Huang Norden E，Shen Zheng and Long Steven R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.The Roy-al Society，A(1998)454:903-995.

4 Huang Norden E and Shen Samuel S P.Hilbert-Huang transform and its applications［M］.Singapore:World Scientific，2005:2-14.

5 戴吾蛟，等.基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用［J］.测绘学报，2006，35(4):321-327.(Dai Wujiao，et al.EMD filter method and its application in GPS multipath［J］.Acta Geodaetica at Cartographica Sinica，2006，35(4):321-327)

6 Wu Zhaohua and Huang Norden E.Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.Advances in Adaptive Data Analysis，2009，1(1):1-41.

7 Wu Zhaohua，et al.On the trend，detrending，and variability of nonlinear and nonstationary time series［J］.Proc.Natl.Acad.Sci.USA，2007，104(38):14 889-14 894.

8 徐世艳.经验模态分解的时频分析方法及其应用［J］.吉林大学学报(信息科学版)，2009，27(5):487-492.(Xu Shiyan.Time-frequency analysis method and its application based on empirical mode decomposition［J］.Journal of Jilin University(Information Science Edition)，2009，27(5):487 -492)

9 盖强，张海勇，徐晓刚.Hilbert-Huang变换的自适应频率多分辨分析研究［J］.电子学报，2005，33(3):563-566.(Gai Qiang，Zhang Haiyong and Xu Xiaogang.Study of adaptive frequency multiresolution analysis of the Hilbert-Huang transform［J］.Acta Electronica Sinica，2005，33(3): 563-566)

10 徐佳，黄声亨，麻凤海.基于改进HHT理论的大型桥梁动态特性分析［J］.武汉大学学报(信息科学版)，2010，35(7):801-805.(Xu Jia，Huang Shengxiang and Ma Fenghai.The dynamic characteristics analysis for the large bridge based on the improved Hilbert-Huang transformation［J］.Geomatics and Information Science of Wuhan University，2010，35(7):801-805)

ANALYSIS ON TIME SERIES OF TWO CORS STATIONS’HEIGHT BASED ON EMD

Zhang Hengjing1，2)and Cheng Pengfei2)

(1)School of Geomatics of Liaoning Technical University，Fuxin 123000 2)Chinese Academy of Surveyingamp;Mapping，Beijing100830)

The time-frequency analysis method base on EMD(empirical mode decomposition)for GPS height time series is put forward.Taking two national CORS stations’GPS height time series as an example，each intrinsic mode function is decomposed and the contribution rate of variance is also calculated.The problem of identifying father distinguishing the periodical signals and the trend is emphasizerd.The results indicate that it is only meaningful to distinguish the periodical and the trend signal on certain length of time series’section.The trend based on EMD or EEMD presents with large curvature while the traditional form of periodical fitting function only linear form.

empirical mode decomposition(EMD);intrinsic mode function;trend;GPS height time series;contribution rate of variance

1671-5942(2012)03-0129-06

2012-02-10

国家基础测绘项目(B2551);中国测绘科学研究院基本科研业务费资助

张恒璟，男，1982年生，讲师，博士生，主要从事地球动力学方面的研究.E-mail:zhhj1111@sohu.com

P207

A