基于线性规划模型的运输问题研究

肖满红

（天津机电职业技术学院，天津 300131）

基于线性规划模型的运输问题研究

肖满红

（天津机电职业技术学院，天津 300131）

运输是物流活动核心环节，线性规划是运输问题的常用数学模型。本文结合案例，分析了运输问题的特征及策略，揭示了运输问题中线性规划模型及其变形模型的应用，提供了一类提高物流效益的重要思想方法。

线性规划；运输问题；数学模型；最优化

一、引言

随着经济的发展物流业蓬勃发展，国家之间、地区之间的贸易往来愈发频繁。科学地组织货源进行运输和配送，可以提升效益、优化资源。

运输是物流活动的核心环节，线性规划是运输问题的常用数学模型，利用数学知识可以得到优化的运输方案。本文从分析线性规划模型出发，研究运输问题的最优化问题，探讨提升物流的效益的方法。

线性规划主要是研究在某些限定条件（可用线性等式或不等式表示）下，使某一线性目标函数取得最大值（最小值）的问题。它是定量分析管理活动的重要方法之一。线性规划问题中包含决策变量、目标函数、约束条件三个重要因素。

线性规划的决策变量可以是多个，一般记作 x1，x2，x3，…，xn；

线性规划的目标函数的一般形式为： Max（Min）z＝c1x1＋c2x2＋…＋cnxn

线性规划的约束条件一般用不等式组表示为：

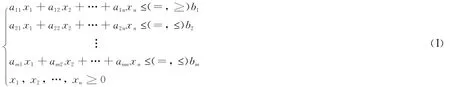
二、运输问题的线性规划模型

运输问题的提出源于如何使物流活动中的运输路线或配送方案是最经济或最低成本的。

1．运输问题的特征

运输问题解决的是已知产地的供应量、销地的需求量及运输单价，如何寻找总配送成本最低的方案；运输问题包含产销平衡运输问题和产销不平衡运输问题；通常将产销不平衡问题转化为产销平衡问题来处理；运输问题的条件包括需求假设和成本假设。

需求假设指每一个产地都有一个固定的供应量，所有的供应量都必须配送到目的地。与之类似，每一个目的地都有一个固定的需求量，整个需求量都必须由出发地满足；成本假设指从任何一个产地到任何一个销地的货物配送成本和所配送的数量成线性比例关系。产销平衡运输问题的一般提法是：

2．运输问题的解决策略

现实生产的情况往往比较复杂，许多实际问题不一定完全符合运输问题的假设，可能一些特征近似但其中的一个或者几个特征却并不符合运输问题条件。一般来说，如果一个问题中涉及两大类对象之间的联系或往来，且该问题能提供运输问题所需要的三类数据：供应量、需求量、单位运价，那么这个问题（不管其中是否涉及运输）经适当约束条件的处理后，基本都可以应用运输问题模型来解决。例如：⑴追求的目标是效益最大而非成本最低，此时仅将表达式（II）中目标函数中的改为即可；⑵部分（或全部）的供应量（产量）代表的是从产地提供的最大数量（而不是一个固定的数值），此时只需将表达式（II）中的产地约束中部分（或全部）的“”改成“”即可；⑶部分（或全部）的需求量（销量）代表的是销地接收的最大数量（而不是一个固定的数值），此时只需将表达式（II）中的销地约束中的“”部分（或全部）改成“”即可；⑷某些目的地的同时存在最大需求和最小需求，此时的解决办法是将表达式（II）中的相应的销地约束中的“”一个式子分解成“”最大需求和“”最小需求的两个式子即可；⑸某些配送中不能使用的出发地—目的地组合，此时的处理方法是添加一个新的约束条件xij＝0。

三、运输问题解决示例

例1（产品运输）甲公司是一拖拉机生产商，有A1、A2两个分厂，将生产的拖拉机用大卡车把它们运送到三个经销地B1、B2、B3。表1中给出各分厂的生产能力、各经销地的需求量和每辆拖拉机从每个分厂到每个经销地所需的运输成本（单位：元）。问应如何调运，才能使得总运输费用最小，最小费用是多少？

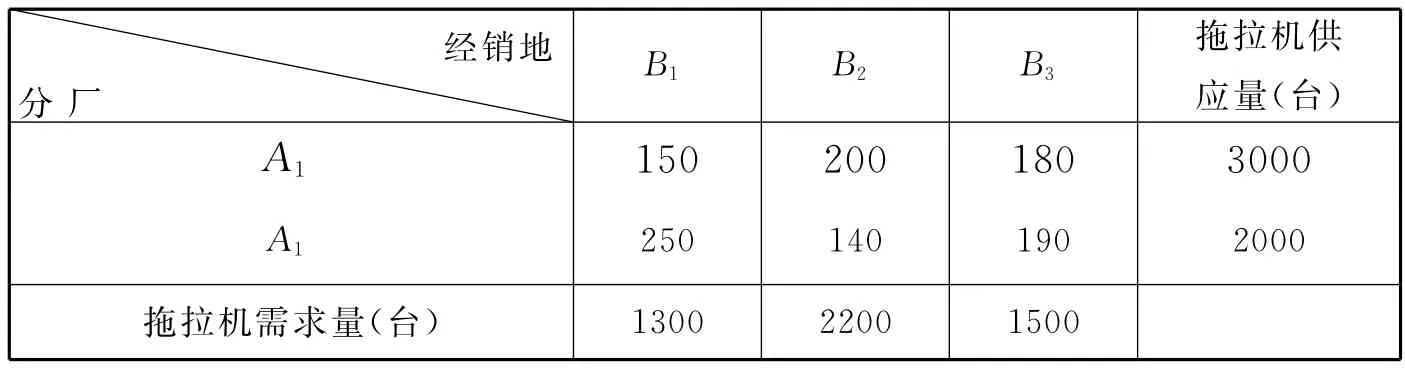
表1 各分工厂到各经销地的拖拉机运价（元／台）

解 由表1知，总产量为3000＋2000＝5000，总销量为1300＋2200＋1500＝5000。由于总产量等于总销量，故该问题属于产销平衡运输问题。

设xij为第i个分厂运往第j个经销地的拖拉机台数（i＝1，2；j＝1，2，3）。则

夕照轻阴郭，回车访枣花。 山门分野色，经阁带林霞。 香篆穿帘细，旛风曳柳斜。 摩娑红杏卷，觞咏想王查。[5]

目标函数为： Min z＝150x11＋200x12＋180x13＋250x21＋140x22＋190x23．

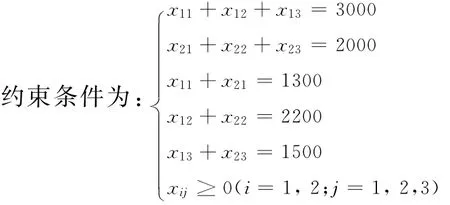
利用Lingo8．0（或Excel）进行计算，不难得最优解为：x11＝1300，x12＝200，x13＝1500，x21＝0，x22＝2000，x23＝0； 由此得到最低的总运输费用为785000元。

例2（学区学生入学的划分）某学区由五个居民区和三所学校组成，学校设专门校车接送学生。各学校的容量如表2所示，各居民区的学生人数如表3所示；各居民区的学生到相应学校的校车费用如表4所示。试问应怎样给各个学校分配儿童，才能实现学区管理者实现使校车接送所花费用最低的目的？表4 校车费用表（单位：元）

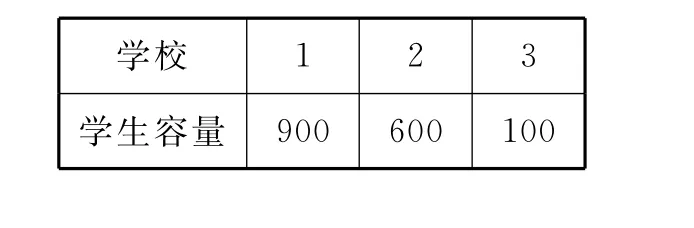
表2 各学校的学生容量

表3 各居民区的学生人数

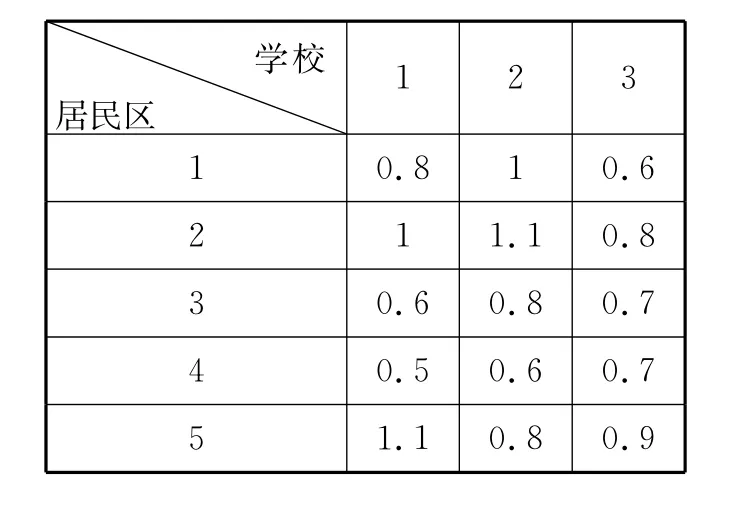
学校居民区1 2 3 1 0．8 1 0．6 2 1 1．1 0．8 3 0．6 0．8 0．7 4 0．5 0．6 0．7 5 1．1 0．8 0．9

解 容易计算出各居民区里的学生总人数为2350，三所学校的学生容量和为2500，二者不相等。根据问题的特点，可将学校看作产地，居民区看作销地。同时，可将校车接送各个学生的费用看作是运输问题的成本，该问题就转化为产销不平衡运输问题。

设xij为校车从第i个居民区将一个学生送往第j个学校的成本（i＝1，2，…，5；j＝1，2，3）。

目标函数为：Min z＝0．8x11＋x12＋0．6x13＋x21＋1．1x22＋0．8x23＋0．6x31＋0．8x32＋0．7x33＋0．5x41＋0．6x42＋0．7x43＋1．1x51＋0．8x52＋0．9x53

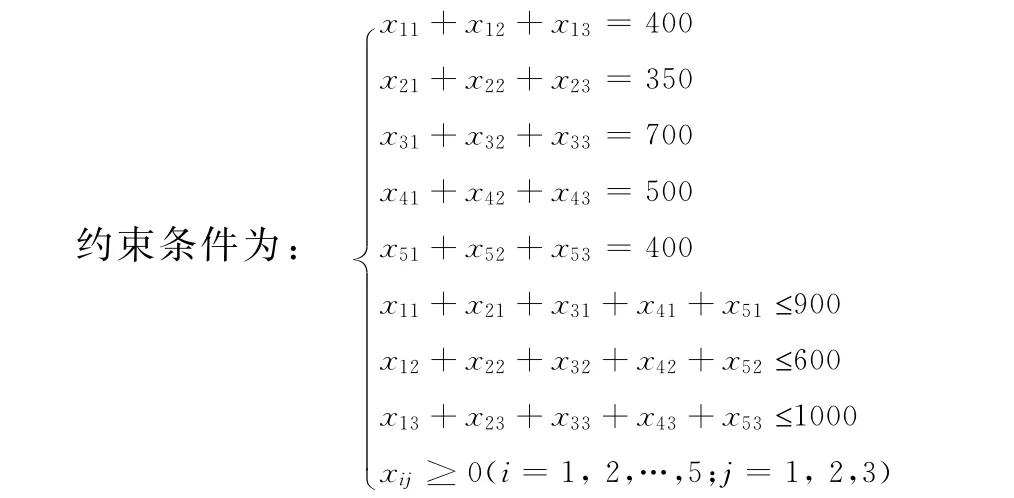
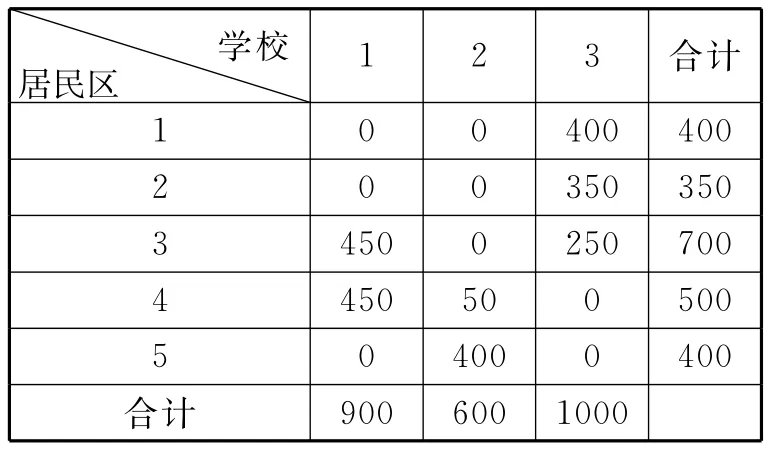
表5 各居民区学生分布数目表

利用Lingo8．0（或Excel）进行计算，不难得最优解为：x13＝400，x23＝350，x31＝450，x33＝250，x41＝450，x42＝50，x52＝200， x11＝x12＝x21＝x22＝x32＝x43＝x51＝x53＝0；此时，接送所花的最低的总费用为1540元。学生划分情况具体如表5所示。

例3（变形的指派问题）一家制药公司，为了提升企业的竞争力，决定加大科研力度，在参考市场调查意见后计划开发5个项目，并邀请4位科学家负责开发。为了保证这些科学家都能够获得他们感兴趣的项目，公司为此建立了一个投标系统。这四位科学家都有1000点的投标点，他们向每一个项目投标，且把比较多的标投向自己最感兴趣的项目，具体投标结果如表6所示：

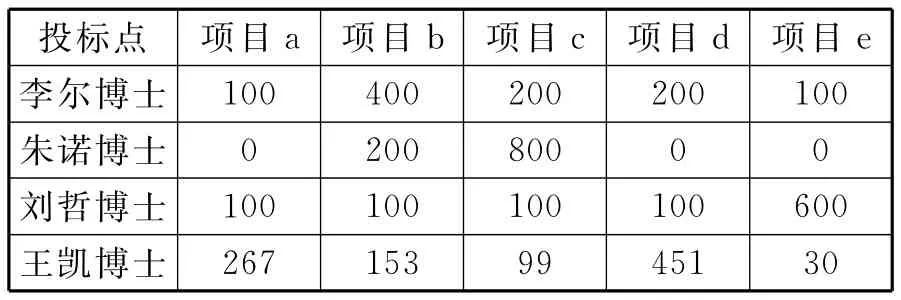
表6 科学家投标结果表

表7 最佳指派方案

原则上，一个人仅能负责一个项目，一个项目也只能由一位科学家来领导，但由于人少项目多，公司决定由朱诺博士或者王凯博士同时负责两个项目。根据投标情况，公司应该怎样指派，才能使得科学家的总满意度最高？

解 指派问题实际上是一种特殊的运输问题，其中出发地是人，目的地是工作，而人负责完成工作时所花费的成本或获得的效益可以看成运输问题中的单位成本。常见的指派问题要求“人数与项目数相等”。而本问题中人数少于项目数，且研究如何使得满意度最高，这样，该模型就成了指派问题的变形模型。

可以根据题意作如下处理：科学家代表运输问题中的产地，项目代表销地，四位科学家投标的标点数看作运输问题中的成本。不难看出，各销地的销量均为1，李尔博士和刘哲博士的供应量都为1，而朱诺博士与王凯博士的供应量都为2，总的供应量（1＋2＋1＋2＝6）大于总的销量（1＋1＋1＋1＋1＝5）。

综上，设xij为第i个科学家负责第j个项目，得到目标函数为：

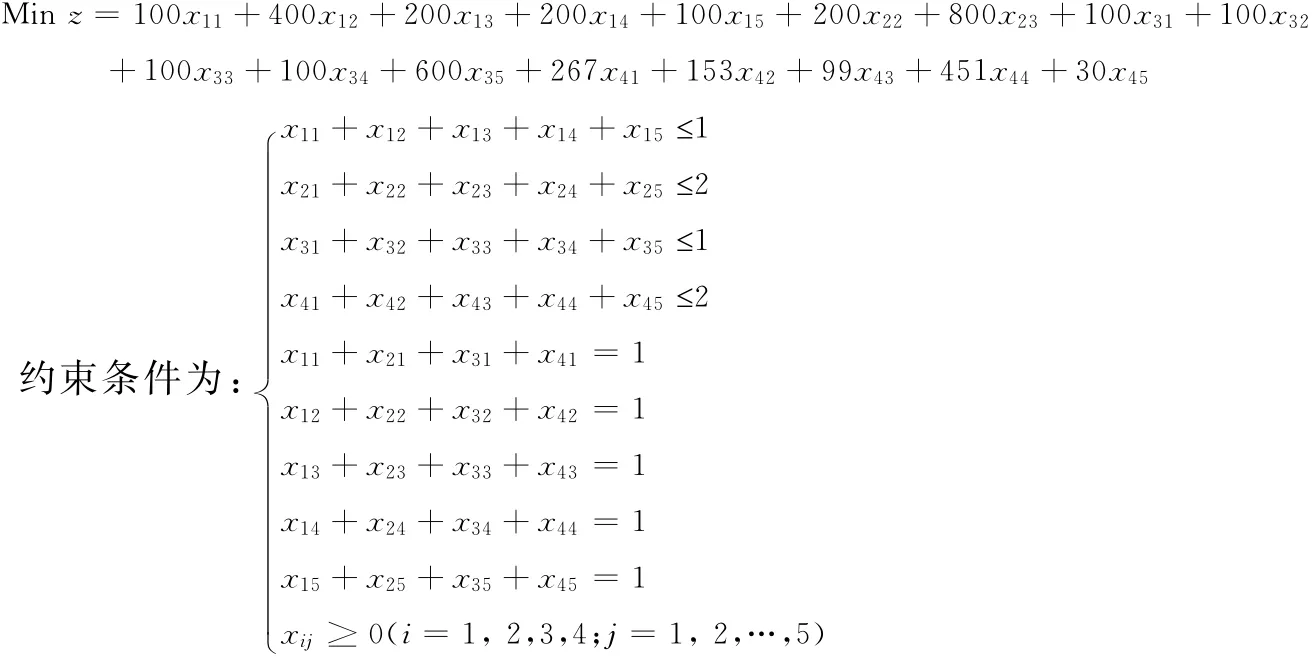
利用Lingo8．0（或Excel）进行计算，不难得最优解为：x12＝x23＝x35＝x41＝x44＝1，其余决策变量均为0。见表7。其中括号内的“是”与“否”代表科学家是否领导他最感兴趣的项目。

总之，以上三个案例都具有启发性，它们揭示了运用线性规划模型解决运输问题的一般思路。在实际问题处理中，要求决策人员准确把握问题中的产销双方以及各自的产量与销量，在此基础上设置好约束条件，同时提炼出运输问题需要的所谓单位成本，建立运输问题的数学模型。

线性规划为决策者解决最优化问题提供了便捷的数学模型，对于企业或个人提升经济效益具有重要的价值。

［1］叶向．实用运筹学［M］．北京：中国人民大学出版社，2006．

［2］胡运权．运筹学基础及应用［M］．北京：高等教育出版社，2008．

［3］刘茂华．线性规划在运输问题中的应用［J］．大庆师范学院学报，2007，（04）．

［4］张家善．线性规划在产销不平衡运输问题中的应用［J］．物流管理，2010，（05）．

Research on the Transportation Problems Based on Linear Programming Model

XIAO Man－hong
（Tianjin Vocational Technical College of Machinery and Electricity，Tianjin，China 300131）

Transportation is a core part of the logistics while linear programming is a mathematical model commonly used in transport．With examples the paper analyzes the transport characteristics and the strategies solving transport problems，reveals the linear programming model and its deformation model applications and provides a series of important ways to improve the efficiency in logistics．

O151．2

A

1673－582X（2012）07－0110－05

2012－05－25

肖满红（1981－），男，湖南省邵阳人，天津机电职业技术学院讲师，从某个事最优化方法机器算法、数值分析研究。