基于正则化方法的不确定参数反演

宋碧宏，邓潮铃，朱蔚蔚，袁 菊，韩 聪

（1.西北核技术研究所，西安 710024；2.重庆大学 土木工程学院，重庆 400045）

结构损伤识别的基本问题是如何从给定的结构力学特性测量中，确定结构损伤的出现、位置和程度，属力学反问题研究范畴。由于实际工程中测量信息的不充分和不准确，使得反问题的解往往是不适定的，也即是解不同时满足下列3个条件：1）解的存在性；2）解的唯一性；3）解的收敛性。在工程实际中反问题的求解都是根据实际问题建立优化目标函数，求反问题的优化解，从而反问题的求解问题可归结为非线性泛函的极值问题。由于结构损伤识别问题的非线性和解的不适定性，使得结构损伤识别问题的求解变得极为困难，因此，研究高效实用的反演方法显得十分重要和必要。

笔者采用正则化迭代反演方法，通过结构的固有频率和振型联立进行结构的损伤识别，并用算例验证该方法的可行性。

1 正则化方法简介

正则化方法是一种行之有效且广泛使用的用于求解病态反问题（不适定性反问题）的稳定近似解的数值方法。反问题的不适定性特性将对整个数值求解产生本质的影响，可以把不适定性问题的数值逼近看成是其扰动数据的解（包括算子扰动和输入数据扰动），因此直接将方程近似求解的标准方法用于不适定性方程时将产生无意义的数值结果。问题病态性的程度可由映射算子的条件数大小来判定，条件数越大则问题的病态性越严重。正则化方法是为处理不适定性反问题而提出的。

所谓正则化（regularization），就是通过对不适定的原问题进行适当的调整，使之变成与原问题相临近的适定问题，从而用该适定问题的稳定解去逼近原问题的不稳定解。

2 镇定泛函（稳定泛函）的构造

线性或非线性参数系统的识别方程可以统一描述为：

F：｛θ｝→｛P｝是Hilbert空间的有界算子。当算子为病态时，可采用Tikhonov正则化方法来构造该问题的有效算法，即将式（1）化为如下的泛函（展平泛函）极小问题：

其中 Ω（｛θ｝）是定义在空间｛θ｝上的镇定（稳定）泛函。Ω｛θ｝与某些先验知识，或是先验解有关。表示欧氏2－范数；λ＞0为正则化参数，决定了残差范数和镇定泛函范数之间的一种协调关系。

在没有任何先验知识的情况下，对于有限维离散的参数识别问题，镇定（稳定）泛函通常可选择为：

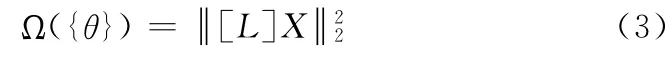
其中，[L]是正则化稳定矩阵，其选择主要考虑算子的条件数和奇异值分布，[L]的不同取法会影响到近似解的精度和稳定性。

在结构系统识别中，结构参数的取值分布往往有一些先验的知识，将这些先验知识构成的参数约束条件取为Tikhonov镇定泛函，从而可以将不适定问题转化为所谓的条件适定问题求解。常用的参数约束条件是给定参数的取值范围，认为参数｛θ｝在某一预估值｛θ0｝（如参数设计值）附近波动，即：

在结构系统识别中，另一个常用的参数约束条件是某些参数的取值接近相等，如可以认为同一构件中各单元的物理参数或同一类型构件的物理参数接近相等。即有：

综合式（4）、（5），参数约束方程可合写为：

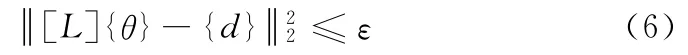
考虑约束条件（6）的参数识别问题（1）可化为如下优化问题求解：

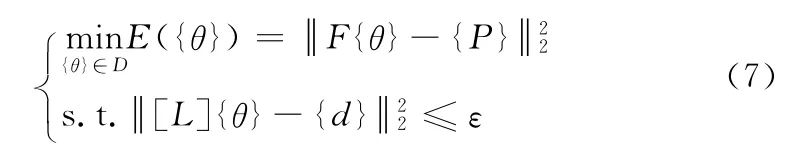
按照Lagrange乘子法，该优化问题等效于正则化问题：

其中[L]／｛θ0｝＝｛d｝。

针对病态不适定问题，Hoerl和Kennard提出了用岭估计的方法来克服矩阵的病态性。它是一种在均方误差意义下优于最小二乘法估计的有偏估计方法。结合式（1）并且对式（2）求导，得到岭估计的解为：

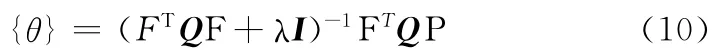
其中｛θ｝为岭估计解；λ为岭参数；I为单位矩阵，Q为权重矩阵；表示欧氏2－范数。

3 Landweber迭代法

数学物理中的反问题往往是不适定的，而不适定问题的求解所面临的本质困难是解的不稳定性，若不通过特殊的方法求解就不会得到合理的结果。Landweber迭代法对于求解大规模问题是十分有利的，而且比较稳定。目前，Landweber迭代法已进一步发展于求解非线性的不适定问题。

Landweber迭代法基于岭估计，其迭代格式为：

4 算例

4.1 平面26杆桁架结构模型

如图1所示的平面26杆桁架结构，杆的截面面积为10－4m2，弹性模量和密度均未知。

图1 平面26杆桁架结构

4.2 区间参数反演

已知前5阶特征值的上下限见表1。

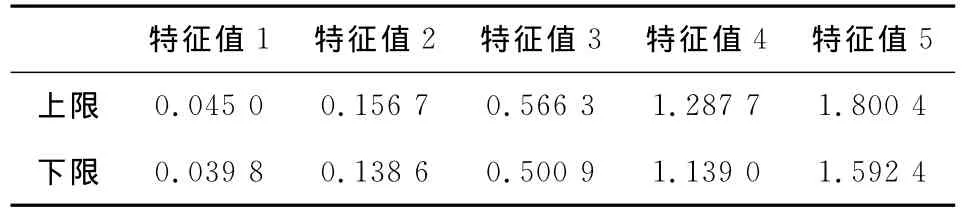
表1 平面26杆桁架前5阶特征值的上下限（×106）

分别对特征值的上下限采用正则化方法，通过L曲线（图2、图3）获得岭参数，经过Landweber迭代法，迭代次数为6次。从而得到结构各个杆件的弹模上下限如表2所示。

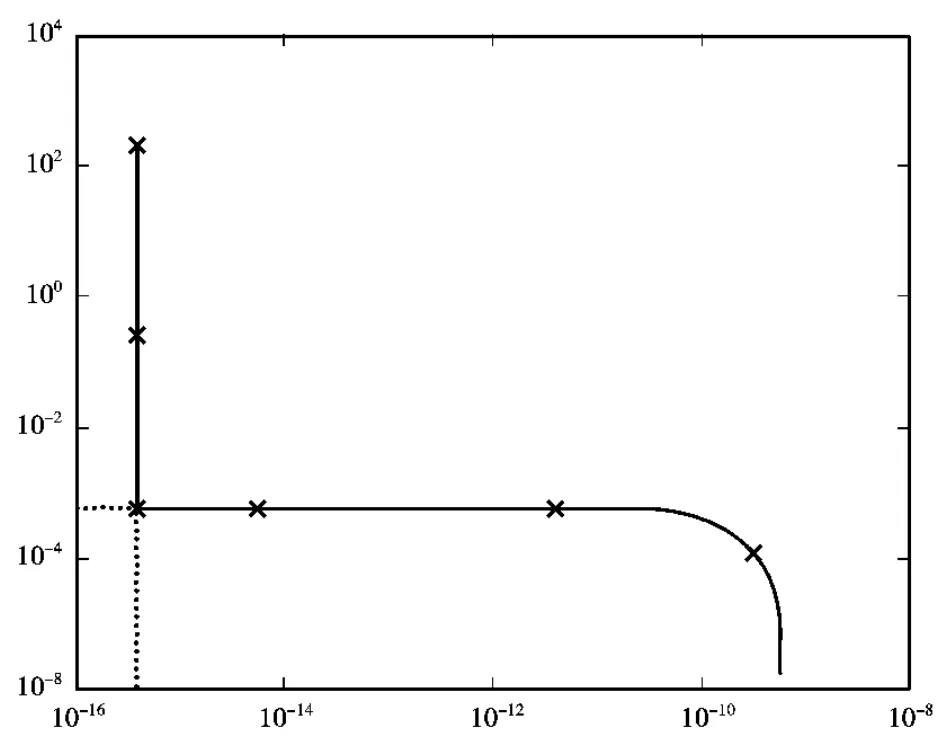
图2 弹模密度上限L曲线

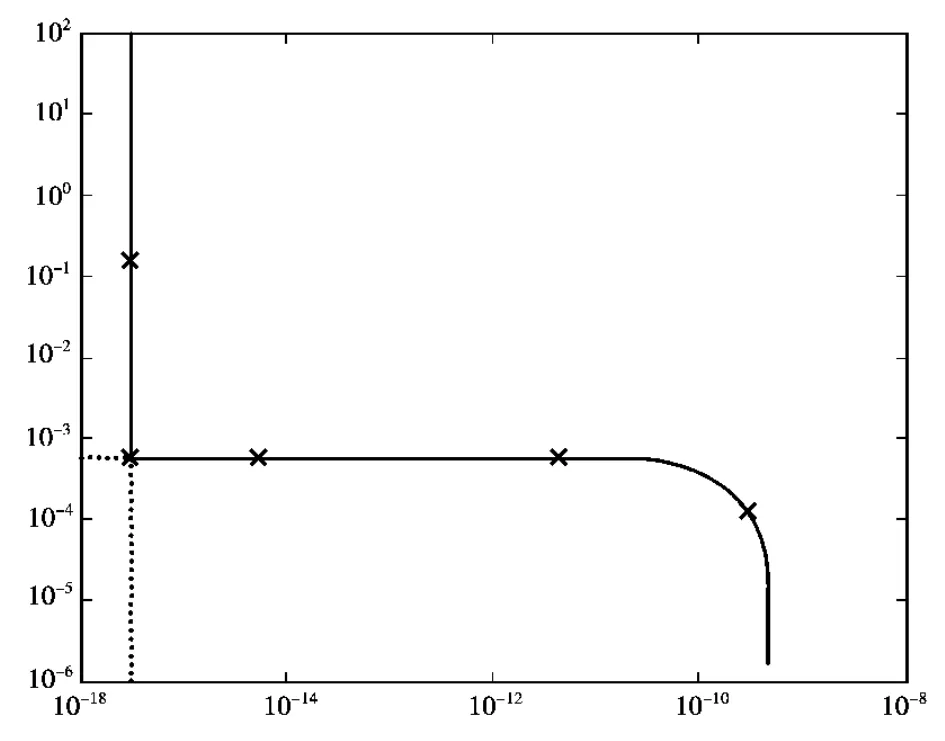
图3 弹模密度下限L曲线

表2 平面26杆桁架各杆件弹模的上下限

在计算过程中，由于弹性模量和质量密度的数量级不同，并且相差较大，故在计算处理过程中，将弹性模量和质量密度统一到较小的数量级上来，这样会在一定程度上降低反问题的不适定性和病态性，从而使反演解达到稳定且收敛。

从计算反演结果来看，特征值的上限反演得到弹性模量的上限，特征值的下限反演得到弹性模量的下限，除此之外，还能看出反演的结果完全与真实解符合，这说明反演很成功，理论得到证明。

[1]Tikhinov A N，Arsenin V Y.Solutions ofⅢ：posed problems[M].Washington：V.H.Winston，1977.

[2]Hansen P C.Rank-deficient and discrete Ⅲ－posed problems：numerical aspects of linear inversion [M].Philedelphia：SIAM，1998.

[3]Eng H W，Hanke M，Newbauer A.Regularization of inverse problemls[M].Dordrecht：Kluwer Academic Publishers，2000.

[4]肖庭延，于慎根，王彦飞.反问题的数值解法[M].北京：科学出版社，2003.

[5]柳春图，陈卫江.缺陷识别反问题的研究状况与若干进展[J].力学进展，1998，28（3）：361-373.LIU Chuntu，CHEN Weijiang.The research state and some progress on inverse problem of flaw identification[J].Advances in Mechanics，1998，28（3）：361-373.

[6]Marin L.Boundary element：minimal error method for the Cauchy problem associated with Helmholtz：type equations[J].Computationel Mechanics，44（2）：205-219.

[7]Hayashi K，Onishi K，Ohura Y.Direct numerical identification of boundary values in the Laplace equation[J].Journal of Computational and Applied Mathematics，2003，152（1／2）：161-174.

[8]Delvare F，Cimetiere A.A first order method for the Cauchy problem for the Laplace equation using BEM[J].Computational Mechanics，2008，41（6）：789-796.

[9]王振杰.测量中不适定问题的正则化解法[M].北京：科学出版社，2006.

[10]金其年，侯宗义.关于迭代Tikhonov正则化的最优正则参数选取[J].高校应用数学学报：A辑，1996，11（3）：32l-328.JIN Qinian，HOU Zongyi.Optimal regularization parameter choice for iterated Tirhonov regularization [J]. Applied mathematics A Jonrnal of Chinese Universities，1996，11（3）：321-328.