岩溶地区径流预报中BP网络的改进

王文梅，孙蓉琳，高 岩

(1.中国地质大学 环境学院，武汉 430074;2.贵州大学资源与环境工程学院，贵阳 550003)

1 研究背景

在岩溶地区，特别是岩溶管道、裂隙、溶洞发育地带，各种岩溶地貌导致地表地下分水岭不重合，流域划分难，流域出口断面总径流量来源的汇水面积、汇水量不确定。径流预报最早采用回归、时间序列分析方法［1－3］，此类方法过于简单，达不到洪水预报精度;之后又发展了适用于湿润地区的新安江模型、陕北模型［4－5］，如今已经很成熟，但对于复杂的岩溶地区，其参数确定困难，预报精度差;为提高径流预报的精度，避免下垫面各种不确定地质、地貌因素影响，人工神经网络预报径流已经成了一种可能。

人工神经网络［6］(Artificial Neural Network，ANN)是一个可自动提取一组预报变量和另一组自变量之间非线性关系的数据处理系统，该网络的建立过程称为人工神经网络的训练过程，通过自适应算法递归迭代求解因变量与自变量之间的非线性关系。BP(Back Propagation)网络是人工神经网络中最普遍、最有效、最活跃的网络结构，可以模拟非线性问题。在国内外已有很多研究者运用人工神经网络进行洪水、径流、水位等预报。

BP神经网络有以下缺点［7］:①具有学习收敛速度缓慢;②不能保证收敛到全局最小点;③网络的学习记忆具有不稳定性;④网络隐含层数及隐含层单元数的选取尚无统一的理论指导。鉴于BP网络的这些缺点，目前有通过寻找最优的输入层影响因子［8－11］，建立不同水期预报模型［12－14］，其目的是为了优化BP网络的输入层因子，但未能克服BP自身缺陷;运用遗传算法、最小二乘法等调整输入层神经元数和权重值［15－17］进行模型优化。以上模型可以避免新安江模型、陕北模型中不确定参数的获取，但从根本上说都没有克服BP网络根据全局误差修改网络权重，使得较大和较小的输出层误差偏大，预报精度不高。

基于BP根据全局误差修改网络权重缺点和径流预报中对大洪水和小洪水预报精度不高的问题，本文采用SPASS软件，进行快速聚类、多元回归分析，消除原始信息中相关性大又对模型解释能力小的信息，调整BP初始权值;采用对数处理方法对逐日降雨量进行对数处理，克服BP根据全局误差修改网络权重的缺陷。最后以岩溶地区径流量预报为例进行可行性验证。

2 BP网络模型

2.1 BP 网络原理

BP网络［18］是一种根据误差，反向传递修正隐层间权值从而达到训练精度要求的多层网络，它由输入层、隐层、输出层构成，每一层之间通过权值因子连接。基本的工作原理是:根据输入层、权值因子输出下一层，输出层又将作为下一层的输入层，以此逐步连接到输出层;通过BP输出层与期望的输出层的误差再反向调整各层的权重，直到达到允许误差范围或超过训练次数结束训练。BP网络的优点在于它不需要知道中间的演变过程，直接是个黑箱模型，通过输入得输出。在实际的复杂问题上，也可以人为地根据重要因素的先验概率调整其在输入层中权值，从而使得模型具有现实性。

BP网络神经元(不同层的输入因子与输出因子)之间的传递函数常用有:Hardlim，purelin，singmoid函数，各自的特点为对数据的处理方式不同［19］。图1是一个经典的常用3层BP网络结构，其中输入节点为R，表示R维输入，隐层节点数为N，隐层传递函数采用Sigmoid，输出节点数为S，表示S维输出，输出层传递函数采用purelin函数。XR表示第R个输入层因子，aN表示第N个隐层因子，YS表示第S个输出层因子，WNR表示第R输入层因子与第N个隐层因子之间的连接权值。

图1 BP神经网络结构图Fig.1 Structure of BP neural network

2.2 BP 算法

BP神经网络的基本核心是BP算法，由正向传播和反向传播组成。杨桂芳［20］等人于2000年在岩溶水库渗透研究中提出正向传播和反向传播过程的公式及各层相关关系表达式。在BP算法中，用于对求和单元进行函数运算的激励函数f常用singmoid函数，该函数分为对数Sigmoid函数(Logsig)和正切Sigmoid函数(Tansig)。本文采用Logsig函数，其形式为

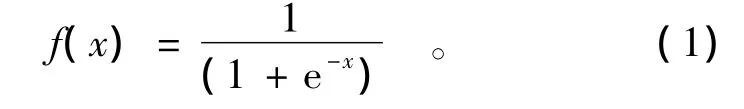
根据Logsig函数的特点，其输入层一般需要将原始数据进行归一化才能作为BP网络的输入值，其原因在于把不同量纲的建模原始数据量纲化以减小不同的数值差异。一般将数据归一化到［0，1］之间，对于有限的训练和验证样本资料而言，不能完全包括所有特性的径流预报，为了使模型对超出训练、样本和验证样本以外的预报数据仍能够归一化到［0，1］之间，使模型适用性更强，本文将建模数据(流域的日降水量、平均日蒸发量、前期流量、出口断面流量)归一化到0.2～0.8之间。归一化的公式为:

式中:xmax为原始数据中最大值;xmin为原始数据中最小值;c为常数;xi为原始数据中第i个数据;yi为归一化后第i个数据;i的取值由样本量决定。

3 实例分析

洪水预报的误差指标采用以下3种:绝对误差、相对误差、确定性系数DC［21］。洪水预报过程与实测过程之间的吻合程度可用确定性系数作为指标，按下式计算:

式中:DC为确定性系数(取两位小数);yc为预报值(m3/s);y0为实测值(m3/s);y0为实测值的平均值(m3/s);n为资料系列长度。DC在0～1之间，越大表示吻合程度越好，如果DC算出负值表示误差太大，计算时选用的方法不合理。

当一次预报的误差小于许可误差时，称为合格预报［21］。降雨径流预报［21］以实测洪峰流量的20%作为许可误差。峰现时间［21］以预报根据时间至实测洪峰出现时间之间时距的30%作为许可误差，当许可误差小于3 h或一个计算时段长，则以3 h或一个计算时段长作为许可误差。合格预报次数与预报总次数之比的百分数为合格率［21］，其公式为

式中:QR为合格率(取1位小数);n为合格预报次数;m为预报总次数。

3.1 六冲河流域概况

乌江属于长江流域，六冲河位于乌江上游西南方向贵州毕节赫章县，六冲河七星关站属于基本水文站，控制的流域面积为2 970km2。七星关站是贵州典型的岩溶代表站，上游还有2个雨量站，分别为水营站和六曲沟站。流域内地势西高东低，具有山高坡陡、河谷深切的特点，降水量西部为951.8mm，中部为1 180.8mm，东部为1 229.2mm，多集中在6－9 月份。

模型采用六冲河七星关站1974－1978年资料作为训练和调整模型样本，以1982年资料作为训练样本。运用SPASS聚类分析，对各年份进行丰水年与平水年划分，对同年进行丰水期和平水期划分，从而建立不同年份不同水期的预报模型。由于资料有限本文只做各年丰水期的模拟。根据贵州六冲河七星关站蒸发、降雨和流量资料，六曲沟站、水营站的降雨资料，其中日降雨量按照算术平均算出。通过SPASS 聚类分析把 5，6，7，8，9，10 月份划分为丰水期，3，4，11 月份为平水期，1，2，12 月份为枯水期。并计算出不同时期不同参数的c值见表1。

表1 丰水期c值计算表Table 1 Calculation results of c value in wet season

3.2 原始数据未做处理前仿真

通过输入1974－1978年不同时期实际的降水量、蒸发量、前期流量进行BP训练，采用经典的3层BP网络模型，选择Sigmoid为隐层传递函数，purelin函数为输出层传递函数，traindx为训练函数，训练最大迭代次数为10000，goal误差目标0.001，隐层数从1开始逐步增加训练模型，其它参数采用BP网络默认值，最后通过1974－1978年训练所得径流量与实测径流量的误差，选择最优的隐层数确定模型.根据训练模型进行预报，将输出数据反归一化得到1982年丰水期预报值为例，结果见图2。

图2 1982年改进前仿真与实测径流量比较图Fig.2 Comparison of simulated runoff and observed runoff before model modification in 1982

通过上述仿真结果分析:仿真结果与实测流量过程线走势一样，证明BP神经网络在岩溶地区建立降雨—径流预报模型具有一定的可行性。但是发现洪峰值的仿真效果和起落峰时流量过程线吻合不好。这主要是由于经典的BP算法，网络训练是根据全局误差修改网络权重的，这种权重修改方法很难控制洪峰流量的变化规律，所以经过训练的网络对中、低流量的预报精度相对较高，而对洪峰的预报精度往往低一些;同时网络默认的初始权值是随机生成的，收敛的速度慢，使模型与真实之间不完全一致。鉴于这样的弊端，本文试图用回归分析对BP网络各初始权值进行调整，用对数处理方法降低洪峰流量与平均流量之间的数量级。

3.3 调整BP网络初始权值

BP网络中各隐层训练的初始权值是随机生成的，具有偶然性，本文通过岩溶地区降雨、径流、蒸发之间的关系，运用SPASS软件，建立各站降雨量、流域日蒸发量、前期径流量之间的相关关系作为BP网络中各隐层初始训练权值，可以优化初始的BP网络结构，使模型预报效果更好。并通过统计学中的DW，VIF，F检验确定回归方程:

式中:x1为前1 d径流量;x2为前期2 d径流量;x3为前期3 d径流量;x4为日蒸发量;x5为水营站逐日降雨量;x6为六曲沟站逐日降水量;x7为七星关站逐日降水量;~y为流域出口断面预测径流量。

其中要说明的是:回归方程中没有体现x7，其原因是七星关站正好是流域出口断面上的水文站，不能反映流域中的降雨量;没有x2，x3，其主要原因是所选取的流域面积不大，加上贵州属于高原地区，坡降大，其汇流时间小于预报时间1 d。

3.4 流量资料对数处理

由于BP算法顾及全局，而对局部的差异性数据纠正量少，那么对于洪峰而言本身就是局部变化量大的数，BP网络的结构决定了其误差一定是很大的。如果将全部的径流量数据取对数后再进行训练和仿真，这样可以有效地缩小各个逐日径流量数据之间的数量级，使得BP网络训练时局部误差变化变小，可以有效地校正洪峰处的误差。从丰水期逐日流量数据中可以看到，最大流量在707 m3/s，最小流量为6.9 m3/s，相差数量级为2;通过对数处理后，最大流量为2.849 4 m3/s，最小流量为0.838 8 m3/s，属于同一个数量级。

同时在未用对数处理前，逐日流量的归一化值大多集中在0.2～0.3之间，通过对数处理后，归一化值在0.2～0.8之间分布均匀。通过这样处理BP在训练时就可以有效地顾及洪峰流量。

3.5 处理后BP仿真

通过网络权值的调整和流量对数处理后的训练同样以1974－1978年的数据做训练样本，以1979－1983年的数据做仿真。模型中初始权值按照回归方程系数给定，其它参数不变，通过训练生成模型预报1982年的径流过程结果见图3。

图3 1982年改进后仿真与实测径流量比较图Fig.3 Comparison of simulated runoff and observed runoff after model modification in 1982

从图3可以看出，改进的模型在岩溶地区的径流预报可以有效地校正中等及以下洪峰。根据1982年，大于丰水期平均流量76.64 m3/s的洪峰共有15次。结果见表2。

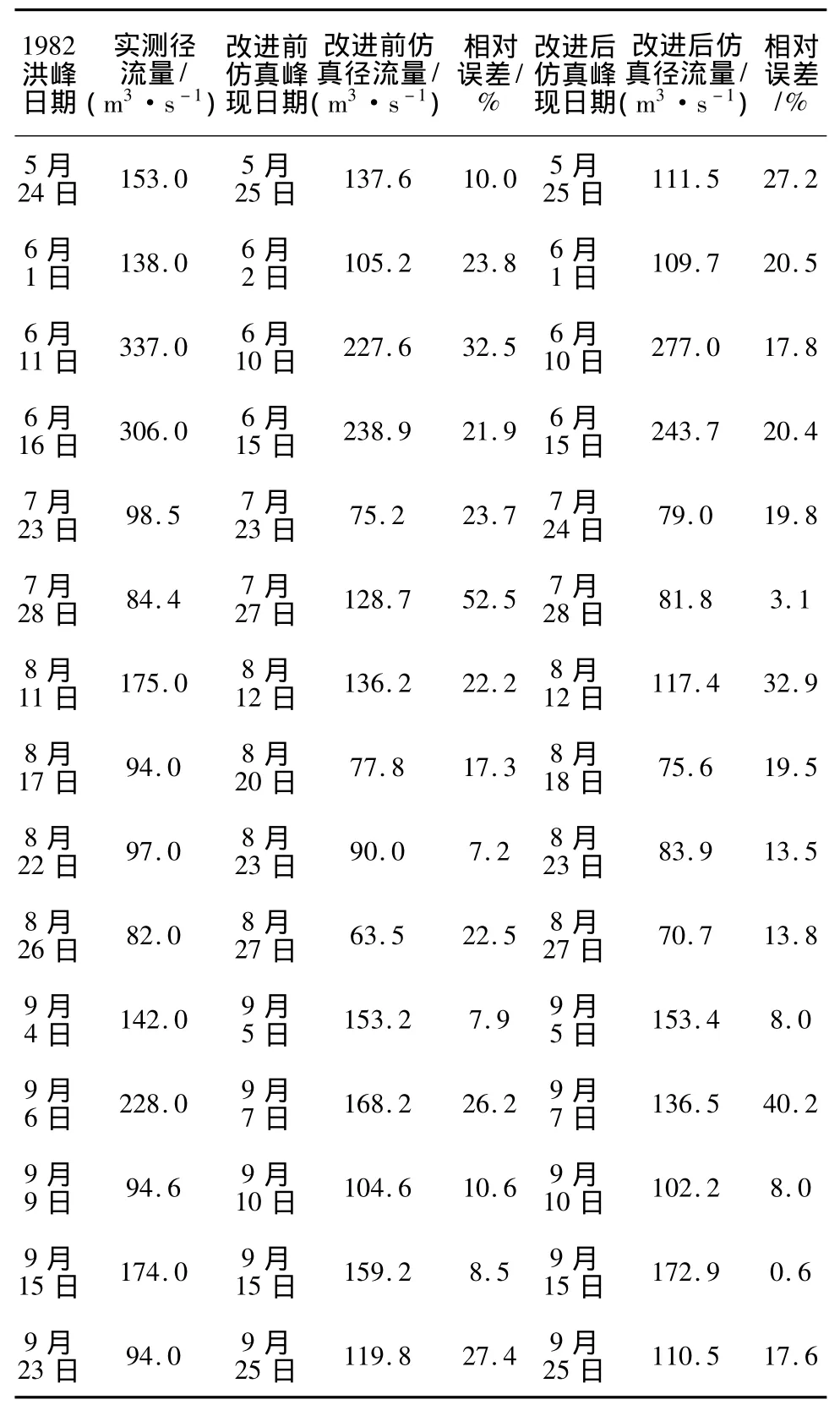
表2 对数处理和初始权值修正改进前后的仿真径流量和峰现时间比较表Table 2 Comparison of simulated runoffs and peak dates before and after logarithm processing and initial weight modification

由表2的结果可以看出:通过改进后的BP网络模型可以有效地提高径流量特别大和径流量特别小的洪峰预报精度;但是，也降低了洪峰流量适中的预报精度。其原因在于BP算法通过全局误差调整网络传递权值，对数处理使数量级降低，会减小中等洪峰在全部洪峰中的影响权值，增加大洪峰和小洪峰的影响权值。

本文进行的是逐日径流量预报，预报时段为1d，故按照峰现时间许可误差要求，峰现时间允许值为1 d。对于洪峰流量预报以实测洪峰流量的20%作为许可误差。从表2和表3可以看出改进前后各项指标的精度值，表现为改进后峰现时间、洪峰流量精度提高，DC系数变大，误差减小。

总体上，通过对径流量进行对数处理，降低预报对象的数量级，可以提高大洪峰和小洪峰的洪峰流量预报精度;通过SPASS软件对BP训练赋初始权重进行建模，可使洪峰涨落过程与实际径流过程更加吻合，同时提高洪峰预报时间合格率，这是因为网络初始权值的调整提高了模型对实际降雨－径流过程的吻合性(表3)。

表3 1982年径流量预报评价指标Table 3 Evaluation indexes of runoff forecasting in 1982

4 结论

本文通过改进的BP算法，建立了岩溶地区流量预报模型，主要研究成果和不足如下。

4.1 成 果

(1)BP网络是一个黑箱模型，通过BP网络在岩溶地区径流预报中的应用，可以避免常用的新安江模型、陕北模型中的参数在地下岩溶管道、裂隙发育岩溶地区难以确定的弊端。

(2)对于岩溶地区的降雨径流非线性问题，前期通过SPASS软件的线性处理调整BP网络初始权值，使模型在训练中提早知道了降雨径流的时间过程，有效地提高降雨径流中时间的预报精度。

(3)通过对径流量进行对数处理，可以降低原始数据之间的数量级，从而提高径流量大和径流量小的洪峰流量，这为运用BP进行极端气候中干旱和洪涝灾害的预报提出一种可能的方法。

4.2 不 足

(1)降雨、蒸发在流域上有其差异性，雨量站、流量站、水文站的分布不均匀，因此建立降雨－径流模型时，在计算逐日平均降水量，逐日平均蒸发量时，应按照地形图进行加权计算。

(2)数据量太小，未能建立丰水年、枯水年各自的径流预报模型。

［1］范钟秀.中长期水文预报［M］.南京:河海大学出版社，1999.(FAN Zhong-xiu.Mid-and-Long-Term Hydrological Forecasting［M］.Nanjing:Hohai University Press，1999.(in Chinese))

［2］丁 晶，邓育仁.随机水文学［M］.成都:成都科技大学出版社，1988.(DING Jing，DENG Yu-ren.Stochastic Hydrology［M］.Chengdu:Publishing House of Chengdu University of Science and Technology，1988.(in Chinese))

［3］刘 勇，陈元芳，王银堂，等.基于OSR-BP神经网络的丹江口秋汛期径流长期预报研究［J］.水文，2010，30(6):32－36.(LIU Yong，CHEN Yuan-fang，WANG Yin-tang，et al.Long-term Forecasting for Autumn Flood Season in Danjiangkou Reservoir Basin Based on OSR-BP Neural Network［J］.Journal of China Hydrology，2010，30(6):32－36.(in Chinese))

［4］许明一.渭河流域水文模型研制及应用［D］.南京:河海大学，2007.(XU Ming-yi.Study and Application of Hydrological Model for Weihe River Basin［D］.Nanjing:Hohai University，2007.(in Chinese))

［5］邹文安，刘兴富，刘宝涵.新安江模型在洪水预报中的应用［J］.吉林水利，2000，(11):5－6.(ZOU Wen-an，LIU Xing-fu，LIU Bao-han.Application of Xinanjiang Model to Flood Forecasting［J］.Jilin Water Resources，2000，(11):5－6.(in Chinese))

［6］黄海洪，孙崇智，金 龙.基于主分量的神经网络水位预报模型应用研究［J］.南京气象学院学报，2005，28(1):58－63.(HUANG Hai-hong，SUN Chong-zhi，JIN Long.Neural Network Prediction Model of Xijiang River Water Level Based on Principal Component Analysis［J］.Journal of Nanjing Institute of Meteorology，2005，28(1):58－63.(in Chinese))

［7］杜 刚.改进BP神经网络在地下水质评价中的应用［D］.上海:上海师范大学，2007.(DU Gang.Application of Improved BP Network in Groundwater Quality E-valuation［D］.Shanghai:Shanghai Normal University，2007.(in Chinese))

［8］李根义，朱学愚，钱家忠，等.实数编码遗传算法优化的神经网络模型在岩溶水水位预报中的应用［J］.南京大学学报(自然科学)，2001，37(3):324－326.(LI Gen-yi，ZHU Xue-yu，QIAN Jia-zhong，et al.Neural Network Model Based on RNCGA and Its Application to Karst Groundwater Evaluation［J］.Journal of Nanjing U-niversity(Natural Sciences)，2001，37(3):324－326.(in Chinese))

［9］占玉林，王长耀，牛 铮.基于BP网络的降雨水位预报模型应用研究［J］.中国科学院研究生院学报，2007，24(1):81－85.(ZHAN Yu-lin，WANG Changyao，NIU Zheng.An Application Research of Rainfall-Water Level Forecast Model Based on BP Network［J］.Journal of the Graduate School of the Chinese Academy of Sciences，2007，24(1):81－85.(in Chinese))

［10］朱星明，卢长娜，王如云，等.基于人工神经网络的洪水水位预报模型［J］.水利学报，2005，36(7):806－811.(ZHU Xing-ming，LU Chang-na，WANG Ru-yun，et al.Artificial Neural Network Model for Flood Water Level Forecasting［J］.Journal of Hydraulic Engineering，2005，36(7):806－811.(in Chinese))

［11］REN M L，WANG B D，LIANG Q H，et al.Classified Real-time Flood Forecasting by Coupling Fuzzy Clustering and Neural Network［J］.International Journal of Sediment Research，2010，25(6):134－148.

［12］JU Q，YU Z B，HAO Z C，et al.Division-based Rainfall-Runoff Simulations with BP Neural Networks and Xinanjiang Model［J］.Neurocomputing，2009，72(8):2873－2883.

［13］LUK K C，BALL J E，SHARMA A.A Study of Optimal Model Lag and Spatial Inputs to Artificial Neural Networks for Rainfall Forecasting［J］.Journal of Hydrology，2000，227(1):56－65.

［14］SINGH PANKAJ，DEOM C.Suitability of Different Neural Networks in Daily Flow Forecasting［J］.Applied Soft Computing，2007，7(6):968－978.

［15］尚晓三，王栋.贵州典型岩溶流域日降雨径流过程模拟研究［J］.中国岩溶，2009，28(1):43－48.(SHANG Xiao-san，WANG Dong.Simulation to Daily Rainfall-Runoff Process in Typical Karst Basin in Guizhou［J］.Carsologica Sinica，2009，28(1):43－48.(in Chinese))

［16］LEAHY PAUL，KIELY GER，CORCORAN GEAROID.Structural Optimisation and Input Selection of an Artificial Neural Network for River Level Prediction［J］.Journal of Hydrology ，2008，355(6):192－201.

［17］束龙仓，董贵明，陶玉飞，等.地下河天窗水位变化分析及预测［J］.水力学报，2009，40(5):529－533.(SHU Long-cang，DONG Gui-ming，TAO Yu-fei，et al.Forecast and Analysis on Water Level Fluctuation in Sinkhole of Underground Rivers［J］.Journal of Hydraulic Engineering，2009，40(5):529－533.(in Chinese))

［18］葛哲学，孙志强.神经网络理论与MATLABR2007实现［M］.北京:电子工业出版社，2007.(GE Zhe-xue，SUN Zhi-qiang.Theory of Neural Network and Its Application in MATLABR2007［M］.Beijing:Electronic Industry Press，2007.(in Chinese))

［19］武 鹏.动力电池数字终端管理系统的研究［D］.天津:天津大学，2007.(WU Peng.Study on Digital End Management System of Power Battery［D］.Tianjin:Tian-jin University，2007.(in Chinese))

［20］杨桂芳，姚长宏，王增银，等.BP神经网络在岩溶水库渗漏评价中的应用［J］.中国岩溶，2000，19(1):73－80.(YANG Gui-fang，YAO Chang-hong，WANG Zengyin，et al.Application of Back Propagation Artificial Neural Network in Leakage Evaluation for Karst Reservoirs［J］.Carsologica Sinica，2000，19(1):73－80.(in Chinese))

［21］程根伟，舒栋材.水文预报的理论与数字模型［M］.北京:中国水利水电出版社，2006.(CHENG Gen-wei，SHU Dong-cai.Theory and Digital Models of Hydrological Forecasting［M］.Beijing:China Water Power Press，2006.(in Chinese))