基于RBF多变量时间序列的滑坡位移预测研究

曾 耀，李春峰

(贵州省交通规划勘察设计研究院股份有限公司，贵阳 550001)

1 研究背景

斜坡本质上是一个受岩土体工程地质性质控制，并受地形地貌、地下水、地震和人类工程活动等多种因素影响而发展演化的开放、耗散和复杂的非线性动力学系统［1］。在上述各种因素的共同作用下，系统演化过程可视为一种具有混沌特征的动力系统［2］。滑坡是斜坡的一种成因类型，具有相同的系统特性。由于混沌系统具有内在的规律性和对初值的敏感依赖性，我们可以根据边坡变形的历史数据构成的混沌时间序列，在短期内对边坡变形破坏进行预测。

目前斜坡位移时序动态分析多采用单变量时间序列模型，即依据位移时序曲线预测滑坡的位移发展趋势，在分析斜坡的变形动态特征方面进行了有益的探索［3－4］。原则上，对自治的系统，只要嵌入维数足够大，单变量时间序列足以重构原动力系统;但在实际问题中完全不是这样，不能保证任何单变量时间序列都能重构原动力系统［5］。由于系统信息是隐含在单变量时间序列中的，不能从直观上获得系统演化的动力因素。多变量时间序列模型综合考虑几种因素，并能反映各因素间的相互关系，因此比单变量时间序列模型更能反映研究问题的实质特征。

本文结合红石包滑坡防治工程及监测成果，根据观测获得的位移及其影响因素构成多变量时间序列重构滑坡位移动力系统，采用RBF神经网络实现变量间的映射关系，进行位移预测，并初步探讨了变量的选择对模型预测效果的影响。

2 基于RBF多变量时间序列预测法

2.1 相空间重构

式中，τl，ml(l=1，2，…，M)分别表示延迟时间间隔和嵌入维数，类似于F.Takens在单变量情形下的结论。一般地，如果充分大，存在映射

也可以写成以下等价形式:

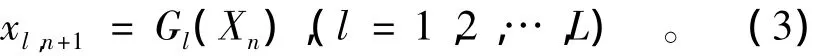
此时状态空间Xn→Xn+1的演化反映了原未知动力系统的演化，混沌时间序列预测问题就是根据一个近似形式

2.2 全局预测法

本文时间序列预测方法选择全局预测法。所谓全局预测法是将轨迹线中的所有点作为拟合对象，寻找合适的函数由于实际问题中数据总是有限的，因而不可能求出真正的Gl，只能通过有限数据构造，使

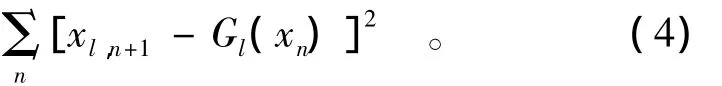
最小，从而得全局预测模型

2.3 RBF 网络结构

人工神经网络是由大量简单的神经元相连而组成的复杂系统，它不需要建立非线性动力学方程，只是依靠过去的经验去学习，通过调整人工神经网络各神经元之间的连接权，拟合系统的输入和输出，实现变量间的映射关系，而与力学系统的复杂程度无直接关系，可以很好地解决非线性演化问题。

RBF神经网络是一种具有单隐含层的3层前馈网络，由输入层到隐含层的映射是非线性的，隐含层采用径向基高斯函数作为网络的激活函数，实现从输入空间到隐含层空间的变换;网络输出和权值成线性关系，可以采用保证全局优化的线性算法;同时训练方法快速易行，不存在局部最小问题。

现以m维向量Xn输入，单输出为例构建网络。该网络的拓扑结构如图1所示。

图1 RBF网络结构图Fig.1 Structure of RBF network

在RBF神经网络结构中，网络的输入向量为m维向量Xn的转置，则网络输入层节点个数m=

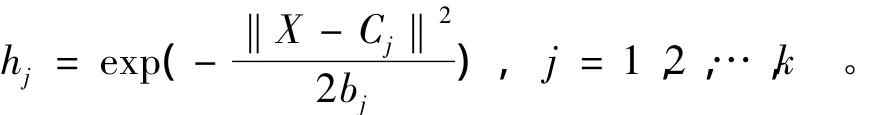
在该隐层中，第j个节点的高斯基函数中心矢量为

Cj与Xn的维数相同，可以在很大程度上决定网络性能的好坏。

设网络隐含层节点的基宽向量为

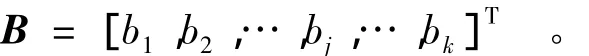
其中，bj为节点j的高斯基函数半径，其大小决定了网络的复杂程度，可以通过实验和误差信息选取适当的值;‖·‖为向量范数，一般为欧式范数。隐含层至输出层的权向量为

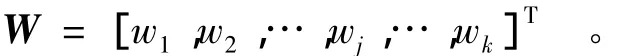
网络的输出函数为

2.4 预测效果评价

均方百分比误差MSPE越小，预测效果越好;反之预测效果越差。

3 工程实例

3.1 工程概况

红石包滑坡位于长江三峡库区巴东县城迁建新址规划区，系恩施石油总公司巴东新油库工程场地，已建成的新城区沿江大道从滑坡区前部高程181m通过。滑坡为堆积层滑坡，包括3处浅层滑坡和1个浅层变形体，以及1个规模较大的深层潜在滑移带，边坡平均坡度约25°，现由于新建油库，使滑坡地貌大为改观，形成5级平台。滑坡治理工程于2002年10月21日竣工。对红石包滑坡的治理，主要采用锚拉桩与悬臂桩联合方案，外加削坡减载(土石方)、挡土墙、护坡、排水沟工程，构成红石包滑坡治理的总体实施方案，以确保滑坡的整体与局部稳定。为了解新油库区滑坡体的安全稳定及验证滑坡治理效果，尤其是三峡库区蓄水后对滑坡体稳定性的影响，确保油库安全，于2002年10月开始了滑坡水平位移监测、渗透水压力监测和抗滑桩钢筋应力监测等监测项目。

3.2 预测模型建立

滑坡位移是滑坡状态的直接反映，滑坡位移主要外在动力因素为地下水，滑坡治理后抗滑桩是滑坡位移的主要阻滑因素，此时滑坡在这些影响因素的综合影响下演化。在实际监测中常以渗透水压力来表征地下水对滑坡的影响，以抗滑桩钢筋应力来表征抗滑桩工作状态。

目前较常用做法是建立位移单变量时间序列，利用位移历史数据预测位移。本文重点讨论位移及其影响因素构成的多变量时间序列的预测位移。

3.2.1 监测数据

监测数据的时间区间为2003年8月至2007年8月，由于监测数据间隔时间不大，经过线性内插处理得48组时间序列，时间间隔为1个月。H04为位移监测点，P02为渗透水压力监测点，R02为抗滑桩北侧中央主筋应力监测点，R04，R06，R07为抗滑桩南侧中央主筋应力监测点。具体监测值数据见表1。

由监测数据分别得P02，R02，R04，R06，R07，H04监测点监测值的时间序列为

现以H04监测点岩体内部水平位移预测为例建立预测模型，选取前43组数据进行相空间重构，后5组数据为预测集。

3.2.2 预测模型

3.2.2.1 单变量时间序列预测模型

由(1)式可得如下重构相空间:

则单变量位移时间序列全局预测模型为

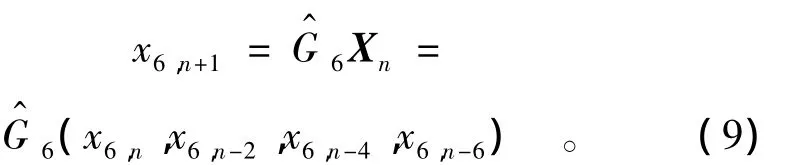
可得36组训练样本，5组预测集。RBF神经网的输入节点数即为空间维数m=ml=4，输出节点数为1。

3.2.2.2 多变量时间序列预测模型

本文采用分别求取各个单变量时间序列的时间延迟和嵌入维数的方法对滑坡位移动力系统进行相空间重构。求取方法同上，具体值见表2。

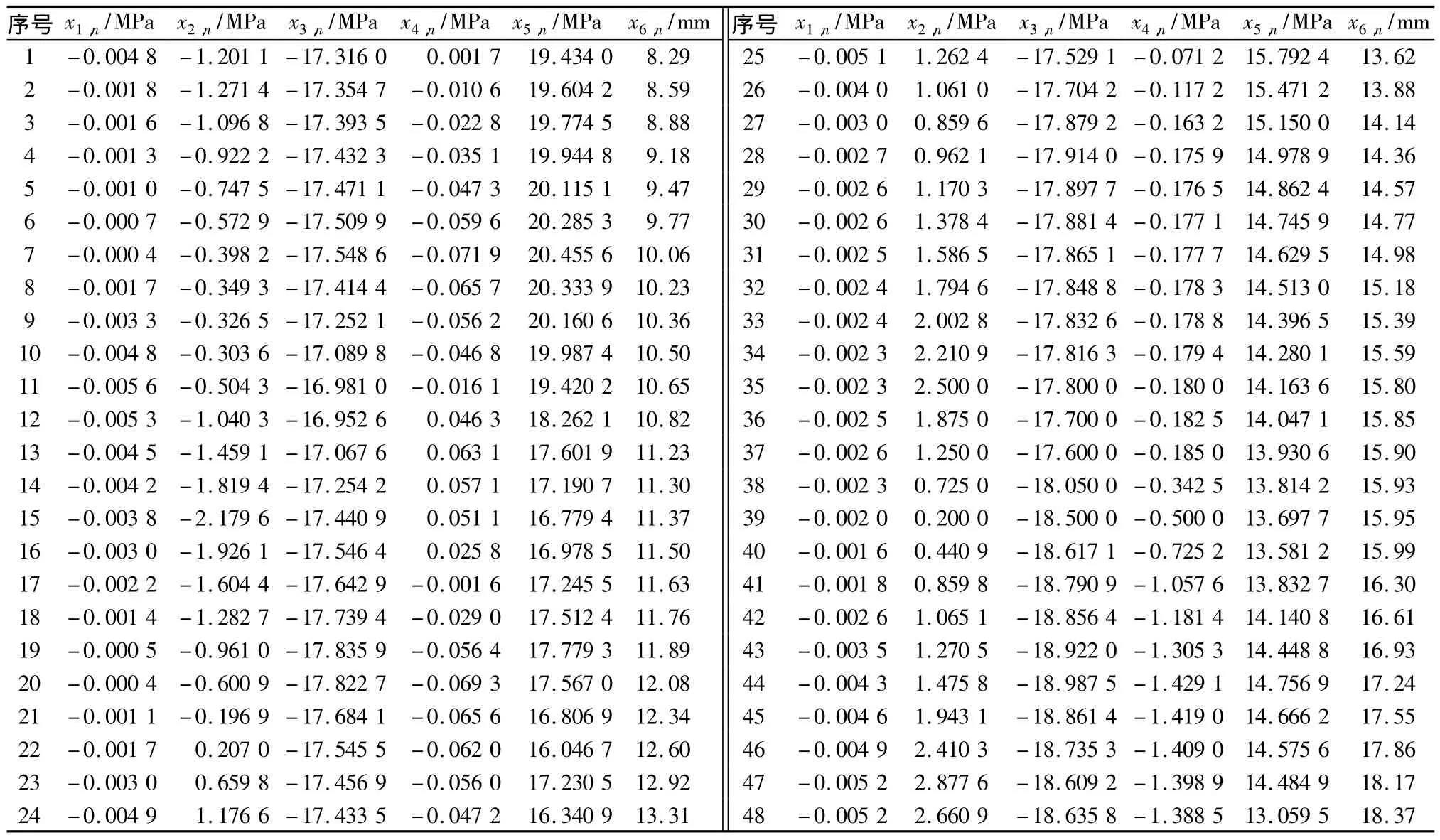
表1 红石包滑坡位移预测模型输入、输出数据Table 1 Input and output data of the prediction model for Hongshibao landslide

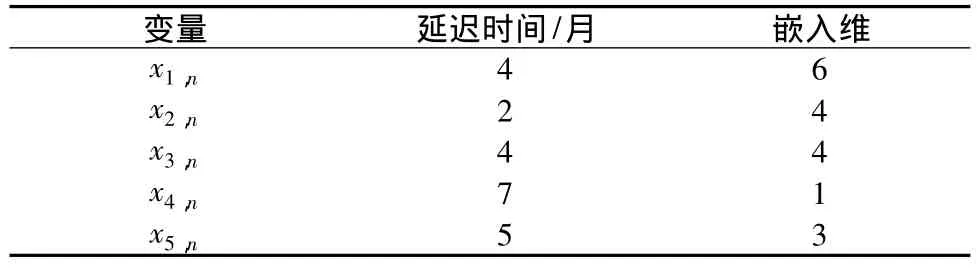
表2 相空间重构参数表Table 2 Parameters of phase space reconstruction

为考虑影响因素对预测效果影响分别按如下3种方式进行相空间重构，重构变量选取如下:

① 考虑渗透水压力影响:x1，n，x6，n;

③同时考虑渗透水压力及抗滑桩影响:x1，n，

分别按式(1)式进行相空间重构。现以多变量①组合为例建立多变量预测模型。

则多变量位移时间序列全局预测模型为

可得22组训练样本，5组预测集，RBF神经网的输入节点数为10，输出节点数为1。

同理可建立多变量②、③组合的预测模型。其中多变量②组合情况下空间维数为14，可得训练样本30组;多变量③组合情况下空间维数为22，可得训练样本22组。预测集均为5组，输入节点数均为1。

3.3 预测结果

为避免输入向量物理意义和单位的不同对RBF神经网络建模的影响，对输入向量需作归一化处理，目的是为了消除数量级大小不同的影响，使其变成相同数量级，以防某些数值低的特征被淹没。对于向量X，归一化公式为

式中:x'为x标准化处理过的向量;xmin，xmax为向量X中的最小值和最大值。

RBF神经网络能以任意精度逼近复杂函数，为防止过拟合现象的出现，训练误差不宜取得过低，同时应选择合适的基宽，在Matlab中为选择合适的扩展常数。

计算结果详见表3。由表3预测结果可看出:多变量时间序列预测模型预测精度均较单变量时间序列预测模型高;在分别考渗透水压力及抗滑桩影响时预测精度比较接近;在同时考虑两者影响时预测精度有所提高，此时MSPE为0.001 1，较单变量预测效果有较大幅度提高。出现上述现象的原因是多变量时间序列包含有比单变量时间序列关于滑坡位移动力系统的更为丰富的信息，同时选择合理的多变量组合能更有效地重构原动力系统、反映其演化特征。

另外结合表1可看出随着时间推移:H04点位移逐渐增大，R02点北侧中央主筋由压应力逐渐向拉压力状态转变，R04和R06处于压应力状态且压应力逐渐增大，R07处于拉压应力状态且向压应力状态转变。P02点渗透水压力受降雨影响处于缓慢波动状态。多变量预测模型反映了滑坡位移与其影响因素的相关性:滑坡在地下水渗流作用下稳定性降低、位移逐渐增大，而这种趋势受到抗滑桩的限制。尤其在多变量③综合考虑各种影响因素的情况下能够较全面地反映滑坡位移动力系统信息。

4 结论

滑坡作为斜坡的一种成因类型，其发展演化具有混沌特征。位移作为其发展演化状态的宏观表现，其预测具有明显的不确定性，但可以通过观测所得的位移及其影响因素的多变量时间序列重构原滑坡位移动力学系统，并对其位移进行短期预测。结合具体工程实例，研究表明:

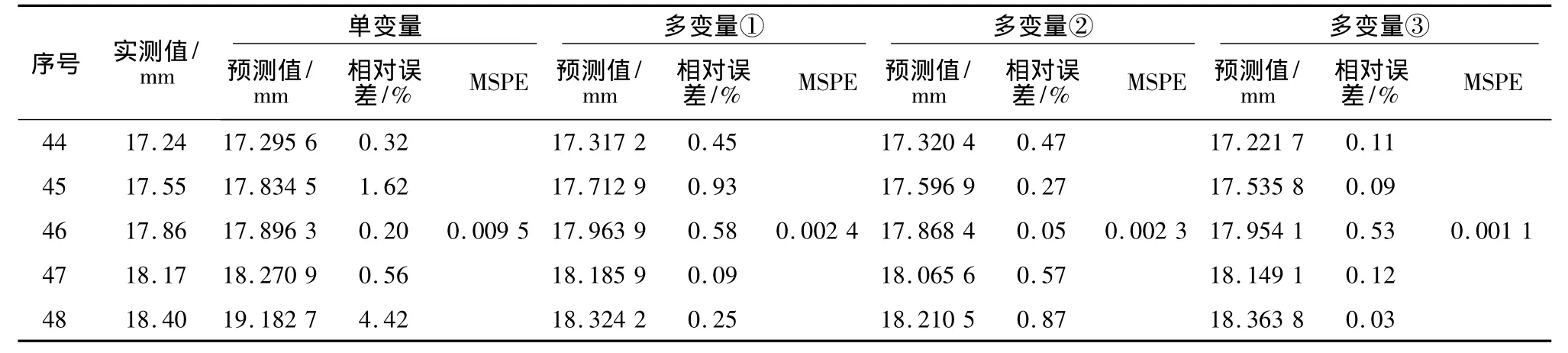
表3 红石包滑坡位移预测计算成果Table 3 Calculation results of the displacement prediction for Hongshibao landslide

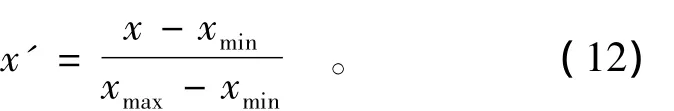
(1)多变量时间序列包含有比单变量时间序列关于滑坡位移动力系统的更为丰富的信息，采用多变量时间序列模型的预测精度较单变量时间序列预测模型高，能够取得较好的预测效果。

(2)多变量预测模型反映了滑坡位移与其影响因素的相关性，因此具有更明确的物理力学意义，更能反映反映滑坡演化变形的实质特征。

致谢:本文工程实例来源于中国水利水电科学研究院提供的《湖北巴东新油库区红石包滑坡2004—2007年度安全监测报告》，特此向中国水利水电科学研究院及相关研究人员表示感谢!

［1］付义祥，刘志强.边坡位移的混沌时间序列分析方法及应用研究［J］.武汉理工大学学报(交通科学与工程版)，2003，27(4):473－476.(FU Yi-xiang，LIU Zhiqiang.Analytic Method and Application about Chaotic Slope Deformation Destruction Time-series［J］.Journal of Wuhan University of Technology(Transportation Science and Engineering)，2003，27(4):473－476.(in Chinese))

［2］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2002.(LV Jin-hu，LU Jun-an，CHEN Shi-hua.Analysis and Application of Chaotic Time-series［M］.Wuhan:Wuhan University Press，2002.(in Chinese))

［3］刘勇健，张伯友.混沌时间序列在边坡位移预测中的应用［J］.辽宁工程技术大学学报，2007，26(1):74－76.(LIU Yong-jian，ZHANG Bo-you.Application of Chaotic Time-series in Slope Displacement Forecasting［J］.Journal of Liaoning Technical University，2007，26(1):74－76.(in Chinese))

［4］刘 晓，曾祥虎，刘春宇.边坡非线性位移的神经网络-时间序列分［J］.岩石力学与工程学报，2005，24(19):3500－3504.(LIU Xiao，ZENG Xiang-hu，LIU Chun-yu.Research on Artificial Neural Network Time Series Analysis of Slope Nonlinear Displacement［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(19):3500－3504.(in Chinese))

［5］王海燕，卢 山.非线性时间序列分析及其应用［M］.北京:科学出版社，2006.(WANG Hai-yan，LU shan.Nonlinear Time Series Analysis and Its Application［M］.Beijing:Science Press，2006.(in Chinese))

［6］FRASER A M.Information and Entropy in Strange Attractors［J］.IEEE Transactions on IT，1989，35(2):245－262.

［7］CAO L Y，MEESA，JUDD K.Dynamics from Multivariate Time Series［J］.Physica D，1998，121:75－88.