松江河梯级水电站短期优化调度数学模型分析

冯雁敏，张雪源，梁年生

(1.东北电力科学研究院有限公司，沈阳 110006;2.东北电网有限公司，沈阳 110180;3.华中科技大学，武汉 430074)

1 研究背景

松江河发电厂有4座水库、3个电站、6台水轮发电机组，各水库调节性能不同，各电站区间来水复杂，电站间水头、流量联系紧密，各电站间水轮发电机组的型号及其动力特性不同，对运行方式的制约因素很多，难以根据调度管理人员的经验找到最优运行方案。各电站间既存在着电力方面的联系，又存在着水利、水力方面的联系，上级电站发电用水和弃水经过一定时间流达下游水库，将会影响下级各电站的发电，而下级电站的水库调节能力又反过来影响上级电站的用水计划［1－3］。梯级电站短期优化调度是一个强约束、非线性、多变量、多阶段的大规模优化问题，其求解过程非常复杂。本文建立梯级电站发电量最大和发电效益最大2种数学模型，并将2种优化结果进行分析比较。

粒子群算法(Particle Swarm Optimization，PSO)是Kennedy博士和Eberhart教授于1995年提出的一种基于群体智能的仿生类随机全局优化方法，该算法具有流程简单、计算参数少、收敛速度快、鲁棒性强等优点，适合求解梯级电站短期优化调度问题，但PSO存在2个主要缺陷:一是后期收敛速度慢，在较大的惯性系数作用下，粒子运动将远离最优解;二是种群多样性丧失较快，易陷入局部最优解而发生“早熟”现象。本文通过引入收缩因子和基于遗传思想的变异算子对其进行改进，并应用其求解梯级电站短期优化调度问题［4－7］。

2 松江河梯级水电站概况

松江河梯级水电站位于头道松花江上游支流松江河和漫江上，由松山引水工程和小山、双沟、石龙3座水电站组成，其工程特性参数如表1所示。梯级电站以发电为主，总装机容量为510 MW。由于石龙水库调节性能较差，使梯级电站机组过流能力不匹配，导致石龙电站运行方式受到限制，应与双沟电站联合调度，合理安排开停机顺序。

表1 松江河梯级水电站工程特性Table 1 The main parameters of Songjianghe cascade hydropower stations

3 梯级电站短期优化调度数学模型的建立

3.1 梯级电站短期优化调度数学模型

水电站的运行方式主要取决于其天然来水情况，在其运行方式变动对电网运行影响很小时，水电站可按自身最有利的方式运行，如在满足日用水量要求和各种限制条件下使日发电量(或日发电收益)最大。松江河梯级电站自上而下为松山水库、小山电站、双沟电站、石龙电站，将水库编号为i=1，2，3，…，I。I为水库总数。将一个计划日分成T个时段，t为时段顺序编号，ΔT为时段间隔。日发电量最大和日发电效益最大目标函数如式(1)、(2)示:

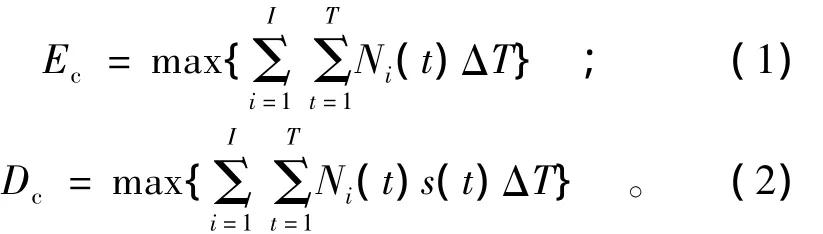
第i电站在t时段的出力计算式为

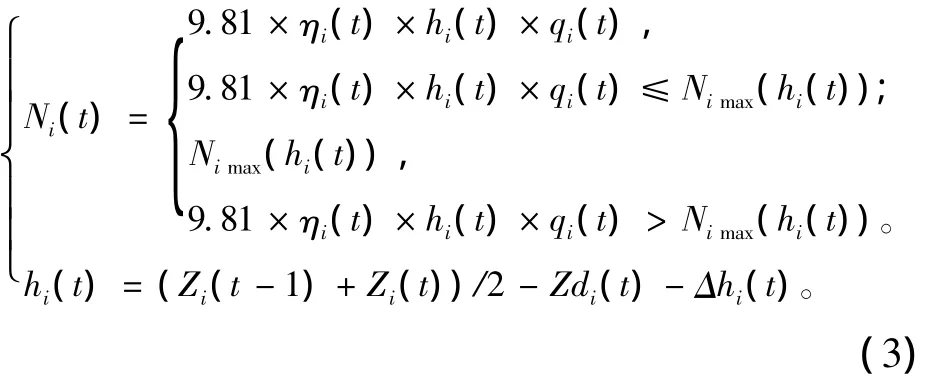
式中:Ec为梯级电站日最大发电量;Ni(t)为第i电站在第t时段出力;Dc为梯级电站日最大收益;s(t)为第t时段电价;ηi为第i电站在t时段的水轮发电机组效率;hi(t)为第i电站在t时段的工作水头;qi(t)为第i电站在t时段的发电流量;Nimax(hi(t))为第i电站在对应水头的最大限制出力;Zi(t－1)，Zi(t)分别为第i电站在第t时段初、末库水位;Zdi(t)为第i电站在t时段的下游水位;Δhi(t)为第i电站在t时段的水头损失。

3.2 约束条件

梯级电站短期优化调度主要约束条件如下。

(1)水量约束:

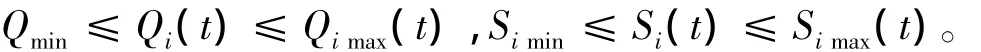
(2)水量平衡方程:

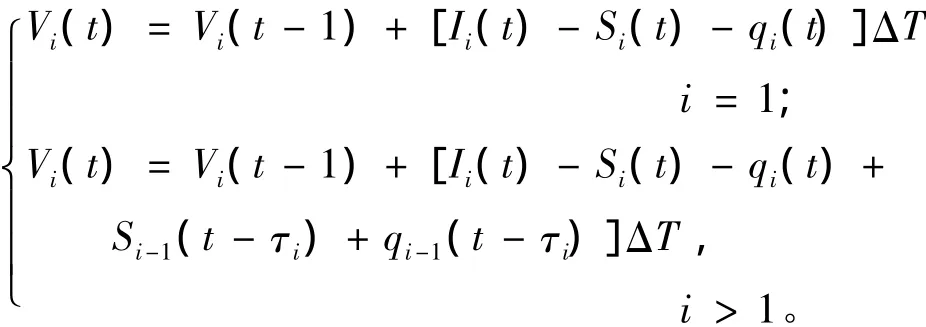
(3)水位约束:

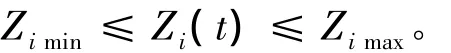
(4)出力约束:

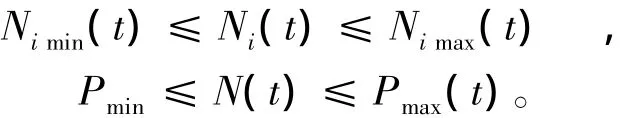
(5)其它约束:如机组完好状态约束、避开水电机组强振区等。

式中:Qi(t)为第i电站第t时段的引用水量(包括发电流量和弃水流量);Ii(t)为水库i在时段t内的自然入库流量;Si(t)为水库i在时段t内的弃水流量;τi为第i－1水库水流流至第i水库所需时间，即水流时滞;Zi(t)为第i电站在第t时段末的库水位;Zimin(t)，Zimax(t)为第i电站在第t时段的最小、最大库水位限制;Nimin(t)，Nimax(t)为第i电站在第t时段的最小、最大出力限制;N(t)为第t时段梯级电站的总出力;Pmin(t)，Pmax(t)为第t时段电力系统对梯级电站总出力最小、最大需求限制;Qimin(t)，Qimax(t)为第i电站在第t时段最小、最大引用流量限制;Simin(t)，Simax(t)为第i电站在第t时段最小、最大弃水流量限制。

4 粒子群算法及其改进

4.1 粒子群算法的基本原理

应用PSO求解优化问题时，问题的每个解对应于一个粒子，每个粒子都有自己的位置和速度，还有一个由被优化函数决定的适应值。每个粒子利用自身的记忆和从群体中获得的信息更新自己的速度矢量和位置以追随当前的2个“极值”，并通过群体中的信息共享来实现寻优搜索。这2个极值包括个体极值和全局极值，粒子本身所找到的最优解，叫做个体极值，整个种群目前找到的最优解，叫做全局极值。其计算流程如下:首先，在可行解内随机初始化一定数量的粒子;然后，计算各个粒子的适应值、个体极值及全局极值，粒子可根据式(4)来更新自己的位置和速度，直到找到最优解，迭代终止。算法迭代终止条件一般为达到最大迭代次数或搜索到的最优位置的适应值满足预定的最小适应度阈值。

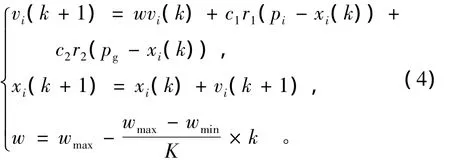
式中:vi(k)，vi(k+1)分别是第i个粒子在第k，k+1步迭代时的速度;xi(k)，xi(k+1)分别是第i个粒子在第k，k+1步迭代时的位置;pi为个体极值，表示第i个粒子经历过的最好位置;pg为全局极值，表示所有粒子所经历过的最好位置;c1，c2是常数，0＜c1＜c2＜2［4］;r1，r2是［0，1］区间均匀分布的随机数;权重系数w随算法迭代的进行而线性地减少为算法的总迭代次数。

4.2 改进粒子群算法

PSO在求解优化问题时存在粒子种群多样性丧失迅速，难以收敛于全局最优等缺点。引入收缩因子χ和自适应变异算子对PSO进行改进［4－7］。

4.2.1 引入收缩因子

权重系数w对优化性能有很大的影响，w较大时算法具有较强的全局搜索能力，w较小时算法有利于局部搜索。w线性递减只对某些问题有效，但对于不同的问题，其每次迭代所需要的比例关系并不相同，为此，引入收缩因子。该方法描述了一种选择w，c1，c2值的方法，以确保算法收敛。通过正确选择这些控制参数，就不必将 vi，j限制在［－vmax，vmax］中。带有收缩因子的运动方程式如式(5)示:

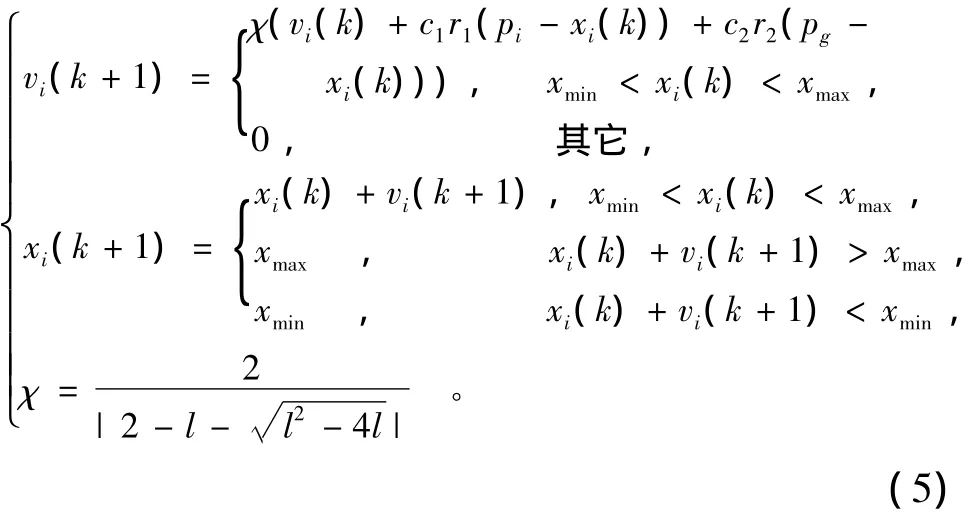
式中:c1=2.8，c2=1.3，l=c1+c2;微粒群规模 N=30;χ为收缩因子，其作用类似于参数vmax的作用。试验结果表明，与vmax和w相比，χ更能有效地控制粒子的变化速度，具有更好的收敛性［4－5］。

4.2.2 引入变异算子

为克服PSO难以收敛于全局最优解的缺陷，在每个迭代阶段内选择一半粒子群进行变异，以防止算法陷入局部最优。变异方法如下:首先以适应值为判断依据，对种群中所有个体进行由优到劣排序，选择种群底部的一半个体作为被变异的粒子。然后对种群中顶部的一半个体进行基于遗传思想的变异复制，并取代被变异的粒子，在此过程中全局极值并未改变。粒子变异运动方程如式(6)示

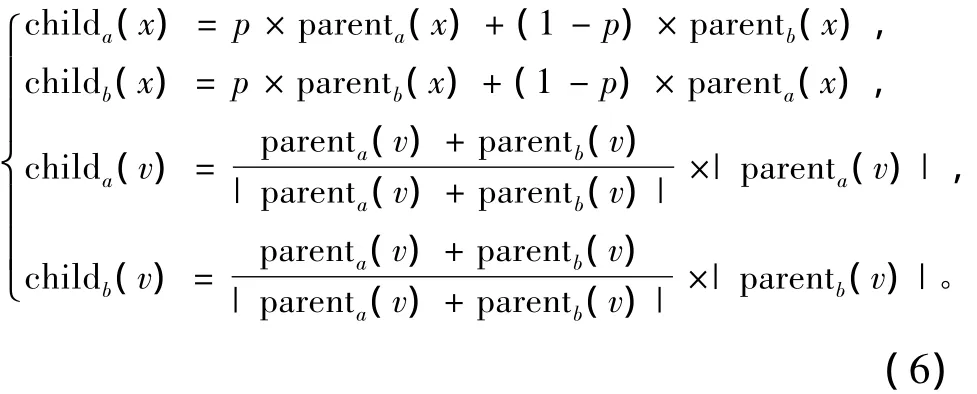
式中:x是D维位置向量元素;p是D维均匀分布的随机数向量元素，其每个分量都在［0，1］内取值;v为D维速度向量元素。经过任意2个亲代个体的杂交操作，随机产生了2个新的位置，速率的交叉处将2个亲代个体的速率之和的长度规格化，只有方向受到影响，数量没有被影响，交叉操作继承了双亲粒子的优点，加强了跳出局部最优的能力［4］。

5 算例分析

5.1 基础数据

已有松江河各电站机组完好状态、机组及电站动力特性数据、机组稳定性特性数据、各水库库容特性曲线、下游水位与流量关系曲线;已知计划日的各水库库水位、水库来水、电站区间来水、各电站实际运行数据及对电站运行方式的限制因素等。各电站优调方案的日初、末库水位与实际运行相同，即日用水量相同。计划日梯级电站模拟交易电价如图1所示。

图1 计划日梯级水电站电价模拟图Fig.1 Simulation of electricity price of cascade hydropower stations on scheming day

说明:当P≤0.85Pmax时，为低谷负荷和基荷，其电价定为0.05元/kW·h;当0.85Pmax＜P≤0.9Pmax时，为腰荷，其电价定为0.10元/kW·h;当0.9Pmax＜P≤0.94Pmax时，为腰荷，其电价定为0.15元/kW·h;当P ＞0.94Pmax时，为峰荷，其电价定为0.25元/kW·h。P为实时负荷，Pmax为最大负荷。

5.2 求解方法

应用改进粒子群算法求解该问题可表述为:找到一个最优粒子，即一种最优调度策略(各水库水位Zi(t)的最优变化序列)，在满足电网、水库、电站及机组的多种约束条件下使梯级电站发电量(或发电效益)最大。求解步骤如下:

(1)设置粒子群规模(N=30)，初始化各粒子，确定各类限制条件和迭代终止判据。

(2)计算所有粒子的适应值，将各粒子的适应值暂时作为各粒子的个体极值，所有个体极值中最好的粒子作为全局极值。

(3)根据引入收缩因子的运动方程更新各个粒子的位置和速度。

(4)计算更新后各粒子的适应值，若更新后粒子的适应值优于该粒子当前个体极值或全局极值，则将更新的粒子作为该粒子的个体极值或全局极值。

(5)根据适应值优劣排序，引入变异算子进行交叉计算。

(6)检验是否满足迭代终止条件，若满足则迭代终止、输出结果，否则转到(4)继续迭代，至到迭代终止。全局极值的位置即为梯级电站的最优调度参数。

5.3 计算结果及分析

5.3.1 日发电量最大方案

以日发电量最大为优化准则，计算在日用水量给定条件下的松江河梯级电站最优日运行方式，对30 d的运行数据进行优化计算，计算成果见表2。

通过分析可得出以下结论:①与实际运行方案相比，优调方案日发电量可增加2.88%～6.95%，在仿真计算的30 d中，共增发电量993.49万kW·h，效益可观;②优调方案具有先蓄水后发电的规律，计划日初尽量少发电，将规定的日用水量放在接近日末的时段中用，可使水量在尽可能高的水头下发电，优调方案符合直观分析规律;③在某些天内石龙电站优调方案的发电量比实际发电量小，但梯级电站总发电量增加了，说明总体(水电站群)最优和局部(单个电站)最优并不完全一致;④在优调方案中存在石龙电站经常在日初第1时段发电，而双沟电站在此时段及其后多个时段都不发电的＇怪现象＇。这是由于石龙电站为提高运行水头，库水位一直保持在正常最高值，虽然上库无下泄流量，但还有区间流量入库，在日初用发电方式按区间来水量大小腾空水库，避免弃水，以增加发电量。

5.3.2 日发电效益最大方案

以日发电效益最大为优化准则，计算在日用水量给定条件下松江河梯级电站的最优日运行方式，对30 d的运行数据进行优化计算，计算成果见表3。

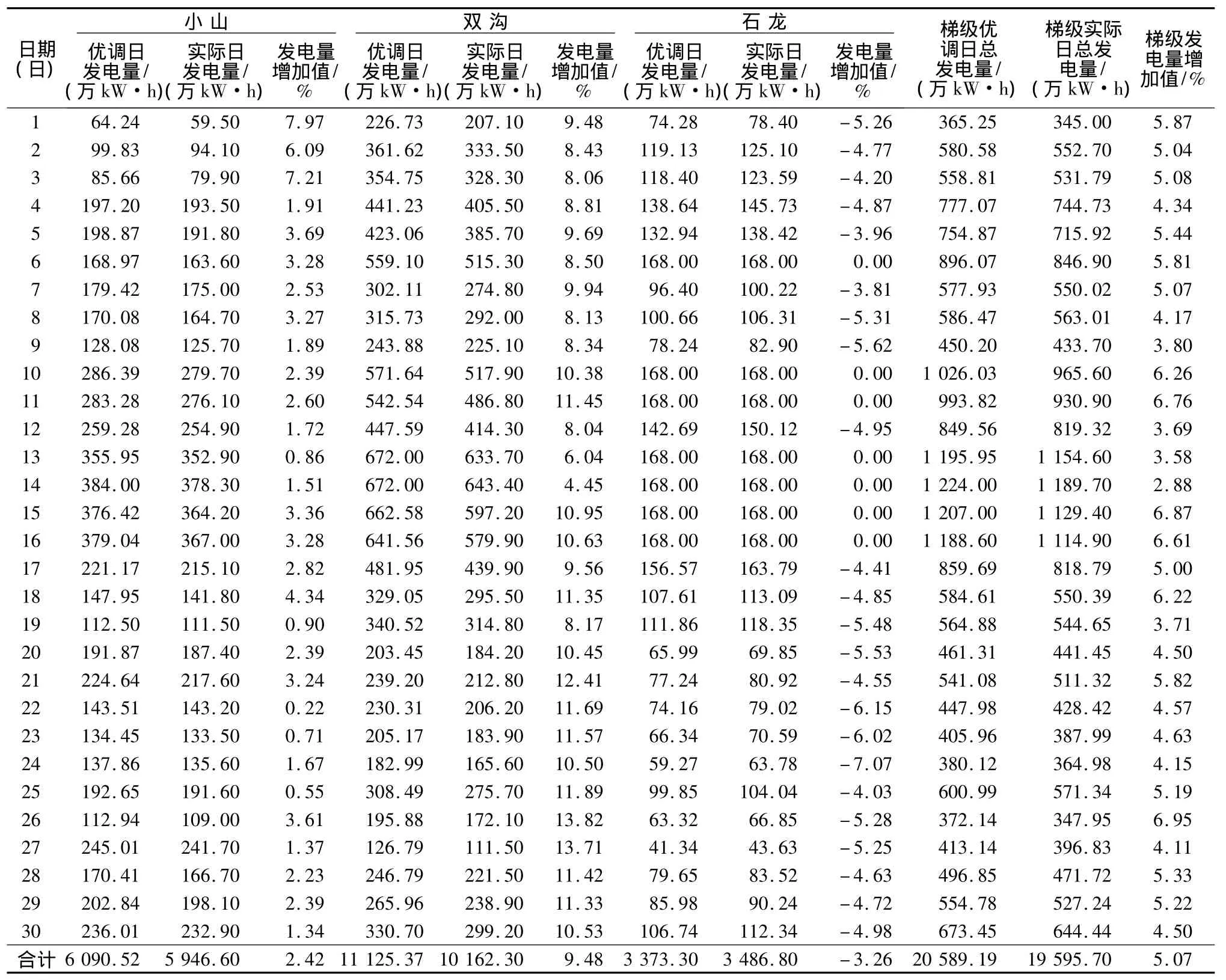
表2 松江河梯级电站发电量最大方案仿真计算成果Table 2 Optimal results of Songjianghe cascade hydropower stations calculated by maximizing power generation

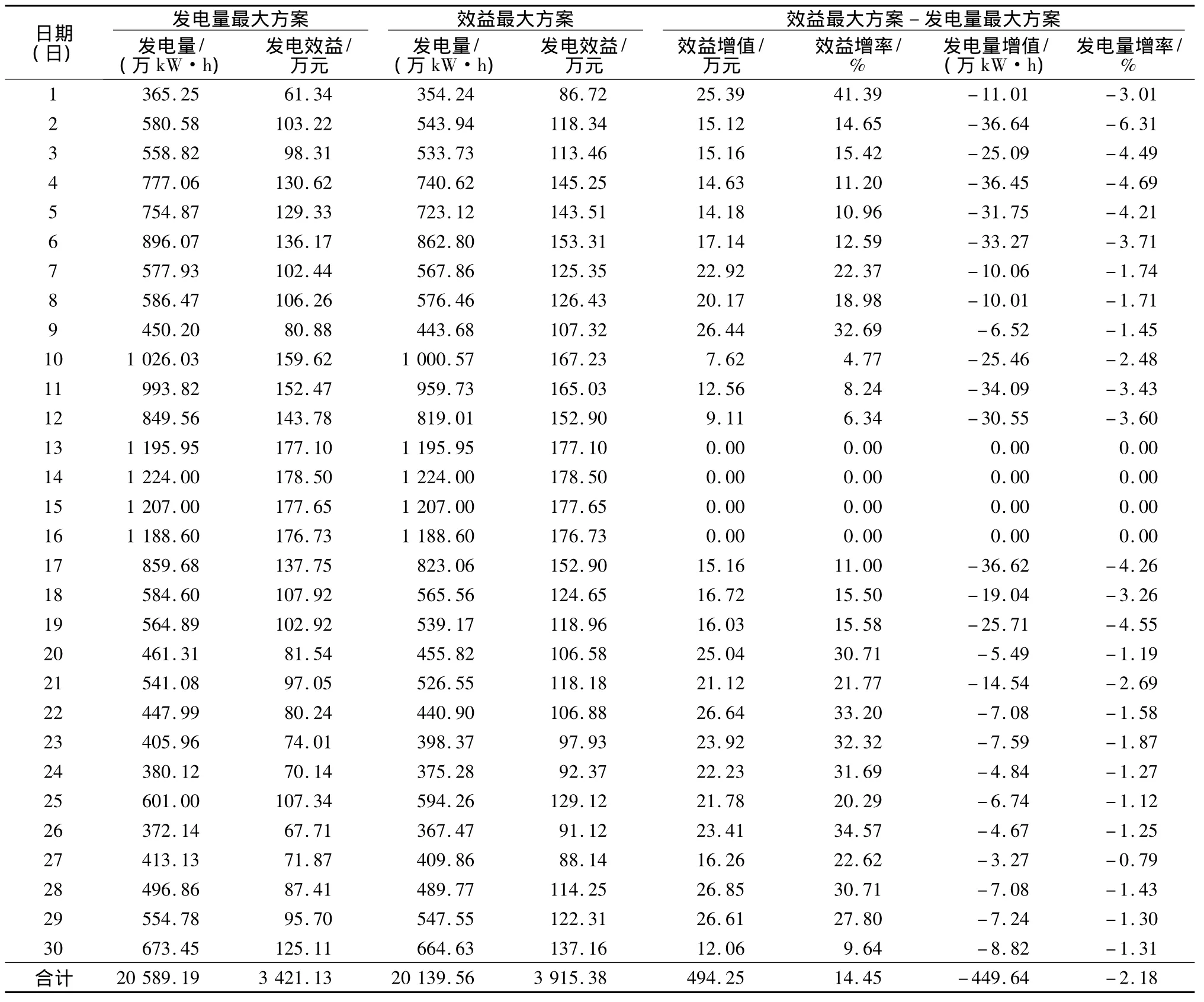
表3 松江河梯级电站发电效益最大方案仿真计算成果Table 3 Optimal results of Songjianghe cascade hydropower stations calculated by maximizing generation profit

通过分析可得出以下结论:①与发电量最大调度方案相比，经济效益最大调度方案日均发电量减少14.99万kW·h，但日均经济收入增加16.48万元，该方案除充分利用水头增加发电量外，还考虑各时段间的电价差异，尽可能大地增加经济收益。当用水量充裕时，可全时段以装机容量发电，此时，这2种优化方案相同。②在日优调方案中，石龙电站存在在日初时段(低电价区)发电现象。虽然此时双沟电站无下泄流量，但有区间入库流量，石龙水库日初已蓄满，若不发电将弃水。但计划日区间来水很小，只用本时段不蓄水量无法发电，故将水库进行发电预泄，待蓄未来时段的区间入库流量至双沟电站开始发电下泄流量到达石龙水库前蓄到期望水位。若区间来水较大，可将石龙水库维持在高水位，直至双沟电站开始发电下泄流量到达石龙水库前才加大出力，迅速降至期望水位。③此次计算，发电量最大和经济效益最大这2种优调方案比实际日发电量分别增加33.12万kW·h和18.13万kW·h，对梯级水电站进行短期优化调度可提高其整体质量和效益。

6 结论

随着松江河梯级调度中心的逐渐形成和完善，研究松江河梯级水电站短期优化调度问题，对于把握梯级水电站的运行规律，提高梯级电站的整体质量和效益有重要意义。本文建立了发电量最大和发电效益最大梯级电站短期优化调度数学模型，并应用改进粒子群算法求解松江河梯级电站短期优化调度问题，对梯级水电站进行短期优化调度可以提高水能利用率及整个梯级电站的经济效益。应用改进粒子群算法求解梯级水电站短期优化调度问题，无论求解精度、求解时间还是求解结果的合理性都取到了较满意的结果。

［1］张高峰，权先璋，余 波，等.三峡梯级日优化运行模型及算法［J］.长江科学院院报，2003，20(3):10－12.(ZHANG Gao-feng，QUAN Xiang-zhang，YU Bo，et al.Optimal Daily Operation Model and Algorithm for Three Gorges Cascade Hydropower Plants［J］.Journal of Yangtze River Scientific Research Institute，2003，20(3):10－12.(in Chinese))

［2］吴杰康，郭壮志，秦砺寒，等.基于连续线性规划的梯级水电站优化调度［J］.电网技术，2009，33(8):24－29.(WU Jie-kang，GUOZhuang-zhi，QIN Li-han，et al.Successive Linear Programming Based Optimal Scheduling of Cascade Hydropower Station［J］.Power System Technology，2009，33(8):24－29.(in Chinese))

［3］谢红胜，吴相林，陈 阳，等.梯级水电站短期优化调度研究［J］.水力发电学报，2008，27(6):1－7.(XIE Hong-sheng，WU Xiang-lin，CHEN Yang，et al.Research on Short-term Optimization Operation of Cascade Hydropower Stations［J］.Journal of Hydroelectric Engineering，2008，27(6):1－7.(in Chinese))

［4］SUGANTHANPN.Particle Swarm Optimizer with Neighborhood Operator［C］∥Proceedings of the Congress on Evolutionary Computation.Washington D.C，July 06－09，1999.

［5］杨 维，李歧强.粒子群优化算法综述［J］.中国工程科学，2004，6(5):87－94.(YANG Wei，LI Qi-qiang.Survey on Particle Swarm Optimization Algorithm［J］.Engineering Science，2004，6(5):87－94.(in Chinese))

［6］KENNEDY J，EBERHART R.Particle Swarm Optimization［C］∥Proceedings of the IEEE International Conference on Neural Networks.Perth，Australia.Nov.27－Dec.01，1995，4:1942－1948.

［7］冯雁敏，李承军，张雪源.基于改进粒子群算法梯级水电站短期优化调度研究［J］.水力发电，2009，35(4):24－28.(FENG Yan-min，LI Cheng-jun，ZHANG Xueyuan.Research on the Short-term Optimal Scheduling of Cascade Hydropower Plants Based on Improved Particle Swarm Optimization［J］.Water Power，2009，35(4):24－28.(in Chinese))