变分法在大学数学研究性教学中的探讨

刘艳芹

（德州学院，山东 德州 253023）

变分法是一种研究泛函极值的经典方法。变分的理论和方法不仅在数学的很多分支中，而且在工程技术等众多领域中都有着广泛的应用。变分法涉及到泛函分析的知识，一般情况下学生感觉内容晦涩难懂且不易理解，这也是困扰教师教学的一个问题。在当今大学提倡研究型教学，以培养研究型人才为目标的形式下，教师在讲授变分的理论和方法的同时，让学生接触一些变分法在不同的物理背景以及后续可研究工作中的应用等问题，即教学和科研相结合是值得研究和探讨的问题。在保证教学质量的前提下，突出学科的科研优势是我们追求的目标。在变分法的教学过程中结合教学经验以及科研工作的体会，从教学内容、教学方法以及研究性应用等方面提出几点教学改革探讨。

一、教学内容方法的创新

在变分学的理论研究和实际应用中，都必须具备一定的数学基础知识。如微积分、常微分方程等是非常重要的工具［1］。我们希望教学和科研联系在一起，教师将后续科研问题及时地融入到教学过程中，不断地更新教学内容，培养学生的创新能力和激发学生的学习兴趣，使学生了解到更多的信息和掌握解决问题的技巧。

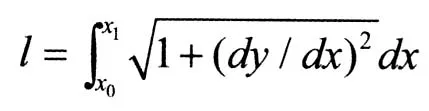
二、变分法的研究性应用

变分法的提出不但解决了最速降线问题、悬链线问题和等周问题等一系列的数学难题，还在弹性力学、流体力学、量子力学和工程技术等众多领域有着广泛的应用，目前仍有很多的科学工作者致力于变分法的研究。

（一）欧拉方程的应用

欧拉方程在求解泛函极值问题中起到了非常重要的作用，至今是研究各类问题的有效方法。教师在教学中可适当将最新的前沿知识渗透给学生，如2011年有作者在《低温建筑技术》发表《利用经典变分法对最小旋转曲面问题解答》一文［2］，该文主要就是利用变分法经典欧拉方程和传统做法中欧拉方程的初积分方程分别对最小旋转曲面问题进行了解答，教师可用此文引导学生思考，即使是经典的知识也可有创新的地方，也可让学生试着用这种思路去考虑最速降线等其他的问题，从而加深他们对变分法理论知识和应用的理解，提高解决实际问题的能力。

教师丰富的知识体系能使学生体会到学科之间的联系，任何一门知识都不是孤立存在的，它往往与很多学科领域有着相关性。希望学生能够从整体上把握知识结构，形成体系，为今后的工作和科研打下坚实的基础，这也是我们研究性的教学过程中一直探讨的问题。

（二）求解非线性问题的应用

结合自己的科研体会，给出变分法在求解非线性问题中的一点应用。研究非线性常、偏微分方程（组）的精确解和近似解是一项非常有价值和重要意义的工作。

考虑如下Fisher型的非线性单种群扩散问题

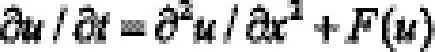
其中u（x，t）表示种群的密度，反应项F（u）是种群的增长项，初值条件：u（x，0）=1/（1+ex）2，根据变分迭代法的思想［3］建立如下的迭代关系式：

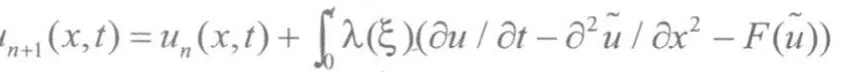
u0（x，t）表示初始近似值，λ（ξ）是Lagrange乘子，即所谓的变分，令广义泛函取极值，注意到，有

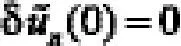
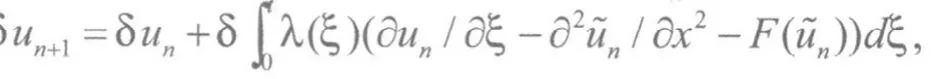
取极值的必要条件为：

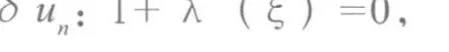
得Lagrange乘子λ（ξ）=-1，利用迭代关系式和初值条件进行迭代便得到问题的近似解。变分迭代法求解非线性问题是当今一个非常热的研究课题。

在保证教学大纲的教学内容得以实现的前提下，教师根据学生已经掌握的基础知识，做好前期辅导工作，自然地引入研究性的教学内容，并合理的安排教学时间，引导学生课下思考和探究问题，开拓锻炼学生思考问题的能力［4］。

三、注重数学思想，培养学生素质

1696年Johann Bernoulli提出的“最速降线”问题是向数学家提出的一个难题。Hospital，Leibniz，Newton都得到了解答，直到后来的Euler和Lagrange发明了这一类变分问题的普遍解法，建立了数学的一个新分支—变分学。我国著名的科学家、教育家钱伟长院士从最小位能原理出发将约束条件利用Lagrange乘子引入到泛函中，得到了广义的变分原理。钱院士在弹性力学、摄动方法和变分原理等方面都有着重要的成就，钱老也致力于当代大学生的教育问题。教师在讲授变分法的同时，可以不断地渗透大师们的研究成果和数学史的介绍，给予学生数学思想方法和精神实质的启迪，避免数学教学过程的枯燥乏味，对学生数学文化的熏陶和数学素养的形成和提高都有着极其重要的作用。

［1］ 东北师范大学数学系.常微分方程［M］.北京：高等教育出版社，2001.

［2］ 何东坡，冯宁.关利用经典变分法对最小旋转曲面问题解答［J］.低温建筑技术，2011，（3）：46-47.

［3］ Odibat A M.Construction of solitary solutions for nonlinear dispersive equations by variational iteration method［J］.Physics Letters A，2008，372（2）：4045-4052.

［4］ 董立华，于波.关于大学教师进行研究性教学的探讨［J］.高等理科教育，2010，（4）：24-27.