改进的时变非线性负荷预测组合算法
2012-11-09陈锦攀罗滇生肖时勇
陈锦攀, 罗滇生, 周 勇, 贺 辉, 肖时勇
(1.湖南大学电气与信息工程学院, 长沙 410082;2.湖南省电力公司调度通信局, 长沙 410007;3.湖南省电力公司娄底电业局, 娄底 417000)
改进的时变非线性负荷预测组合算法
陈锦攀1, 罗滇生1, 周 勇2, 贺 辉2, 肖时勇3
(1.湖南大学电气与信息工程学院, 长沙 410082;2.湖南省电力公司调度通信局, 长沙 410007;3.湖南省电力公司娄底电业局, 娄底 417000)
为了提高超短期负荷预测精度,提出了一种改进的基于学习的时变非线性组合预测算法,该算法在基预测器中增加了基于最大Lyapunov指数的混沌时间序列预测模型,其中最大Lyapunov指数为序列特征属性,在进行组合预测时将序列的特征属性和基预测器预测的结果形成元知识,作为元预测器的输入,从而发现并且纠正基预测器的系统偏差。在元预测器中,通过门控网络确定各基预测器的权重,保证了权重的时变性和非负性。预测结果表明,该算法的预测精度较高,具有实际应用价值。
组合预测; 元学习; 门控网络; 最大李雅普诺夫指数; 超短期负荷预测
数学模型是理想的抽象,电力负荷发展的自然规律很难用单一数学模型加以描述。为了提高预测的准确性,减少预测的偏差,预测者往往对同一问题采用多种单一预测方法进行组合,而不只采用一种方法进行预测。组合预测就是综合利用各种预测方法的预测结果,用适当的权系数进行加权平均,组合预测中关键问题是如何筛选模型和求出各种预测模型的权系数。
考虑到不同的预测模型适合具有不同特征属性的负荷序列预测,文献[1]提出了一种基于元学习的时变非线性组合预测算法,该算法将目前已用于分类算法组合的元学习[2,3]思想引入到预测算法的信息融合过程中。在进行组合预测时将负荷序列的特征属性和基预测器预测的结果共同组成元知识,作为元预测器的输入,在元预测器中,使用门控网络确定各基预测器的权重。但该算法中使用的各单一模型是简单的曲线拟合模型,且数量较少,不能满足电力负荷序列的预测要求。本文将该算法进行改进并应用于超短期负荷预测中,结果表明该算法的预测精度高于单一预测算法、目前常用的线性和非线性组合算法和基于元学习的时变非线性组合预测模型。
1 基于元学习的组合预测原理
设f1,f2,…,fn为一组预测算法,共n个;Xp=(xp(1),…,xp(M))是第p个原始输入数据,长度为M。元预测器PM以f1,f2,…,fn在Xp上的预测结果f1(Xp),f2(Xp),…,fn(Xp)和Xp的特征属性ap形成元知识作为输入,输出为组合预测的结果,即
F(Xp)=PM(f1(Xp),f2(Xp),…,
fn(Xp),ap)
(1)
式中,ap={ap(1),ap(2),…,ap(m)},m为特征属性的个数。
当元预测器PM输入不考虑特征属性ap时,采用不同组合预测策略,式(1)退化为各种常用的组合预测方法。
基于元学习的组合预测器结构如图1所示。
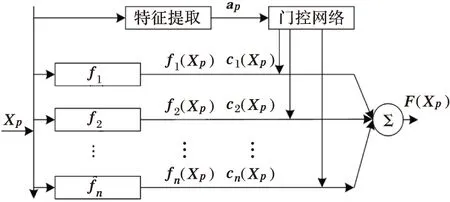
图1 基于元学习的组合预测器结构
它由两部分组成:由各种单一预测算法f1,f2,…,fn组成的基级预测器和以门控网络[4]为核心的元预测器。原始输入数据Xp输入到多个基级预测器,得到基级预测结果f1(Xp),f2(Xp),…,fn(Xp)。将原始输入数据特征向量ap作为门控网络输入,得到各基级预测器的权重c1(Xp)、c2(Xp),…,cn(Xp)。组合预测器最终预测结果为
(2)
门控网络的结构如图2所示。
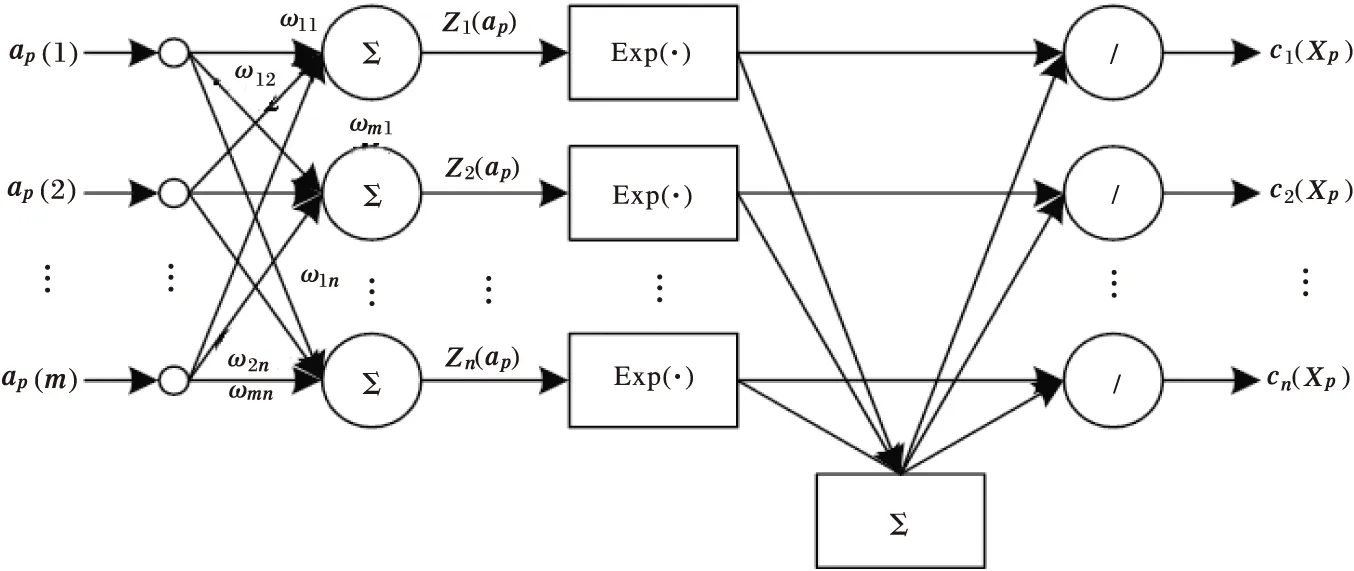
图2 门控网络的结构
在门控网络中使用softmax激活函数,第i个基级预测器的权重ci(Xp)为
(3)
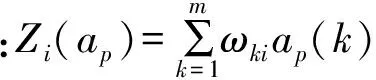
注意到由于Zi(ap)对ap的线性依赖,使得门控网络的输出是ap的一个非线性函数。同时,将softmax激励函数用作门控网络的激活函数能确保满足以下的要求,从而保证了组合预测权值的非负性。
(4)
2 元预测器的学习算法
元预测器的学习目的是确定门控网络的网络参数,使得组合预测结果F(Xp)与相应的期望输出yp两序列拟合最优,可以通过保证训练样本的整体均方误差能量函数EF最小,得到
(5)
式中,P为训练样本的个数。
具体的学习算法可采用常用的各种神经网络学习算法或其改进算法[5]。
3 改进的基于元学习的电力负荷组合预测
本文将文献[1]提出的基于元学习的时变非线性组合预测方法中加入基于最大Lyapunov指数的混沌时间序列预测模型[6,8]并应用于电力负荷超短期预测中。改进后算法增加了基预测器个数,使各单一模型的权重更加优化,提高了模型的自适应性。
3.1 日典型曲线的选取
本文采用变权重灰色关联分析法从历史中选取典型日[9]。具体方法如下。
设x0、xi分别为预测日及历史日各影响因素构成的向量,i=1,2,…,m,则有
x0=[x0(1),x0(2),…,x0(n)]
(6)
xi=[xi(1),xi(2),…,xi(n)]
(7)
称
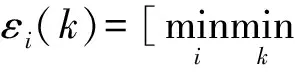
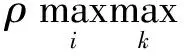
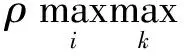
(8)
为x0与xi在第k点的关联系数。其中,Δi(k)=x0(k)-xi(k),ρ分分辨系数,是0到1之间的数,一般取ρ=0.5。
综合各点的关联系数,可得出整个x0与xi的关联度ri为
(9)
由于各气象因素影响负荷的程度不同,采用变权重的灰色关联度方法确定关联度。
(10)
式中,λk为第k个影响因素的权重,体现了不同的影响因素对负荷影响的程度。
当选取了预测日的多条相似日曲线后,选取与预测日关联度最大的历史日为典型日。
3.2 基预测器的选取
考虑到电力负荷序列在局部可以用多项式曲线、指数曲线来近似并且电力负荷时间序列具有混沌特性,本研究选取了一次型多项式曲线、二次型多项式曲线型、三次型多项式曲线型、简单指数曲线模型、基于最大Lyapunov指数的混沌时间序列预测模型作为基预测器。
3.3 特征属性的选取
在元预测器训练阶段,特征属性可直接获得。在预测阶段,由于预测曲线在预测时刻的特征属性和预测日基预测器是未知的,因此分别采用日典型曲线在对应时刻的特征属性和基预测器代替。
由于日典型曲线XS在总体形态上是与预测日曲线Xp相似的,因此可以采用XS的特征属性来近似表征预测日负荷曲线Xp的特征属性。
对于给定的序列XS是否具有混沌时间序列趋势可用序列的Lyapunov指数判断并表征,如混沌时间序列预测模型的最大Lyapunov指数为常数。
因此,选择以下5个特征属性:
(1)预测时刻及其前后共T点的一阶差分均方差ap(1);
(2)预测时刻及其前后共T点的二阶差分均方差ap(2);
(3)预测时刻及其前后共T点的三阶差分均方差ap(3);
(4)预测时刻及其前后共T点的环比系数均方差ap(4);
(5)预测时刻及其前后共T点序列的最大Lyapunov指数ap(5)。
4 结果分析
分别采用一次曲线模型、二次曲线模型、三次曲线模型、简单指数曲线模型、基于Lyapunov指数的混沌时间序列预测模型、简单平均组合预测模型、神经网络组合预测模型、基于元学习的电力负荷组合预测模型和改进的基于元学习的电力负荷组合预测模型对某区域电网2007年3月1日到3月10日,共2 880点的负荷进行预测。神经网络组合预测模型和本文基于元学习的电力负荷组合预测模型训练过程中采用的训练样本是2007年7月1日到7月31日的8 928个训练样本。
元预测器的学习算法过程具体如下。
步骤1网络参数的初始化:将ωki赋以随机的初始值。其中:k=1,…,m;m为特征属性的个数;i=1,…,n;n为基级预测器个数。
步骤2输入学习样本Xp=(xp(1),…,xp(M))及相应的期望输出g(Xp)。其中:p=1,…,P;P为训练样本数
步骤3网络的自学习:利用当前网络参数计算出网络的输出
(11)
步骤4计算瞬时梯度向量

[fi(Xp)-F(Xp)]·ap(k)}
(12)
步骤5修改网络参数
(13)
神经网络组合预测模型中通过比较,采用了函数逼近能力较好的RBF网络作为组合器。预测结果如表1所示。
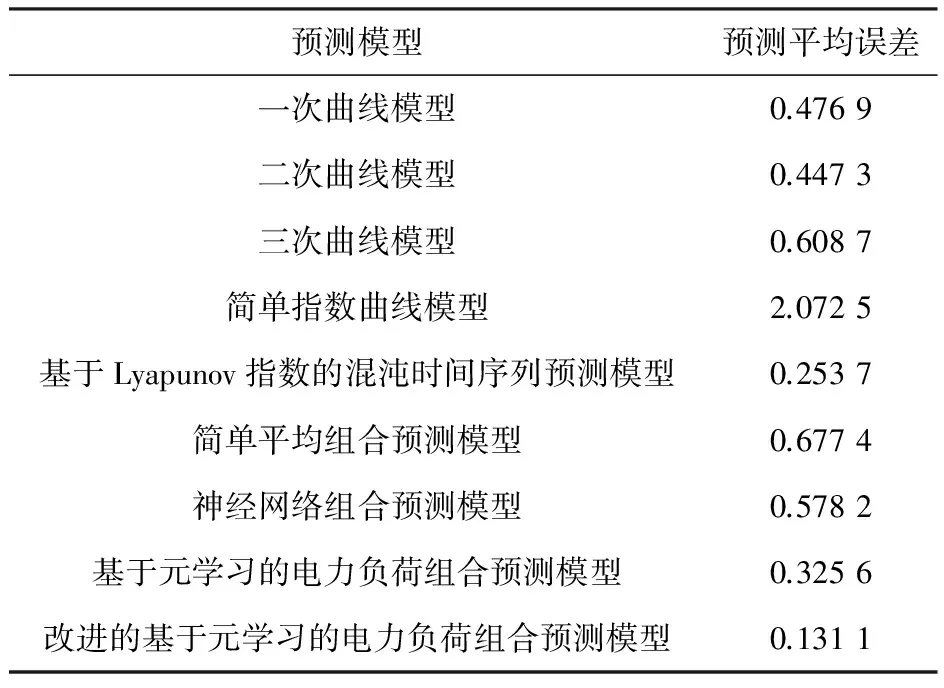
表1 预测结果比较
由表中结果可见,改进的基于元学习的电力负荷组合预测模型的预测结果优于各种单一预测模型的预测结果、目前常用的线性和非线性组合算法和基于元学习的电力负荷组合预测模型。
取2007年3月8日的预测结果,如图3所示。由图3可知,改进的基于元学习的电力负荷组合预测模型的预测结果优于神经网络组合预测模型的预测结果,这主要是因为该模型在进行组合预测时将负荷序列的特征属性和基预测器预测的结果形成元知识,可在一定程度上减少系统偏差,提高组合预测精度。同样也优于基于元学习的电力负荷组合预测模型。这主要是因为在原有方法上的基预测器中增加了基于Lyapunov指数的混沌时间序列预测方法,有利于各单一模型权重优化,提高了预测模型的自适应性。
表2为图3中三个预测时刻,采用改进的基于元学习的电力负荷组合预测模型进行预测时,不同基预测模型的权重。从表2中可知,基于Lyapunov指数的混沌时间序列预测模型在该三个时刻的权重均高于其他模型,这说明电力负荷时间序列具有混沌特性,将该模型作为基预测器在元预测器中使权重更加优化,有利于提高电力负荷预测精度。
由表中可见,对09:00时刻负荷进行预测时,相比于基于Lyapunov指数的混沌时间序列预测模型,二次曲线模型权重较高,是因为在该时刻为拐点,且局部变化比较快,所以用二次曲线模型进行预测效果要好;对12:30时刻和23:15时刻负荷进行预测时,相比于基于Lyapunov指数的混沌时间序列预测模型,一次曲线模型权重较高,是因为在该时刻为拐点,且局部变化比较缓慢,所以用一次曲线模型进行预测效果要好。因此,改进的基于元学习的组合预测模型保证了组合预测的时变性。
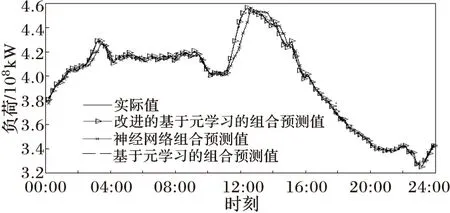
图3 改进的基于元学习的组合预测模型与神经网络组合预测模型和基于元学习的组合预测模型预测结果比较
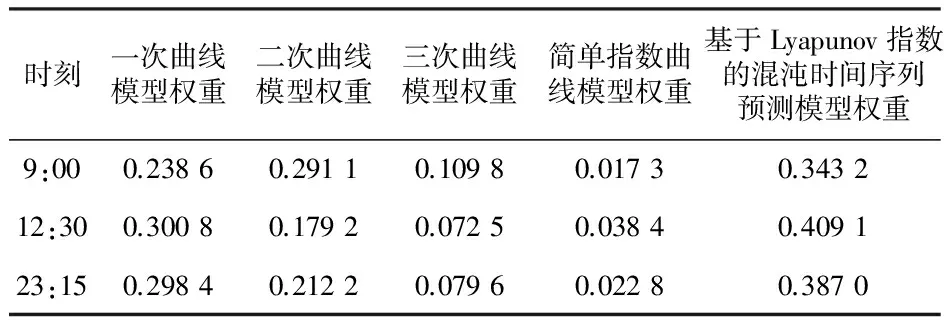
表2 不同时刻基预测器的权重
从表中可知,各权重都为非负数,因此基于元学习的电力负荷组合预测模型保证了组合预测的非负性。同时,从该表还可以看出简单指数曲线模型预测结果不良,因此在各时刻预测时所占的权重都不大。由此可见采用本文预测模型可有效剔除不良模型,实现模型的合理选择。
5 结论
改进的时变非线性负荷预测组合算法的预测精度高于单一预测算法、常用的线性和非线性组合预测算法和基于元学习的时变非线性负荷预测组合模型。由于电力负荷时间序列具有混沌特性(结果分析中已经证明),将基于Lyapunov指数的混沌时间序列预测模型作为基预测器,在元预测器中使权重更加优化,比原有的基于元学习的时变非线性负荷预测组合算法的预测准确率更高。同时根据各模型的权重,可以剔除权重较小模型,实现模型合理选择。所以该方法对于电力负荷预测人员进行准确的电力超短期负荷预测有实际的指导意义。
[1] 罗滇生,肖伟,何洪英(Luo Diansheng, Xiao Wei,He Hongying). 基于元学习的时变非线性负荷预测组合算法(Time-varying nonlinear power load combined forecasting algorithm based on meta-learning)[J].继电器(Relay),2007,35(17):12-16,21.
[2] Wang Xiaozhe, Smith-Miles K, Hyndman R. Rule induction for forecasting method selection: Meta-learning the characteristics of univariate time series [J]. Neurocomputing,2009,72 (10/11/12):2581-2594.
[3] Alexandros K, Melanie H. Model selection via meta-learning: a comparative study[J]. International Journal on Artificial Intelligence Tools, 2001,10(4): 406-413.
[4] Moerland P. Mixtures of experts estimate a posteriori probabilities [J]. Lecture Notes in Computer Science,1997,(1327): 499-504.
[5] 丁军威,孙雅明(Ding Junwei, Sun Yaming).基于混沌学习算法的神经网络短期负荷预测(Short-term load forecasting using chaotic learning algorithm for neural network)[J].电力系统自动化(Automation of Electric Power Systems),2000,24(2): 32-35.
[6] 郑永康,陈维荣,蒋刚,等(Zheng Yongkang, Chen Weirong, Jiang Gang,etal).基于混沌理论的短期负荷局域多步预测法(Local-region multi-steps load forecasting model based on chaotic theory)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(4): 76-79.
[7] 张智晟,马龙,孙雅明(Zhang Zhisheng,Ma Long, Sun Yaming).混沌理论和支持向量机结合的负荷预测模型(Load forecasting model using chaos theory and support vector machine)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(6): 31-35.
[8] Eckmann J P, Oliffson K S. Lyapunov exponents from time series [J].Physical Review A,1986,34(6):4971-4979.
[9] 李如琦,徐姣,魏立(Li Ruqi,Xu Jiao,Wei Li). 基于相似日和分时段分形插值的短期电力负荷预测(Short-term electric power load forecasting based on similar days and time-segment fractal interpolation)[J].现代电力(Modern Electric Power),2009,26(2): 37-41.
[10]康重庆, 夏清,刘梅. 电力系统负荷预测[M].北京:中国电力出版社,2007.
陈锦攀(1985-),男,硕士研究生,研究方向为负荷预测、电网规划、电力市场及其技术支持系统。Email:xu_19pan@163.com
罗滇生(1971-),男,博士,教授,研究方向为电力市场理论研究及应用、电力系统在线监测。Email:hhylds@sohu.com
周 勇(1971-),男,高级工程师,主要从事调度管理工作。Email:hncszy2345@sina.com
AnImprovedTime-varyingNonlinearPowerLoadCombinedForecastingAlgorithm
CHEN Jin-pan1, LUO Dian-sheng1, ZHOU Yong2, HE Hui2, XIAO Shi-yong3
(1.College of Electrical and Information Engineering, Hunan University,Changsha 410082, China;2.Electric Power Dispatching and Communication Bureau of Hunan Electric Power Corporation, Changsha 410007,China;3.Loudi Electric Power Bureau of Hunan Electric Power Corporation,Loudi 417000, China)
An improved combined algorithm of time-varying nonlinear forecasting is presented in order to improve the accuracy of ultra short-term power load forecasting. The algorithm increases chaotic time series prediction model based on the largest Lyapunov exponent in base predictors. The largest Lyapunov exponent is a kind of feature attributes of series. Meta knowledge formed by the results of base predictors and feature attributes of series is used as inputs of meta predictor when combined forecasting is applied. System bias can be founded and rectified. The weights of base predictors are calculated using gating network in metal predictor. Weights of base predictors are time-varying and non negative. The new algorithm is applied in ultra short-term load forecasting. Results show that forecasting precision of the proposed method is higher and it has practical application value.
combined forecasting; meta learning; gating network; the largest Lyapunov exponent; ultra short-term load forecasting
TM715
A
1003-8930(2012)01-0115-05
2010-06-29;
2010-07-14
