电流突变抑制与智能化谐波检测系统

马立新， 林家隽， 肖 川， 鲁 奕

(上海理工大学电气工程系， 上海 200093)

电流突变抑制与智能化谐波检测系统

马立新， 林家隽， 肖 川， 鲁 奕

(上海理工大学电气工程系， 上海 200093)

针对网侧电流的电能质量问题，设计了一个并联型有源电力滤波器系统。该系统采用神经网络谐波检测方法，提高了检测的实时性和精度；补偿装置采用周期采样控制方法，便于实际应用；负载端加入隔离变压器，获得了更好的补偿效果。该方法具有精度高、延迟小、补偿效果好的优点，使得该有源电力滤波器系统更适合工程中的应用。MATLAB仿真结果验证了该系统的有效性和可行性。

谐波； 有源电力滤波器； 神经网络； 补偿； 总谐波畸变

有源电力滤波器是一种动态抑制谐波的电力电子装置，能对变化的谐波进行实时检测及补偿，从而抑制电网中谐波，使电能质量达到国家标准。在文献[1]基础上，加入补偿装置和隔离变压器，通过MATLAB仿真验证了神经网络谐波检测方法应用在有源电力滤波器系统中的有效性与可行性，与采用ip-iq谐波检测方法的有源电力滤波器补偿结果比较，该系统具有更好的补偿效果。

1 并联型有源电力滤波器的工作原理

并联型有源电力滤波器的工作原理如图1所示，有源电力滤波器通过采样获得电流信号，经过谐波检测环节计算出谐波电流，再通过补偿装置产生与谐波电流反相的电流ic注入电网，从而达到抑制谐波的目的[3]。

图1 APF原理

2 谐波检测方法

该方法是将信号用FFT分解，即得到各次谐波的幅值和相位。缺点是具有较大的延时[2]。另一种方法是ip-iq谐波检测方法，其原理如图2所示。

图2 ip-iq谐波检测方法的原理

3 控制方法

一般有两种控制方法，其一是滞环控制法，滞环控制法根据给定补偿信号与实际补偿信号的误差来控制逆变器的开关动作[2]。第二种方法是三角波比较法，如图3所示，此方法输出控制信号的频率等于三角载波的频率，可提高功率器件的使用寿命[3]。

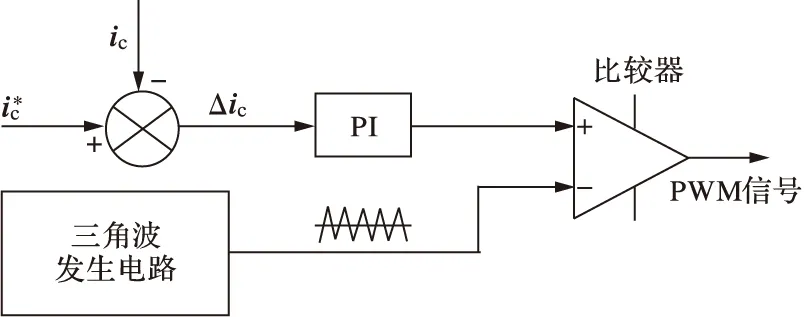
图3 三角波比较法原理

4 APF系统设计

4.1 基于BP神经网络的谐波检测方法

基于BP神经网络与锁相环相结合的谐波检测原理如图3所示，当电网侧三相电流经过锁相环时可得与各相基波电流同相位的单位基波信号iaf1(t)、ibf1(t)、icf1(t)，再将其乘以由神经网络输出的三相电流基波幅值Ia(t)、Ib(t)、Ic(t)便可得到当前时刻每一相电流的基波分量iaf(t)、ibf(t)、icf(t)，再利用各相电流采样值ia(t)、ib(t)、ic(t)减去各自的基波分量iaf(t)、ibf(t)、icf(t)可得三相电流的谐波量iah(t)、ibh(t)、ich(t)。该方法去掉了延时较高的低通滤波环节，提高了谐波检测的速度和精度[2]。

图4 BP神经网络与锁相环相结合的检测原理

本文定义一个三层的BP神经网络，输入层为6个神经元，隐层为41个神经元，输出层为3个神经元，取三相电流的采样值和一个周期内三相电流的最大值作为BP神经网络的输入，将FFT理论计算出的三相基波电流的幅值作为网络期望，采用BFGS拟牛顿算法对网络进行离线训练，并将训练后神经网络生成simulink模块[1]。

4.2 周期采样控制方法

图5为周期采样控制方法的原理。周期采样控制方法主要是根据有源电力滤波器输出电流与参考电流的比较结果在采样脉冲的上升沿改变PWM脉冲的状态。如果在采样脉冲的上升沿补偿电流icgt;iret，则PWM脉冲为正，控制有源电力滤波器的逆变器开关使补偿电流减小；如果在采样脉冲的上升沿补偿电流iclt;iret，则PWM脉冲为0，控制有源电力滤波器的逆变器开关使补偿电流增加。周期采样控制方法的优点是控制非常简单，工程应用中实现起来极为简单，器件的开关频率被限制在采样时钟脉冲的频率以内[2]。

图5 周期采样控制

4.3 隔离变压器

隔离变压器指1∶1的变压器，其原理如图6所示，当一次侧绕组上加上电压U1时，流过电流I1，在铁芯中就产生交变磁通Φ1，在它作用下，两侧绕组分别感应电势E1、E2，感应电势公式为

E=4.44fNΦm

(3)

式中：E为感应电势有效值；f为频率；N为匝数；Φm为主磁通最大值。

本文所设计的系统中，在负载与电网之间增加隔离变压器，对谐波电流起到了一定的缓冲作用，获得了更好的补偿效果。

图6 隔离变压器的原理

5 仿真结果及总结

为了验证所述方法的有效性，本文建立了MATLAB仿真模型(见图7和图8)。

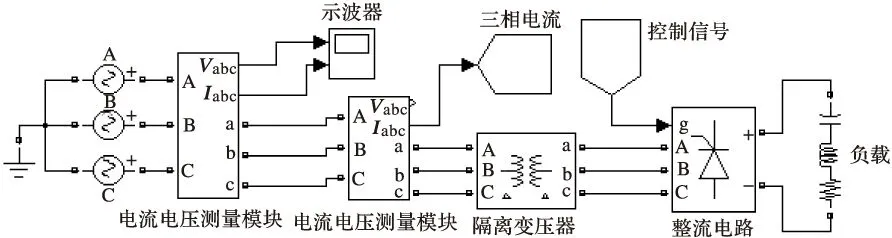
图7 谐波源的MATLAB模型

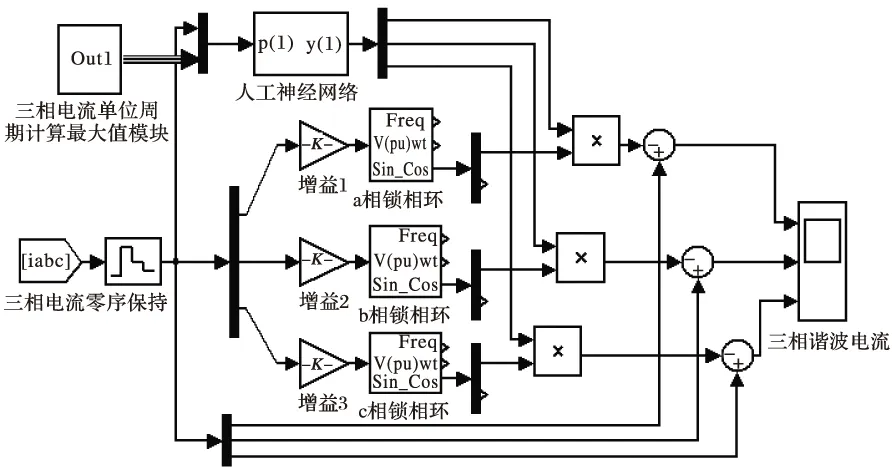
图8 文中谐波检测方法的MATLAB模型

仿真实验条件：三相电源带整流负载，其中，负载参数为R=100 Ω，L=1.8 H，C=0.6 F，在0.5 s时触发角由0°变为30°。

网侧电流波形如图9所示，0.5 s时，触发角由0变为30°，电流波形发生明显变化。0.2～0.3 s电流的THD如图10所示(为16.42%)，0.8～0.9 s电流的THD如图11所示(为24.41%)，大大超过了规定的标准。

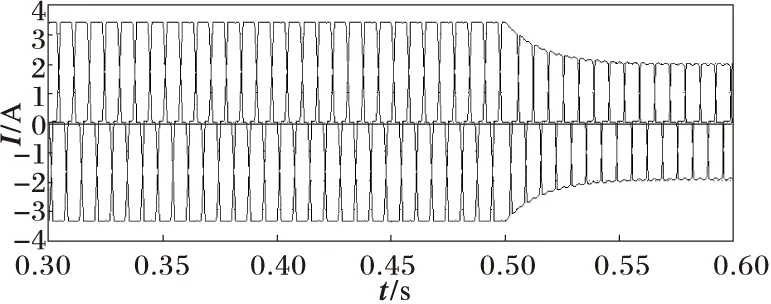
图9 A相负载电流波形

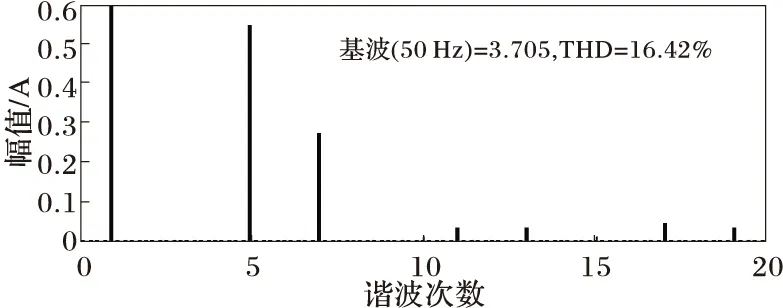
图10 0.2～0.3 s网侧电流总畸变率

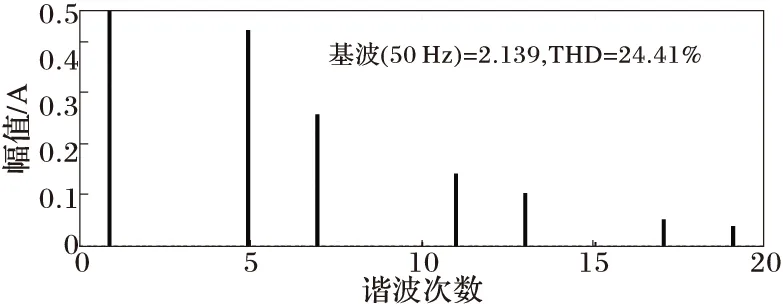
图11 0.8～0.9 s网侧电流总畸变率

基于BP神经网络的谐波检测方法与ip-iq算法检测的基波电流如图12所示，其中，ip-iq谐波检测方法检测出的基波延迟大，且输出波形的幅值也不稳定，影响了谐波实时检测的速度和精度，以及对后面谐波的补偿；相比之下，基于BP神经网络的检测方法检测的基波延迟小，幅值稳定，具有良好的自适应能力。

(a) 神经网络法

(b) 瞬时无功法

两种方法检测出的谐波如图13所示，可见所构建的神经元网络检测基波的速度和精度都大大优于ip-iq检测方法。它们所检测出来的谐波电流，ip-iq检测方法要在0.2 s之后才能检测出谐波分量，而本文所采用的方法在0.1 s之前就检测出了谐波分量；由于BP神经网络检测方法的基波检测精度高，所以在谐波检测精度上较ip-iq检测方法也有一定的提高。

经过补偿装置补偿后，网侧电流波形如图14和图15所示，可以看出电流波形中存在“尖峰”。电流的THD如图16和图17所示，经过补偿后的波形还未达到允许的5%以内[6]。

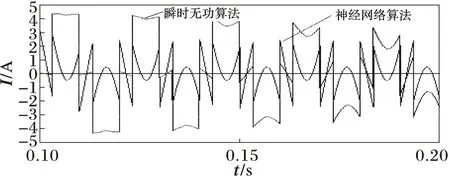
图13 0.1～0.2 s内两种方法检测的谐波电流

图14 不加隔离变压器补偿后0.20～0.24 s电网侧电流波形

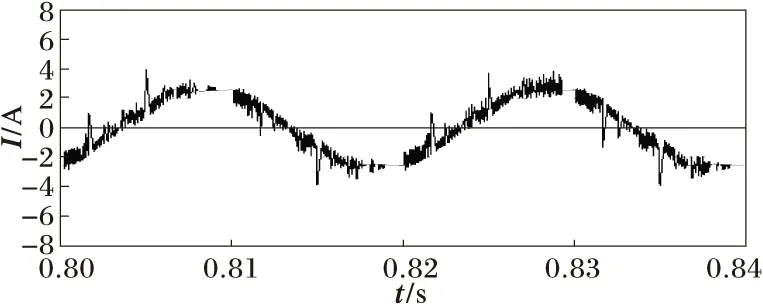
图15 不加隔离变压器补偿后0.80～0.84 s电网侧电流波形

经过对波形的比较分析可知，“尖峰”产生的原因在于跟踪器未能很好跟踪到电流波形的跳变，故而产生“尖峰”，影响了电能质量。本文提出了一种解决办法，即在负载端加入隔离变压器。如图18所示，加入隔离变压器后，电流波形的跳变有了明显改善，因为根据楞次定律，电感对电流的变化有一定的阻碍作用，使电流的变化率降低了，这样有利于跟踪器更好地跟踪电流的变化，提高了补偿的效果。加入隔离变压后，0.38～0.41 s内，经APF补偿后的电网侧电流波形如图19所示，跟踪器能很好地跟踪谐波电流，消除了“尖峰”，提高电能质量；从0.38 s起，取5个周期的波形进行FFT分析，如图20所示，电网侧电流的THD值为1.88%，达到允许范围内；0.68～0.75 s电网侧电流波形如图21所示，对该波形进行FFT分析，结果如图22所示，THD值为3.32%，均在GB/T 14549-93标准范围内。仿真结果如表1所示。

图16 补偿后0.2～0.3 s网侧电流总畸变率

图17 0.80～0.9 s网侧电流总畸变率

图18 有、无隔离变压器负载端电流对比(A相)

图19 加入隔离变压器后，0.38～0.41 s补偿后电网侧电流波形

图20 加入隔离变压器后，0.25～0.35 s内电网侧电流总畸变率

图21 加入隔离变压器后，0.68～0.76 s补偿后电网侧电流波形

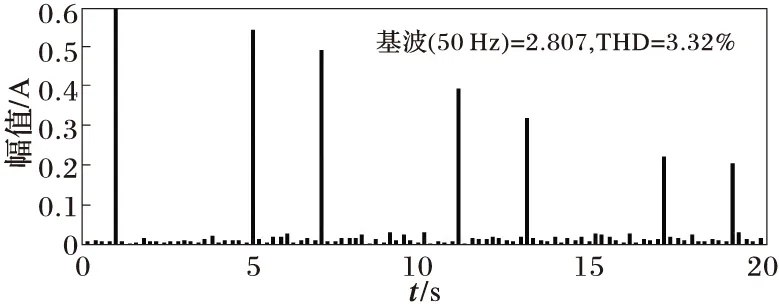
图22 加入隔离变压器后，0.68～0.75 s内电网侧电流总畸变率

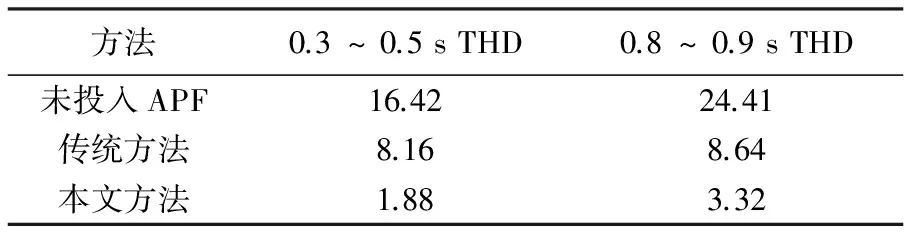
表1 网侧电流总畸变率

6 结语

本文在论文BP神经网络和锁相环相结合的谐波检测方法[1]的基础上，根据所提出的新方案，搭建了谐波补偿装置，进一步完善整个有源电力滤波器系统，经过MATLAB建模和仿真验证了其可行性和正确性。通过与传统ip-iq谐波检测方法的比较，可以看出本论文中的系统具有良好的实时性和精确性以及自适应能力，满足APF的谐波检测要求；通过有无隔离变压器的仿真结果对比，可以看出本文提出的在负载端加入隔离变压器的方法可以大大改善补偿后电流的波形，使电流的总畸变率在允许的范围之内。本文提出的有源电力滤波器系统具有简单易实现，检测精度高、实时性好、自适应性强的特点，良好的补偿效果适合工程应用。

[1] 马立新，肖川，林家隽，等(Ma Lixin, Xiao Chuan, Lin Jiajun，etal).神经网络和锁相环相结合的谐波检测方法(Method of harmonic detection based on neural network combined with phase-locked loop)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2011，23(3): 24-29.

[2] 姜齐荣.有源电力滤波器-结构·原理·控制[M]. 北京：科学出版社，2005.

[3] 张林利，王广柱(Zhang Linli, Wang Guangzhu).一种基于人工神经网络的谐波测量新方法(New artificial neural network approach for measuring harmonics)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2004，16(2)：40-43.

[4] 王兆安，杨军，刘进军．谐波抑制和无功功率补偿[M]. 北京：机械工业出版社，1998.

[5] 葛哲学,孙之强. 神经网络理论与MATLABR2007实现[M]. 北京：电子工业出版社,2007.

[6] GB/T 14549-93,电能质量 公用电网谐波[S].

[7] 王群，吴宁，王兆安(Wang Qun, Wu Ning, Wang Zhao'an). 一种基于人工神经网络的电力谐波测量方法(A measuring approach of power harmonics based on artificial neural network)[J]. 电力系统自动化(Automation of Electric Power Systems)，1998，22(11)：35-39.

[8] Ma L, Oda M, Miyajima H. A consideration on the ability of multilayer higher order neural networks [J]. Trans of the IEEE of Japan, 1999, 119-C(3): 421-422.

马立新(1960-)，男，博士，教授，研究方向为电力系统稳定性与优化运行，电气系统故障诊断与模式识别，电力能效测评，群体智能与智能电网。Email:malx_aii@sina.com

林家隽(1987-)，男，硕士研究生，研究方向为电能质量控制。Email:linjiajun1987@gmail.com

肖 川(1983-)，男，硕士研究生，研究方向为电能质量控制。Email:xiaoch1222@163.com

CurrentMutationSuppressionandIntelligentHarmonicDetectionSystem

MA Li-xin， LIN Jia-jun， XIAO Chuan， LU Yi

(Department of Electrical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

For the power quality problem, a design of shunt active power filter system was proposed in the paper. The system uses neural network harmonic detection method to improve the real-time and accuracy of detection; its compensation device uses periodic sampling control, and ease to be applicated; load by adding isolation transformers, to obtain better compensation effect. The proposed method has high precision, low delay, and the benefits of a good compensation effect of active power filter system is more suitable for engineering applications. MATLAB simulation results validate the effectiveness and feasibility of the system.

harmonic； active power filter (APF)； neural network； compensation； total harmonic distortion (THD)

TP273.22

A

1003-8930(2012)01-0049-05

2011-07-26；

2011-09-19

国家科技部政府间科技合作项目(2009014)；上海市高等学校高地建设项目