快速计算浓缩立方体的方法

涂建新，游进国

(昆明理工大学信息工程与自动化学院，云南昆明 650500)

快速计算浓缩立方体的方法

涂建新，游进国

(昆明理工大学信息工程与自动化学院，云南昆明 650500)

为了能够更快地生成浓缩立方体，提出了一种新的通过各个值的频率对格子的空间进行分解的MM－Cubing算法:用一种计数、排序算法和相关的数据结构来计算每一个值出现的频率，同时提供一种数据结构来方便主要值的选取和计算其子空间;选取主要值，聚会稠密的子空间，递归调用稀疏子空间.实验结果表明:MM－Cubing算法优于MinCube算法和SQCube算法.

浓缩立方体;格子;空间;算法

0 引言

自从数据仓库中联机分析处理(On－Line Analysis Processing，以下简称:OLAP)和数据立方体的提出，有效计算数据立方体成为一个热门话题，数据立方体的计算方法有:用简单或者复杂的值计算完全和冰上立方体［1－2］;对压缩的数据立方体进行近似计算，如准立方体［3］;用索引进行封闭立方体计算，如浓缩立方体、侏儒立方体和商立方体［4－5］;选择物化视图［6］.

语义OLAP的思想被许多学者提出，即对整个数据立方体的数据用一种特殊的压缩存储结构存储，这种结构不但能对所有立方体的元组进行表示和生成，而且对整个数据立方的操作性能(如查询、维护等方面)有极大的改善，比如浓缩立方体、商立方体树等.浓缩数据立方体产生的单一元组分区通过使用聚合计算，该元组将该分区对应的属性及其超集对应的元组都包含在其中，从而降低数据立方体的大小.商立方体树［7］使用的是等价类，它把具有相同聚合值的元组放在一起，同时将每一个等价类的在语义上对应的上界计算出来，进而降低了数据立方体对存储空间的需求.

Wang Wei等人［8］于2002年基于基本单一元组，介绍了浓缩数据立方体应该满足的性质，并展示了一种生成最小浓缩数据立方的MinCube算法.因为MinCube算法生成最小浓缩数据立方体有一定困难，所以作者决定用压缩率的降低来换取体积的减少，提出了并不保证生成最小浓缩立方体的启发式算法 ButtomUpBST以及其优化算法ReorderButtomUpBST，这两个算法虽然速度很快，但压缩率明显低于最小浓缩数据立方体的压缩率.

王琢等人于2005年在ButtomUpBST算法的基础上，提出一个可以比较快速生成最小浓缩数据立方的SQCube算法［9］，但是该算法需要进一步的优化.

本文根据在一个维度中每一个值出现的频率不同，从而对格子空间进行分解，提出一种用MM－Cubing计算浓缩立方体的方法，实验结果表明该方法比Mincube、ButtomUpBST和SQCube算法能更好生成浓缩立方体.

1 分解格子空间

在数学上，每一个单元可以用(a，b，c，d，…)来表示:a、b、c和d是一个与其维度相对应的值，或者用*来表示所有值.这些单元形成格子空间，每一个格子空间的基数等于1加上输入元组相对应的每一个维度上的基数.

MinCube、ButtomUpBST和SQCube算法是自上而下、自底向上或者同时使用，而忽略了数据的值密度.在一个维度中，对于所有的非*值，有些值出现的频率比较高，而有些值出现的频率很低，为了使执行效率更高和有很好的可扩展性，计算浓缩立方体，有必要对于不同频率的值进行不同的处理.频率值的大小反映了单元的频率，将频率高的值作为主要值(major value)，频率低的值作为次要值(minor value).用D表示输入元组的维度数量，在主要值与次要值之间对格子空间进行分解，它们的值用分开点来表示，新的网格结构有3D个节点.用M表示主要值，I表示次要值，*表示所有值.一个3-D格子可以表示为({M，I，*}，{M，I，*}，{M，I，*})，一个次要值也应该至少出现1次，一个小于1的值不会出现在浓缩立方体中.

由于一个主要值出现的频率很高，所以与*共享计算是比较好的;而对于一个次要值，需要进一步的计算.因此，将格子空间分为以下4个子空间:({M，*}，{M，*}，{M，*})，(I，{M，I，*}，{M，I，*})，({M，*}，I，{M，I，*})，({M，*}，{M，*}，I).这些子空间没有交集，所有的子空间之和刚好是原始格子空间，如图1所示.

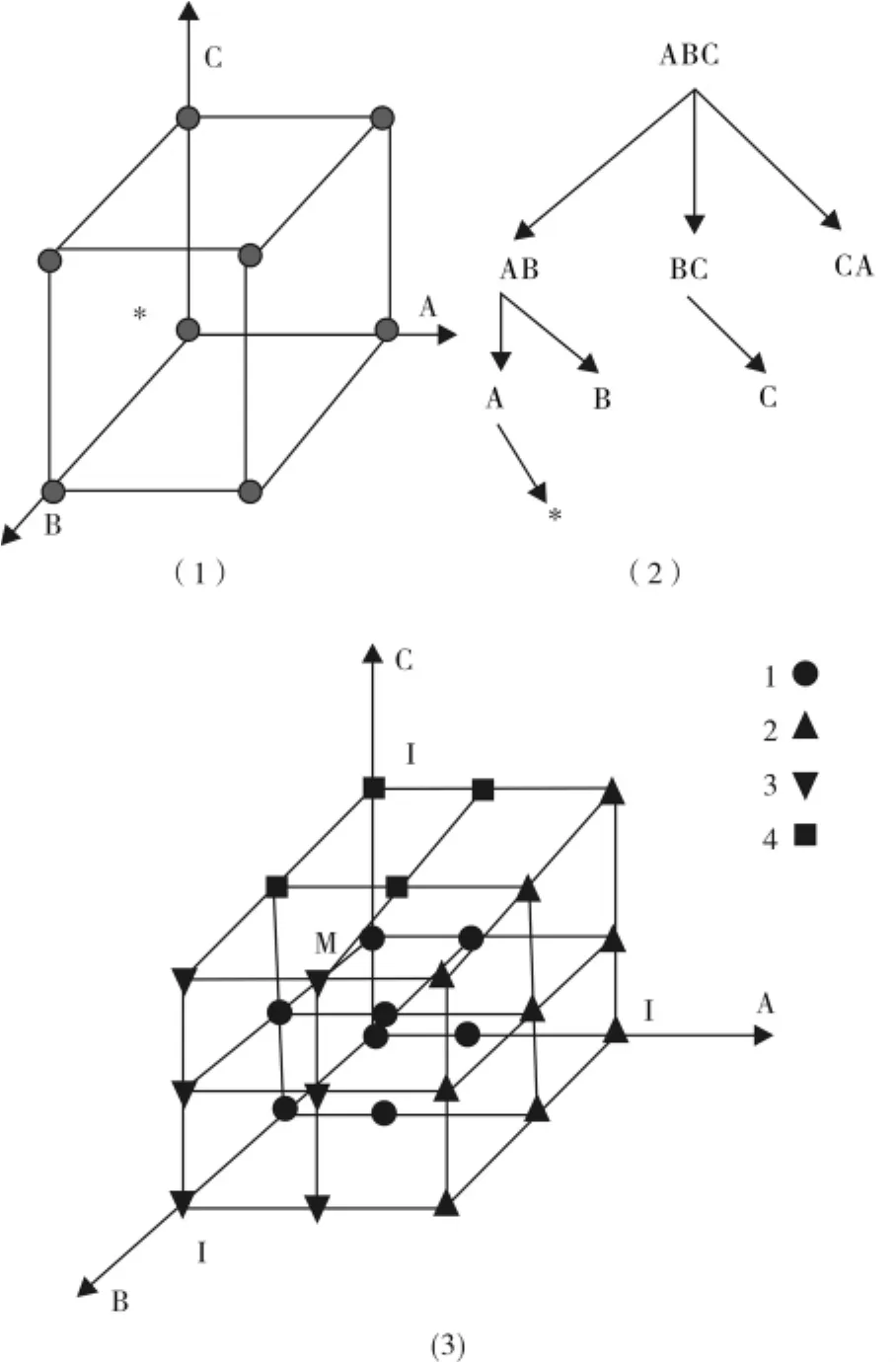
图1 (1)传统格子空间(2)传统格子树(3)分解新的格子空间Fig.1 (1)Traditional lattice space(2)Traditional lattice tree(3)Factorization of the new lattice space

在第一个子空间({M，*}，{M，*}，{M，*})中，每一个维度的值是一个主要值或者是*，在这个子空间中的数据出现的频率可能会很高，子空间相对密集，为密集子空间.

在第二个子空间(I，{M，I，*}，{M，I，*})中，所有的值在第一个维中是次要值，数据出现的频率不会很高，由于次要值的值不是很大.

第三个子空间({M，*}，I，{M，I，*})类似于第二个子空间，数据出现的频率不会很大，但是有一点不同，在第一个维度中其值只能是主要值和*.

第四个子空间({M，*}，{M，*}，I)除了有两个维度的值必须是主要值和*外，类似于第三个子空间.

第一个子空间为密集子空间，其余三个子空间为稀疏子空间，在稀疏子空间中可以通过递归调用探测其他的密集子空间.

格子空间的分解方法并不是唯一的，也可以将格子空间分解为以下5个子空间:

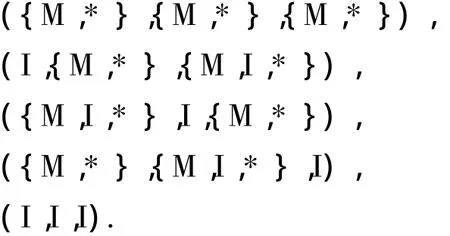
2 MM-Cubing算法

MM－Cubing算法:首先按照图1中(3)的方法分解格子空间，然后计算聚合密集子空间和递归调用稀疏子空间.

在分解格子空间之前，首先应该计算在每一个维度中值出现的频率，然后按照从大到小进行排序，最后确定哪个值是主要值或次要值.

MM－Cubing计算浓缩立方体算法输入的是一个关系表R，输出的是浓缩立方体.

2.1 计数和排序

选择一种数据结构来计算每一个值的频率，从而选择主要值并计算子空间.

假设有表1所示的输入数据，则输出结果如表2所示.

表1 输入数据Table 1 Data of input

表2 输出结果Table 2 Result of output

数据结构的选择对于性能提升有很大的影响，因此使用桶排序算法同时使用两个数组(一个大小为一个维度基准的大小和另一个的大小为输入元组链表的大小)进行计算，输出的数据结构是数组的结构和元组ID的数组，称之为共享数组，如图2所示.

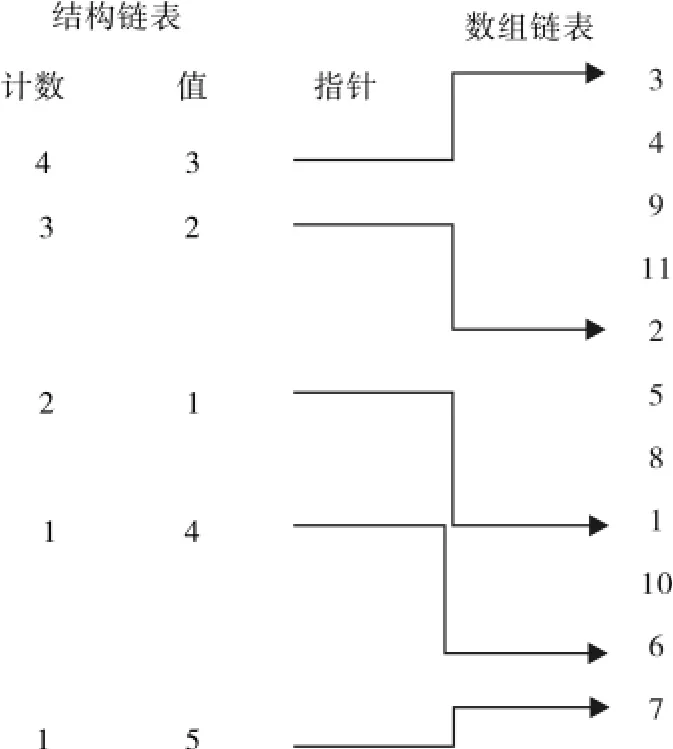
图2 共享数组结构Fig.2 Shared array structure

2.2 选择主要值

主要值赋值应该保证运行时间最小.然而这个算法是递归的，很难估计递归调用的时间，由于这依赖于在子空间中主要值的赋值，因此给出一个主要值选择的规则——在一个维度中的所有主要值应该大于在相同维度中的次要值，这就是通过频率来对值进行排序的原因.

运用一个启发式的方法来选择主要值:定义一个量度，work_done完成工作作为总量，完成工作通过聚合

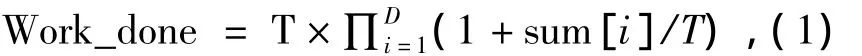
式(1)中:T为元组的数量，sum［i］为在维度i中主要值的元组个数，D为维度的数量.

聚合表的大小可以计算为∏i(1+MC［i］)，其中MC［i］为在第i个维度中主要值的数量.

希望主要值是最大值而聚合表的大小不会超过一个常量的大小，定义的完成工作来自于这样一个算法:用一个哈希表来存储所有的聚合单元，这个哈希表的键值是聚合单元自己，值是这个单元的出现频率.这个方法需要T×2D个步骤完成.尽量将work_done放在密集的子空间中，由于使用的是同时聚合，因而当数据密集的时候效果很好.

使用一个贪心方法来对主要值进行选择.首先，所有的非*值是次要值，反复从每一个维度中频率较大的值中选择来作为最有可能的次要值，让其作为一个主要值直到到达刚开始时定义表的大小.

在每一个维度中出现频率最高的值，定义一个权值，用工作增长的比例除以空间增长比例进行计算求得.这个权值最高的值很有可能作为一个主要值.由于使用的是一个共享数组结构，很容易找到每一个维度的最高频率值，如果有多个的，选择最先出现的那个作为主要值.

2.3 对密集空间进行同时聚合

所有的聚合值放在一个大小为维度D的数组A［b1］［b2］…［bi］(i=1，2，3，…，D)中，bi的范围从0到MC［i］之间，子空间0对应一个*值.同时聚合分为两个步骤:寻找每一个元组的基本单元，进行聚合操作.每一个元组有一个相对应的基本单元，很难知道哪个基本单元与一个元组相对应，虽然在主要值－编号表中没有值，但是我们可以计算所有元组的基本单元，在共享数组的帮助下更加有效，我们用一个数组B［元组］［维度］来存储相对应的子空间.仅仅需要遍历一次共享数组就可得到子空间数组，进而知道每一个元组相对应的基本单元.

这个问题的关键是如何处理不是主要值的值，如果对一个不是主要值的值赋给它一个新的主要值编号，这个聚合表的大小将会是2D，即使没有主要值，这使得当维度大于30的时候，使用MM－Cubing是不可能的，然而，如果让非主要值与*共享空间，主存空间将会大大节省，这个方法需要一个与A大小相同的辅助数组C，在数组C中，所有的元组都有相对应的基本单元，在数组C中子空间0表示所有的非主要值，而在A中表示为*值，所以有

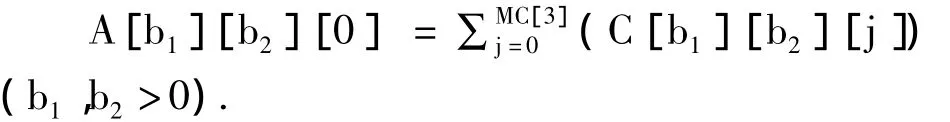
为了节省内存，最好使用一个数组为A和C，通过合理安排聚合的顺序，为了效率，最好将A转换为一个D维数组来实现，因为每一个元组将会只用到一个子空间，数组B也是一个D维的，反过来也节省了许多的内存.

2.4 对稀疏子空间进行递归调用

对稀疏子空间(I，{M，I，*}，{M，I，*})通过递归调用进行计算，可以得到:

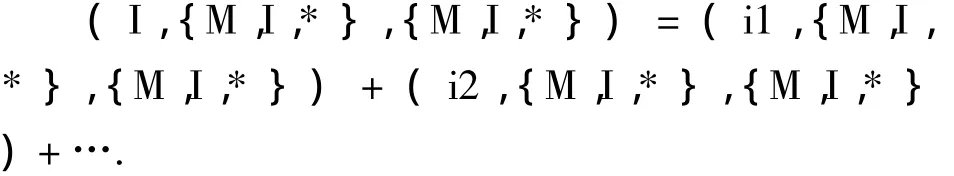
为了使每一个子空间的右边相等，在第一个维度中是一个值，可以通过第一个维度的值分割所有的元组，对于第一个维度中的最小值运用递归调用MM－Cubing算法.

在计数和排序步骤，已经得到在一个指定维中所有元组的相同值.仅仅需要传递一个元组的编号，而不是元组本身，对于递归调用，在这种方式下，可以节省内存和提升程序执行速度.所有子空间的计算与第一个基本相同，但是有一点不同，例如，对于子空间({M，*}，I，{M，I，*})，在第一个维度中的主要值是主要值或者是*，由于(I，I，{M，I，*})在第一个子空间已经计算了，解决这个问题的方法是将第一个维度中的次要值设置成一个特殊的非聚合值，然后计算这个子空间，这个次要值重新存储，通过共享数组结构可以很方便的进行设置和恢复操作从非聚合值中.

3 试验结果及分析

测试环境:CPU为Intel Core 2.27GHz，512MB内存;使用的是C++语言;基本关系和所有输出的浓缩数据立方存储在 SQL Server2008数据库中.当维度和每一个维度的基数一定的时候，分别用MinCube、ButtomUpBST、SQCube和MM-Cubing算法对天气数据集进行计算.各种算法生成浓缩立方体速度如图3所示，D(dimension)表示维数，C(cordandial)表示基数.

从图3可以看出MM－Cubing算法生成浓缩数据立方体的速度是最快的.因为MM－Cubing将格子空间分解为一个密集的子空间，没有进行递归调用，所以 MM－Cubing算法能够达到很高的速度.

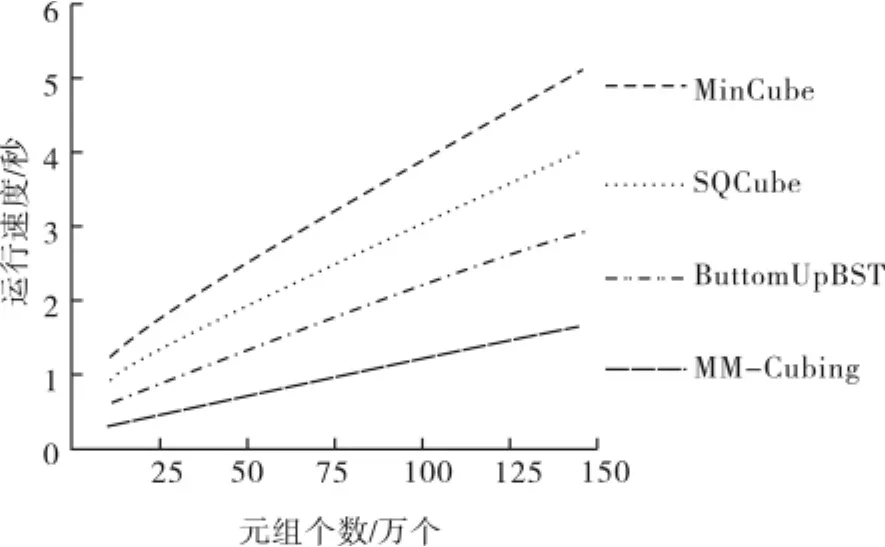
图3 维数为8，基数为100时，各种算法生成浓缩立方体速度的比较Fig.3 D=8 C=100 all kind of algorithms generate condensed cubes speed

4 结语

与传统基于格子的算法不一样，MM－Cubing算法通过分解格子空间，维度的重新排序会加快计算，通过生成子空间用很小的维度，不同的主要值选择会影响效率，贪心策略执行得很好，但是可以通过另外的主要值选择策略来提升性能.虽然MM－Cubing在数据集中执行的很好，但内存的消耗是基本表的好几倍.因此，如何提升算法的性能、减少内存的消耗以及如何更好优化生成数据立方的存储组织方式等问题是未来研究的主要方向.

［1］Beyer K，Ramakrishnan R.Bottom－up computation of sparse and iceberg cubes［C］//Delis A，Faloutsos C，Ghandeharizadeh S.SIGMOD’99.Procceedings of the 1999 ACM SIGMOD international conference on management of data，June 1－3，1999，Philadelphia，Pennsylvania.New York:ACM Press，1999，28(2): 359－370.

［2］Han J，Pei J，Dong G，et al.Efficient computation of iceberg cubes with complex measures［C］//Sellis T，Mehrotra S.SIGMOD’01.Procceedings of the 2001 ACM SIGMOD international conference on management of data，May 21－24，2001，Santa Barbara，California.New York:Association for Computing Machinery，2001，30(2):1－12.

［3］Barbara D，Sullivan M.Quasi－cubes:Exploiting approximation in multidimensional database［C］//Peckman J M.SIGMOD’97.Proceedings of 1997 ACM SIGMOD international conference on management of data，May 13－15，1997，Tucson，Arizona，USA.New York:Association for Computing Machinery，1997，26 (2):12－17.

［4］Sismanis Y，Deligiannakis A，Roussopoulos N，et al.Dwarf:Shrinking the PetaCube［C］//Franklin M，Moon B，Ailamaki A.SIGMOD’02.Proceedings of the ACM SIGMOD international conference on management of data，June 3－6，2002.New York:Association forComputing Machinery，2002，31(2): 464－475.

［5］Lakeshmanan L V S，Pei J，Han J.Quotient Cubes: How to Summarize the Semantics of a Data Cube［C］// Bressan S，Chaudhri A，Lee M L，et al.VLDB’02.Proceedings of the 28th international conference on Very Large Databases，August 20－23，2002，Hong Kong.San Fransisco:Morgan Kaufmann Publishers，2002:476－487.

［6］Shukla A，Deshpande P M，Naughton J F.Materialized view selection for multidimensional datasets［C］// VLDB’98.Proceedings of the 24th international conference on Very Large Databases，August 24－27，1998， New York.San Fransisco:Morgan Kaufmann Publishers，1998:488－499.

［7］Lakshmanan L V S，Pei J，zhao Y.QcTrees:An efficient summary structure for semantic 0LAP［C］//Halevy A Y，Ives Z G，Doan A H.SIGMOD’03.Proceedings of the ACM SIGMOD international conference on management of data，June 9－12，2003，San Diego，California.New York:Association for Computing Machinery，2003:64－75.

［8］Wang W，Feng J L，Lu H J，et al.Condensed cube:an effective approach to reducing data cube size［C］// Agrawal R，Dittrich K，Ngu A H H.ICDE’02.18th international conference on data engineering，February 26－March 1，2002，San Jose，California.Los Alamitos，California:IEEE Computer Society Press，2002: 155－165.

［9］王琢，鲍玉斌.一种快速生成最小浓缩数据立方的算法［J］.小型微型计算机系统，2005，26(12): 2212－2215.

Fast algorithm for computing condensed cube

TU Jian-xin，YOU Jin-guo
(School of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650500，China)

To generate condensed cube faster，a new approach named MM-Cubing was proposed that computes condensed cubes by factorizing the lattice space according to the frequency of values:The count and sort algorithms and related data structures were used to compute the frequency of the values，and a data structure was provided to facilitate the major value selection and compute its subspaces;the major values were selected; aggregation was operated in dense subspace and the sparse subspace was called recursivly.The result shows that MM-Cubing algorithm is significantly outperform the MinCube algorithm and SQCube algorithm.

condensed cube;lattice;space;algorithm

TP311.13

A

10.3969/j.issn.1674-2869.2012.03.011

1674-2869(2012)03-0051-05

2011-12-27

涂建新(1987－)，男，湖北黄冈人，硕士研究生.研究方向:数据仓库与并行计算.

指导老师:游进国(1977－)，男，湖南长沙人，博士，硕士生导师.研究方向:数据仓库与并行计算.

本文编辑:苗 变