基于轴对称比拟的高超声速飞行器表面热环境数值与工程耦合算法研究

代光月，桂业伟，国义军，张 勇，童福林

（中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

气动加热问题是高超声速飞行器研制与发展的最关键问题之一，准确的热环境数据是高超声速飞行器防热设计的前提。在高超声速飞行器的概念研究和初步设计阶段，工程设计需要以低成本和快速度，较为准确地预测飞行器表面的热流分布情况。因此，寻求一种快速且精度较高的高超声速气动热环境计算方法就显得非常有意义了。

一种较为简单且有效的方法是由Cooke提出，DeJarnette推广的轴对称比拟法［1］。为了采用轴对称比拟法求解热流，必须先确定表面流线形状和尺度因子，这是最困难也是极其重要的部分，直接决定着计算精度［2］。目前，基于轴对称比拟的经典流线法往往先是利用修正牛顿理论或实验等方法获得近似的表面压力，结合熵值算得其他边界层外缘参数，然后在此基础上利用简单流线法、精确流线法等方法跟踪无粘表面流线，计算尺度因子，最后利用理论和半经验公式计算出表面热流。该方法计算过程相对简单，计算速度较快，但由于需要用到压力甚至压力的二阶导数项，计算精度相对较差；它的另一个缺点是流场处理过于简单，在处理复杂外形飞行器热环境计算时往往就显得有些力不从心。国内，北京航空航天大学的康宏林［3］，西北工业大学的吕丽丽［4］和南京航空航天大学的方磊［5］等曾在此方面做过一些工作，取得了一些研究成果。

考虑到纯数值模拟虽然在直接计算热流方面还存在一些问题，但计算的压力分布是比较准确的，并且能够比较精细地刻画流场结构。本文将利用这一特点，基于轴对称比拟概念，首先利用有限体积法数值求解Euler方程获得较为准确的边界层外缘流场参数，然后基于有限元的四节点单元变换方法，直接利用笛卡尔坐标系下的三维速度分量计算无粘表面流线和尺度因子；在获取无粘表面流线和尺度因子的基础上，利用Zoby、Moss和Sutton提出的热流公式计算表面热流，从而实现数值算法和工程算法的耦合。由于该方法直接采用流场速度计算无粘表面流线，克服了经典流线法需要压力及其二阶导数且不能保证导数连续的不足，而且直接利用笛卡尔坐标系下的速度分量计算尺度因子，提高了对复杂外形的适应能力。将上述方法用于求解球锥在不同攻角条件下的表面热流，并将计算结果同经典流线法结果及实验值进行比较，从而对方法进行考核验证。

1 无粘流场的数值算法

无粘流场的数值计算部分，采用已经过多次验证、比较成熟的CFD软件平台（高超声速软件平台CHANT［6］）。直角坐标系下，无量纲化后的三维Euler方程可表述如下：

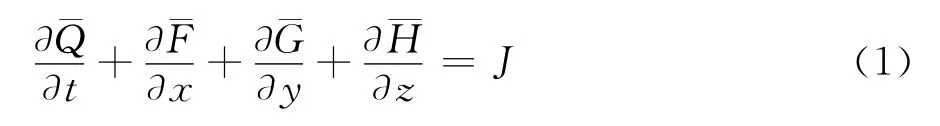
对于空间离散，本文采用一种既能保持解的单调性，又具有较高精度的NND格式［7］；而对于时间离散，采用隐式LU－SGS［8］时间推进方法。

2 流线和尺度因子的计算

2.1 表面流线的确定

在笛卡尔坐标系下，流线的定义式为：

对式（2），从某一初始位置（x0，y0，z0）积分，则可求得表面流线分布。

2.2 尺度因子的确定

空间一点（x，y，z）在笛卡尔坐标系下可写为：

若用（s，β，n）代表正交坐标系，其中s为物面上沿流线方向，β为物面上垂直于流线的方向，n为垂直物面方向，那么物面上的点可写为：

那么，垂直方向的单位矢量eβ可写为：

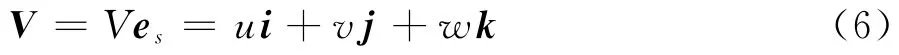
因此有

若物面外形可用F（x，y，z）＝x－x（y，z）＝0表示，则有：

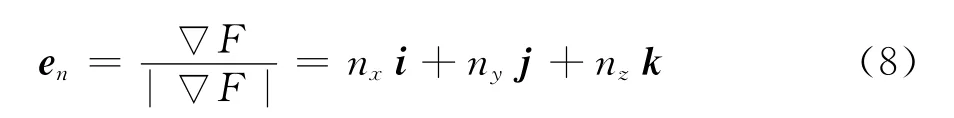
（s，β，n）为正交坐标系，即eβ＝en×es，则eβ可写为：

由式（5）和式（9）可知：

结合hβ的定义式，可知：

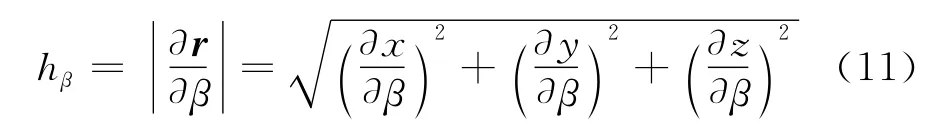
nx，ny，nz的值可利用网格坐标求出位置向量，由向量的矢量积得到。可以看到，若已知该点处的∂x／∂β，∂y／∂β，∂z／∂β，则可求出该点的尺度因子hβ，又从文献［9］可知，在物体表面有：

这样，当给定hβ一个初值，由式（10）即可求得∂x／∂β，∂y／∂β，∂z／∂β的初值，再积分式（12），即可获得沿流线的∂x／∂β，∂y／∂β，∂z／∂β，进而求得尺度因子的值。

从上面的分析可以看出，在对式（12）进行积分时，需已知（u，v，w）关于（x，y，z）的偏导数项，求解方法介绍如下［9］。

图1为一个计算单元＾Ω到物理单元Ωe的映射。通过有限元的形状函数，可以把从（ξ，η）空间到物理空间（u，v，w）的映射表示为：

图1 从计算单元＾Ω到物理单元Ωe的映射Fig.1 Mapping from master element to a physical element

对照图1可知，在计算单元每个子区域上有：

区域I

区域II

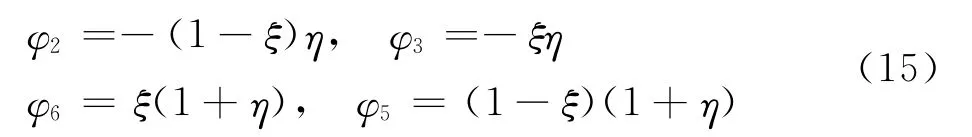
区域III

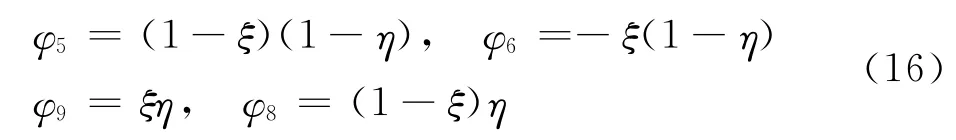
区域IV

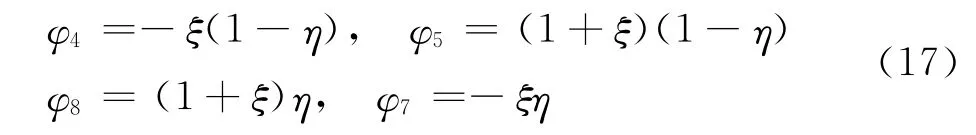
这样每个区域中关于u＝u（ξ，η）的坐标可由式（13）求得，进而可求得每个区域∂u／∂ξ，∂u／∂η，的表达式。以区域中心点处u的偏导数∂u／∂ξ，∂u／∂η为例，其值应为四个区域的平均：

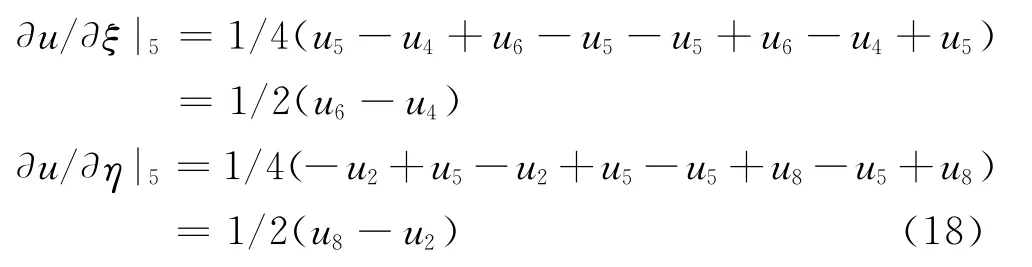
同理可以计算出v，w关于ξ，η偏导数的表达式。

同时，根据空间的映射变换关系，在进行一系列矩阵变换的基础上，可得出ξ，η关于x，y，z偏导数的表达式，以∂ξ／∂x为例：

其中｜J｜是转换的Jacobian行列式，数值上为物理单元与计算单元的面积比，表达式为：

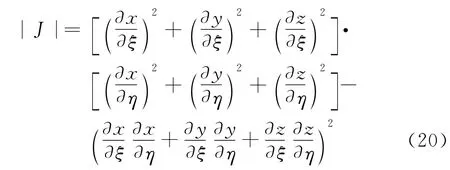
又因（u，v，w）关于（x，y，z）的偏导数具有如下表达式，以u为例：

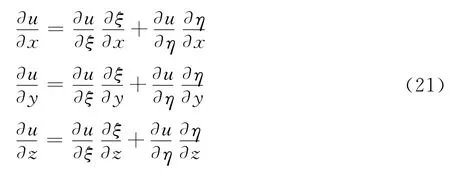
这样，（u，v，w）关于（x，y，z）偏导数项的值就可以求得了。

2.3 逆向跟踪流线

上述方法可用于逆向跟踪流线，只需在式（2）的右边加一负号即可，这样，对于任意一个想要考察其热量值的特定点，都可以通过指定该点为起始点的方式直接求出该点的热流值，而不需要插值附近点获得；同时，还大大方便了表面流线的布置，特别是在有攻角情况下，由于流线向背风区汇集，传统方法很难使流线均匀覆盖飞行器表面，而利用逆向跟踪流线，可使流线分布的十分均匀。

3 高超声速热流计算

3.1 驻点热流计算

本文采用经典的Fay－Riddell公式［1］计算驻点热流，并将其与实验测得的热流值进行比较。Fay－Riddell公式的表达式为：

3.2 非驻点热流计算

对于非驻点区域绕流，本文选取了由Zoby，Moss和Sutton等提出的应用广泛且具有较好精度的热流计算公式［10］。层流热流的计算公式为：

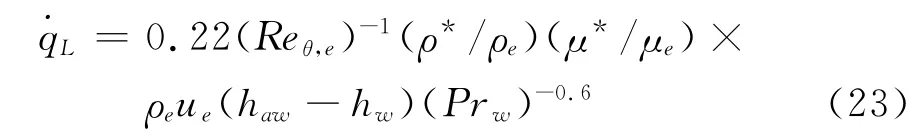
湍流热流的计算公式为：

其中，Reθ，e是基于边界层动量厚度的雷诺数，边界层动量厚度θ的表达式分别为：

式（25）中，h为尺度因子，s为沿流线的长度。

4 方法验证

4.1 计算条件

本文选择了有详尽实验数据的三维球锥绕流问题进行计算，以达到对方法进行考核验证的目的。计算所用模型的具体尺寸为：头部曲率半径为3.835mm，半锥角为12.84°，锥尾距头部距离为69.55mm。在单纯有攻角情况下，由于流场左右对称，取半流场进行计算，来流参数值与实验数据对应工况［11］相一致：p∞＝61Pa，T∞＝49.8K，Ma∞＝9.86。网格类型为单块结构网格。通过网格实验，兼顾计算精度与计算效率，网格数为39×41×31。计算时，取攻角分别为0°、8°和16°。

4.2 无粘流场结果分析

图2是球锥在攻角分别为0°、8°和16°时球锥表面压力分布云图。由图可以看出，由于来流马赫数较高，在球锥的头部，产生了一道很强的头激波，波后存在一个较强的高压区，随着计算攻角的增大，迎风面的压力值逐渐增大，流场结构清晰，符合物理规律。

4.3 流线分析

图3是球锥在攻角分别为0°、8°和16°时的壁面流线分布图。可以看出，流线形状随着攻角增大而扭曲，攻角越大，扭曲程度越厉害，向背风区汇集，壁面流线分布情况较好，符合实际物理情况。

图2 攻角为0°、8°和16°时球锥表面压力分布云图Fig.2 Pressure distribution of conic，forα＝0°，8°and 16°

图3 球锥在攻角分别为0°、8°和16°时的壁面流线分布图Fig.3 Surface streamlines of conic，forα＝0°，8°and 16°

4.4 驻点区域热流计算结果分析

高超声速飞行器的驻点加热非常重要，它是最具代表性的点。同时，为了将算得的热流密度值进行归一化处理，便于比较，也需首先求出驻点热流值。本文采取经典的Fay－Riddell公式计算驻点热流，并将其与实验测得的热流值进行比较，结果见下表。

表1 不同攻角下球锥驻点热流值比较Table 1 Comparison of heating rates at stagnation point

从上表可以看出，计算出的热流值与实验值吻合的较好，因此，本文计算得出的热流密度值是符合物理规律，可用的。

4.5 非驻点区域热流计算结果分析

图4是球锥在攻角分别为0°、8°和16°时的迎风子午线上的热流分布示意图，图5是球锥在8°攻角时背风子午线上的热流分布示意图。L是参考长度，即：锥尾距头部距离；图中热流密度值为进行归一化后的热流值。从图中可以看出：无论是有攻角还是无攻角条件，迎风和背风子午线上热流计算结果与实验值均吻合的较好，计算精度较经典工程算法有较大提高。

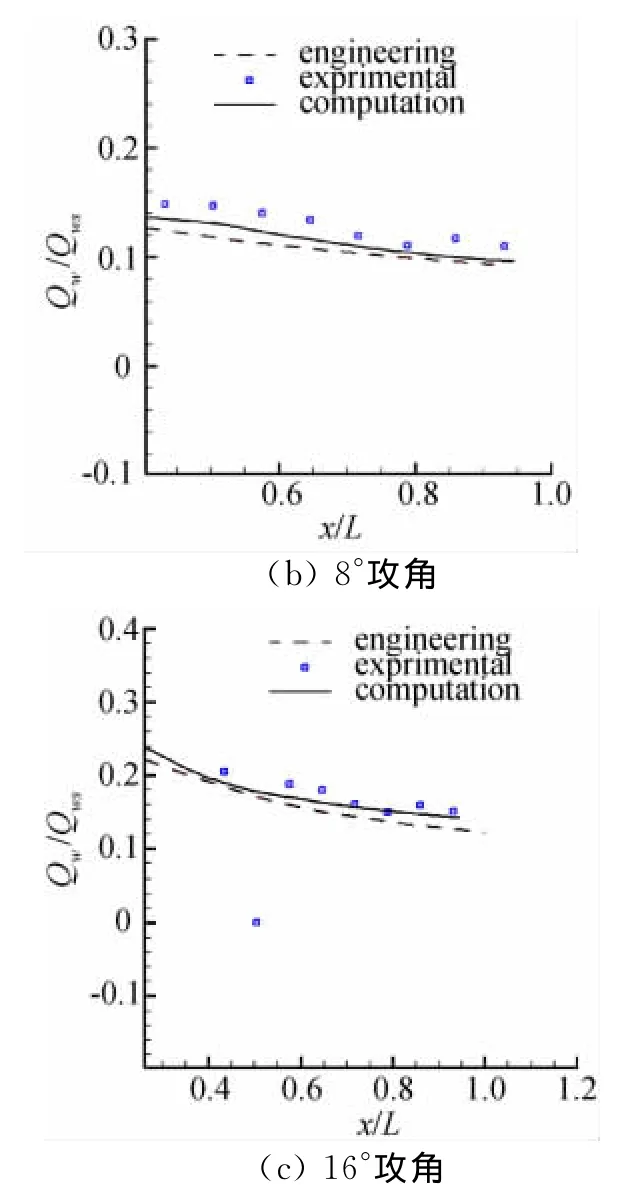
图4 球锥在攻角分别为0°、8°和16°时的迎风子午线上的热流分布示意图Fig.4 Windward centerline heating rate distribution，forα＝0°，8°and 16°

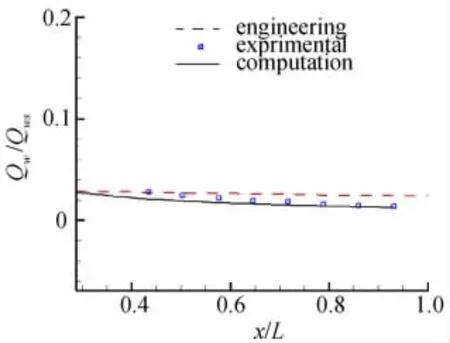
图5 球锥8°时的背风子午线上的热流分布示意图Fig.5 leeward centerline heating rate distribution

5 结束语

基于轴对称比拟，将数值算法和工程算法耦合起来，利用有限体积法数值求解Euler方程获得较为准确的边界层外缘无粘流场参数，然后基于有限元的四节点单元变换方法，直接利用笛卡尔坐标系下的三维速度分量计算无粘表面流线和尺度因子；在获取无粘表面流线和尺度因子的基础上，利用Zoby、Moss和Sutton提出的热流公式计算表面热流。该方法直接采用流场速度计算无粘表面流线，克服了经典流线法需要压力及其二阶导数且不能保证导数连续的不足，而且直接利用笛卡尔坐标系下的速度分量计算尺度因子，提高了对复杂外形的适应能力。为了对方法进行考核验证，将上述方法用于求解球锥在不同攻角条件下的表面热流分布情况，将计算结果同经典流线法结果和实验值进行对比，结果表明：本文计算结果与实验值吻合的较好，计算精度较经典工程算法有较大提高。将程序进一步完善，使其适用于多块结构网格和对高精度网格技术的探讨将是下一步研究的重点。

［1］中国人民解放军总装备部军事训练教材编辑工作委员会.高超声速气动热和热防护［M］.北京：国防工业出版社，2003.

［2］HAMILTON H H，WEILMUENSTER K J.Application of axisymmetric analogue for calculating heating in threedimensional flows［A］.AIAA 23rd Aerospace Sciences Meeting［C］.January，1985.

［3］康宏琳，阎超，李亭鹤，等.高超声速再入钝头体表面热流计算［J］.北京航空航天大学学报，2006，32（12）：1395－1398.

［4］吕丽丽.高超声速气动热工程算法研究［D］.［硕士学位论文］.西北工业大学，2005.

［5］方磊.基于流线跟踪法的气动热工程计算研究［D］.［硕士学位论文］.南京航空航天大学，2008.

［6］中国空气动力研究与发展中心计算空气动力学研究所高超声速研究室.高超CFD平台0.0版［M］.2003.

［7］张涵信.无波动、无自由参数的耗散差分格式［J］.空气动力学学报，1988，6：143－164.

［8］SHAROV D，NAKAHASHI K.Reordering of 3Dhybrid unstrucrured grids for vectorized LU－SGS navierstokes computations［R］.AIAA－97－2102.

［9］WANG K C.An axisymmetric analog two－layer convective heating procedure with application to the evaluation of space shuttle orbiter wing leading edge and windward surface heating［R］.NASA C R 188343，1994.

［10］ZOBY E V，MOSS J N，SUTTON K.Approximate convective heating equations for hypersonic flows［J］.Journal of Spacecraft and Rockets，1981，18（1）.

［11］MILLER C G.Experimental and predicted heating distributions for biconics at incidence in air at Mach 10［R］.NASA－TP－2334，1984.