异型建筑物年预计雷击次数计算

李景水

(山西省建筑设计研究院，山西 太原 030013)

1 概述

在GB 50057-2010建筑物防雷设计规范中，作为强制性条文，从3.0.2条到3.0.4条规定了建筑物防雷要求分类方法。作为其中重要的分类依据，必须准确计算建筑物的年预计雷击次数。特别是当建筑物的预计雷击次数计算值临近0.05次/年和0.25次/年等分界值时，精确的计算对防雷分类的准确性尤为重要。

实际工程中建筑物的形状大多比较复杂，如图1所示的建筑物，严格按实际形状计算比较复杂，需要简化计算，但多大的凸、凹部分可以忽略，多大的应该计算，在规范和各种资料中都没有量化的规定，实际工程中一般由工程设计人员凭经验确定。

图1 复杂形状建筑物示意图（一）

经过对各种体型的建筑，不同大小的凸、凹部分进行计算分析，本文分析了凸、凹部分可以忽略不计的具体条件，以及需要计算时的计算方法。

2 建筑物年预计雷击次数计算方法

在《建筑物防雷设计规范》附录A建筑物年预计雷击次数一节中，仅给出了标准矩形建筑物的年预计雷击次数的计算公式:

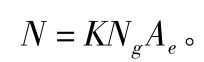
其中，K为校正系数;Ng为建筑物所处地区雷击大地的年平均密度;Ae为建筑物接收相同雷击次数的等效面积。Ae=[LW+2D(L+W)+πD2]×10－6;其中，L，W，D 分别为矩形建筑物的长、宽、每边的扩大宽度，当建筑物的高H＜100 m时，其每边的扩大宽度D2=H(200－H)，当建筑物的高H≥100 m时，其每边的扩大宽度D=H。

当建筑物形状复杂时，需根据GB 50057-2010建筑物防雷设计规范第A.0.3条第7款，应沿建筑物周边逐点算出最大扩大宽度，其等效面积应按每点最大扩大宽度外端的连接线所包围的面积计算。如图2所示，有凹槽时，实际面积为按标准矩形计算的面积减去图中阴影部分的误差面积。

图2 复杂形状建筑物示意图（二）

我们根据以下几种情况，分别分析不同形状的建筑物Ae的简化计算方法。

3 矩形建筑物中间有凹槽时年预计雷击次数计算

某建筑物长L=100 m;宽W=40 m;校正系数K=1;年平均雷暴日数按太原市资料取34.5(雷击大地的年平均密度Ng=0.1×34.5=3.45);建筑中间有一凹槽长 La=1/2L=50 m;宽 Wa=1/2W=20 m;在不同建筑物高度时计算出等效面积Ae和年预计雷击次数N分别见表1。

由表1的结果可知，建筑物中间有凹槽时，凹槽长宽均为建筑长宽的1/2，且预计雷击次数计算值临近0.05次/年分界值时，实际计算结果和不计凹槽影响时的简化计算值都可以约等于0.050次/年，对防雷分类没有影响。通过计算机程序建立模型，对建筑长度在5 m～1 000 m，宽度在5 m～1 000 m，高度在3 m～100 m，数千个不同大小的建筑物模型进行数据分析，得出矩形建筑物中间有凹槽时简化处理方法:

简化方法1:

矩形建筑物中间有凹槽时，当凹槽的长度La小于扩大宽度D时，不管凹槽的深度是大是小，凹槽对矩形建筑物的年预计雷击次数计算结果的影响都很小，误差均小于1%，可以忽略不计;D＜La＜2D时，当对计算结果精度要求不高时，也可以忽略不计;当凹槽的长度La大于2倍扩大宽度D时，凹槽对矩形建筑物的年预计雷击次数计算结果的影响已经比较大，须计算其影响。

表1 凹槽对矩形建筑物的年预计雷击次数计算结果的影响(一)

如图3所示，D和La，Wa相对大小不同时，误差面积的形状也各不相同，计算应分为两种情况(其中Ae为计算等效面积;Aeo为标准矩形建筑物的等效面积;建筑物长L、宽W、凹槽长La、宽Wa):

当L2a+4W2a－8D×Wa＞0时:Ae=Aeo+α×D2+(D×Wa－D2)×sinα －La×Wa。

公式中α=arccos(1－Wa/D)。

当L2a+4Wa2－8D ×Wa≤0时:Ae=Aeo+α×D2+0.5La×D×cosα－La×D。

公式中 α=arcsin(0.5×La/D)。

计算公式虽然比较复杂，但利用Excel等计算机软件，可以很容易得到精确的结果。

4 矩形建筑物四角有凹槽时年预计雷击次数计算

某建筑物长L=100 m;宽W=40 m;校正系数K=1;雷击大地的年平均密度Ng=3.45;建筑左上角有一凹槽长La=1/4L=25 m;宽Wa=1/4W=10 m;在不同建筑物高度时计算出等效面积Ae和年预计雷击次数N分别见表2。

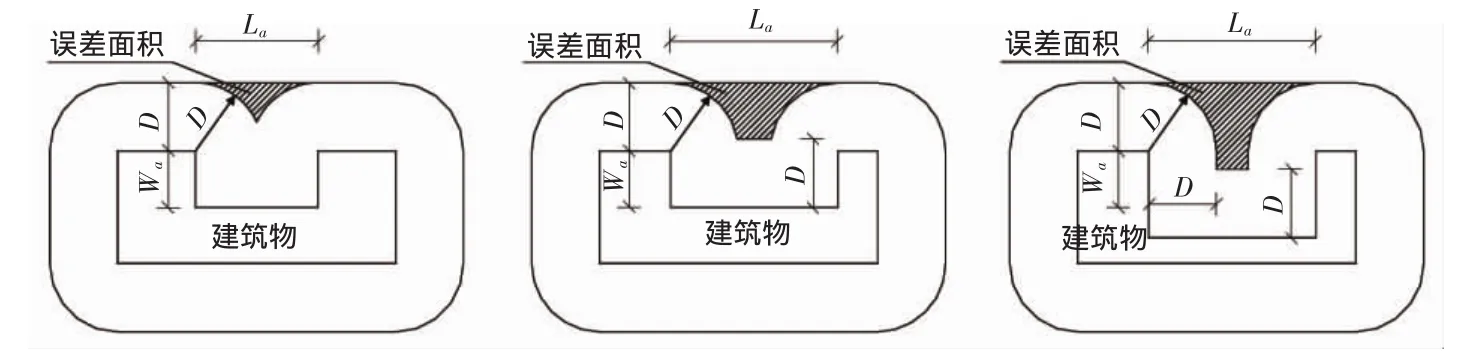
图3 复杂形状建筑物示意图（三）

表2 凹槽对矩形建筑物的年预计雷击次数计算结果的影响(二)

由表2的结果可知，建筑物四角有凹槽时，凹槽长宽均为建筑长宽的1/4，且预计雷击次数计算值临近0.05次/年分界值时，实际计算结果约等于0.049次/年，不计凹槽影响时的简化计算值约等于0.050次/年，对防雷分类己经有影响。

通过计算机程序建立数据库，对建筑长度在5 m～1 000 m，宽度在5 m～1 000 m，高度在3 m～100 m的数千个不同大小的建筑物进行数据分析，得出矩形建筑物四角有凹槽时的简化处理方法。

简化方法2:

矩形建筑物四角有凹槽时，在凹槽的长宽分别小于矩形建筑物的1/8，并且长宽均小于0.5D时，凹槽对矩形建筑物的年预计雷击次数计算结果的影响小于1%，可以忽略不计。当须计算四角凹槽对矩形建筑物的年预计雷击次数计算结果的影响时，可以按以下公式计算(计算时应取La＞Wa):

当Wa＜D时:Ae=Aeo+0.5α ×D2－0.5×(D－Wa)×D ×sinα －(D+La)×Wa。

其中，α=arccos(1－Wa/D)。

当 Wa≥D 时:Ae=Aeo+0.25πD2+Wa×La+D ×(D －2Wa－2La)。

5 矩形建筑物有凸起时年预计雷击次数计算

矩形建筑有凸起时，可以转化计算方式，将有凸起建筑物，转化为一个较大的矩形建筑物，其两个角或一角有凹槽，通过以上三、四项的方法进行分析计算。

其简化处理方法如下:

简化方法3:

建筑物边的中部有凸起时，在凸起长宽小于建筑物长宽的1/10并且小于D时，误差一般小于1%，可以忽略不计;当建筑物凸起移至四角时，在凸起长宽比例小于建筑物的1/20并且小于D的1/2时，误差一般小于1%，可以忽略不计。当须计算时，可以转化为计算凹槽，按以上三、四项的方法进行计算。

6 复杂形状建筑物简化实例

如图1中的建筑物，较小的凹槽、凸起在满足以上简化方法1～方法3中可以忽略的条件时，可以转化为一个标准的矩形建筑。对于图1中L形建筑和T形建筑，可以通过将其转化为一个角或两个角有凹槽的矩形建筑物，通过简化方法1，方法2的公式来进行计算。

对更复杂的建筑，也可以通过先将其较小的凹槽、凸起，在满足简化方法1～方法3中可以忽略的条件时，先简化掉，然后转化为一个有较少的凹槽的基本矩形建筑，再通过简化方法1，方法2的公式来进行计算。

当建筑平面复杂，各部分高度不同时，计算就不再是最好的方法，通过绘图的方式更为合理。绘图时，建筑中较小的凸凹在满足以上条件时可以忽略，既能简化绘图的工作量，也可以得到正确的结果。

[1] GB 50057-2010，建筑物防雷设计规范[S].