中间主应力对垂直井井壁坍塌压力的影响

梁 涛，杨甘生，雷 静

(中国地质大学〈北京〉科学钻探国家专业实验室，北京 100083)

中间主应力对垂直井井壁坍塌压力的影响

梁 涛，杨甘生，雷 静

(中国地质大学〈北京〉科学钻探国家专业实验室，北京 100083)

运用线弹性本构模型来分析垂直井井壁应力分布，并分别用Mohr-Coulomb准则、Drucker-Prager准则和Mogi-Coulomb准则3个强度准则来计算平谷地应力测量与监测钻孔维持井壁稳定所需的最小钻井液液柱压力。通过对比分析得出考虑中间主应力的作用，会使岩石强度得到加强，使得维持井壁稳定所需的最小液柱压力降低;3个准则得出的最小液柱压力在与深度的对应图中表现出一致的变化趋势，说明3个准则有各自的适用性;比较而言Mohr-Coulomb准则偏于保守，Drucker-Prager准则偏于危险，而Mogi-Coulomb准则要优于前两个准则。

中间主应力;强度准则;最小液柱压力

0 前言

井壁坍塌是钻井过程中遇到的最主要的井壁稳定问题之一。井壁坍塌是在井眼钻开后，由于原地应力的作用，导致井壁处发生应力集中，井围岩所承受的应力超过了自身强度而发生失稳［1］。最主要的解决方法是确定合理的钻井液密度，来改善井壁围岩的应力集中现象，保持井壁稳定。确定合理的钻井液密度，需要一个本构模型来确定井壁围岩的应力分布，以及一个强度准则来确定围岩的极限强度。本文采用线弹性各向同性的本构模型来确定井围岩的应力分布，通过选用不同的强度准则来分析中间主应力对维持井壁稳定的最小钻井液液柱压力的影响以及各破坏准则的适用性。

Mohr-Coulomb准则是目前应用最广泛的破坏准则，该准则认为中间主应力对岩石强度没有影响。但中间主应力对岩石强度影响已经被证明，中间主应力可以使岩石强度得到加强［2～5］。为了得到中间主应力对岩石强度的影响，很多三维的强度准则被建立。但很多三维强度准则由于参数较多且很多参数不易得到，应用起来比较困难。Drucker-Prager准则是比较常用的三维强度准则，它只包含2个参数，且这2个参数只与岩石的内摩擦角和粘聚力有关。但有文献指出，Drucker-Prager强度准则过高的估计了中间主应力对岩石强度的影响，从而导致稳定性预测结果偏于危险［6～9］。Mogi-Coulomb准则是在2005年由Al-Ajmi和Zimmerman提出的一个考虑中主应力的三维强度准则［10］。Mogi-Coulomb准则只包含2个参数，直接与内摩擦角及粘聚力相关。

1 垂直井井壁围岩应力分析

深部地层通常受一个垂向地应力和2个水平向地应力及孔隙压力的共同作用。井眼形成后破坏了原地应力的平衡状态，造成井壁围岩应力的重新分布，产生应力集中。当井眼钻达低强度地层时，应力集中可能造成井壁围岩破坏，即井壁失稳。在井壁稳定性分析中，井壁处的应力必须通过强度准则进行校核。垂直井井壁处的应力可以由下式给出［11］:

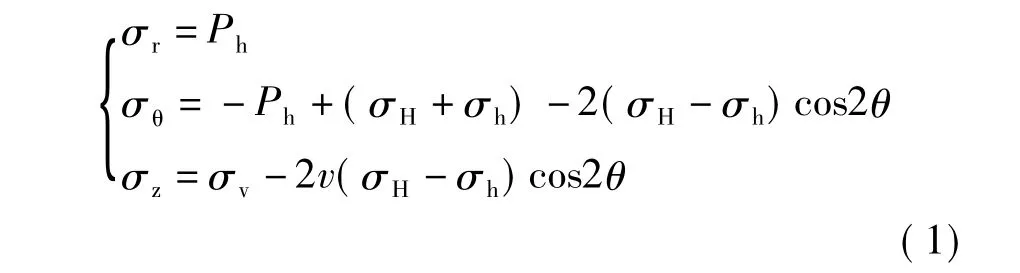
式中:Ph——钻井液液柱压力;σv——上覆岩层压力;σH——最大水平地应力;σh——最小水平地应力;v——泊松比;θ——井周方位角。

由式(1)可知切应力为零，σθ、σz和σr可以直接作为主应力代入强度准则。

从式(1)可以看出，周向应力和轴向应力都是井周方位角θ的函数，θ在0～2π之间变化。很显然，当θ=±π/2时周向应力和径向应力同时达到最大值，当θ=0或π时二者同时达到最小值。而且无论井壁应力维持在什么水平，井壁发生破坏的位置不会改变。

由式(1)还可以知道，周向应力和径向应力同时也是钻井液柱压力Ph的函数，因此钻井液压力的改变将引起σθ和σr的变化。我们知道井壁坍塌是由于受到压应力作用而造成的剪切破坏，当钻井液柱压力Ph减小时，周向应力σθ增大且为压应力。此时σθ≥σr，但3个主应力的大小顺序存在3种可能:(1)σz≥σθ≥σr;(2)σθ≥σz≥σr;(3)σθ≥σr≥σz。当σθ达最大值时θ=±π/2，此时3个主应力值为:

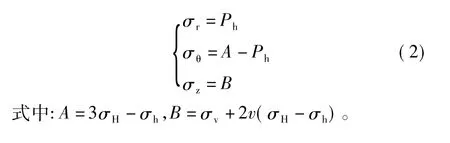
2 岩石的强度准则

2.1 Mohr-Coulomb准则

Mohr-Coulomb准则是由莫尔(Mohr)和库伦(Coulomb)提出的，它认为当材料在某平面上剪应力τn达到某一特定值时，就发生破坏，这与金属材料的Tesca准则不同，这一特定值与平面上的正应力σn有关，可以表示为:

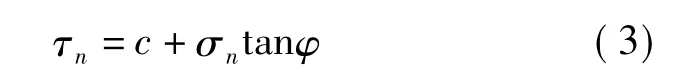
式中:c——材料的粘聚力;φ——材料的内摩擦角。

式(3)是可以用最大切应力τmax和有效平均应力σm，2表示:

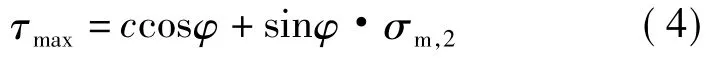
式中:τmax=(σ1－σ2)/2，σm，2=(σ1+σ3)/2。

该准则还可以用最大、最小主应力σ1和σ3的形式表示:

式中:C0=2ccosφ/(1－sinφ)，q=tan(π/4+φ/2)。

2.2 Drucker-Prager准则

Drucker-Prager准则是在Mohr-Coulomb准则和塑性力学中著名的Mises准则的基础上拓展和推广而得，最初应用于土力学［12、13］。它的表达式如下:

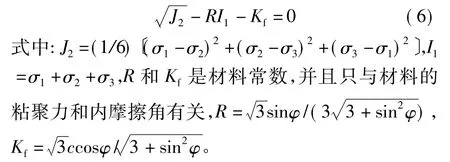
2.3 Mogi-Coulomb准则

Mogi在研究脆性岩石压裂破坏时发现，岩石的破坏面总是沿着中间主应力σ2方向，同时他还发现中间主应力使岩石强度加强［14］。因此Mogi提出了一个新的强度准则:

由于函数的非线性关系，导致关系式中的参数很难求得。为了解决这一问题Al-Ajmi和Zimmerman［7］将f作为线性关系来考虑，得到强度准则的表达式为:

由式(4)和(8)可知当σ1=σ2时，Mogi准则退化为Mohr-Coulomb准则，Mogi准则是Mohr-Coulomb准则的推广，因此该准则称为Mogi-Coulomb准则。由此可以得到式中参数［15］:

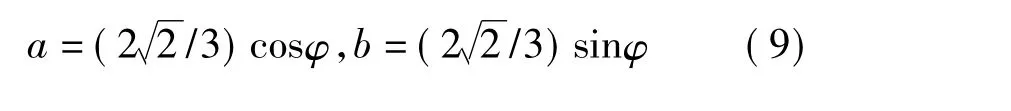
3 维持井壁稳定的最小钻井液液柱压力计算

3.1 Mohr-Coulomb准则

当考虑有效应力的概念时，Mohr-Coulomb准则表达式如下:

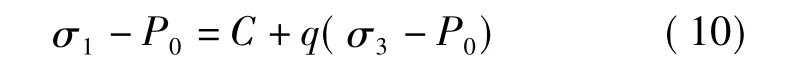
式中:P0——地层空隙压力。

改变式(1)的形式，该式可以变为:

式中:C=C0－P0(q－1)。

考虑井壁坍塌时应力分布的第一种情况σz≥ σθ≥σr，此时σ1=σz并且σ3=σr。将式(2)代入式(11)，可以得到与第一种情况相对应的维持井壁稳定的最小钻井液液柱压力，表达式如下:

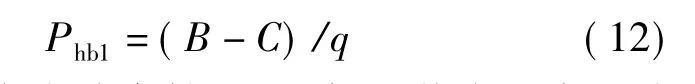
在第一种应力分布情况下，如果井内的实际液柱压力低于Phb1，井壁将发生坍塌。用同样的方法可以得到其他2种情况下的最小钻井液液柱压力表达式，如表1所示。

表1 Mohr-Coulomb准则得到的最小液柱压力表达式

将计算得到的3个最小液柱压力，代回到式(2)中反算主应力(σz，σθ，σr)，并将计算出的主应力代入式(11)，满足Mohr-Coulomb准则的即为真正的最小液柱压力。

3.2 Drucker-Prager准则

根据第一和第二应力不变量的定义可知:

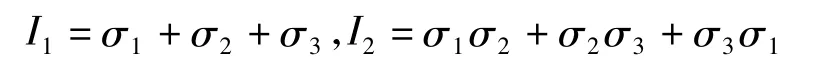
由式(2)可知上式可以变换为:

并且考虑有效应力的概念，Drucker-Prager准则可以改写为如下形式:

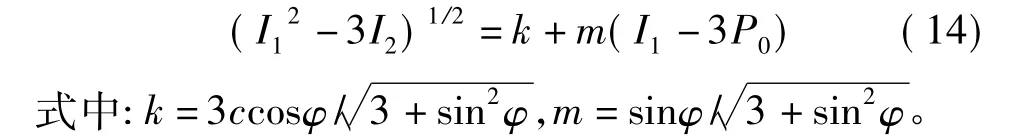
将式(13)代入式(14)即可求出Phb，观察式(14)发现3个主应力总是同时出现，无论主应力的大小如何排列表达式只用一种情况，因此可以求得唯一的最小液柱压力。

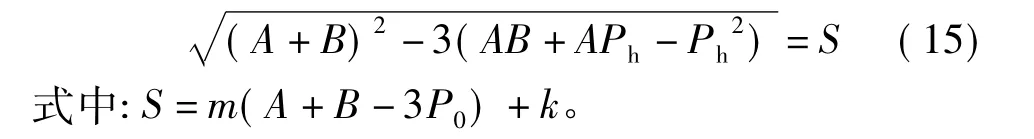
由式(15)可以解得2个Phb，在此讨论的是井壁坍塌的情况，因此较小的根是我们要求的最小液柱压力。

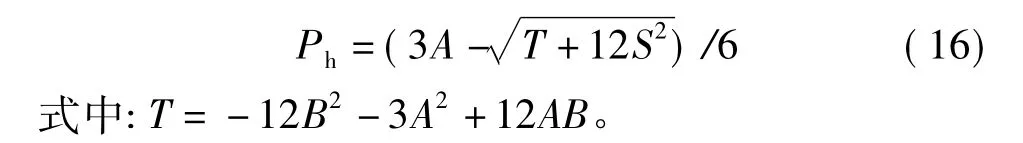
3.3 Mogi-Coulomb准则

与Drucker-Prager准则类似，Mogi-Coulomb准则可以改写为:

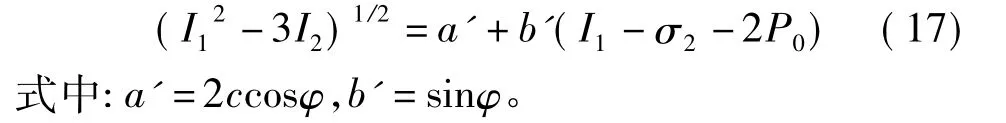
从式(17)中可以看出，随着σ2的不同，表达式也不同，因此对应着上述的3种情况，这里讨论第一种情况，即σz≥σθ≥σr。此时σ2=A－Ph，将式(2)和式(13)代入式(17)得:

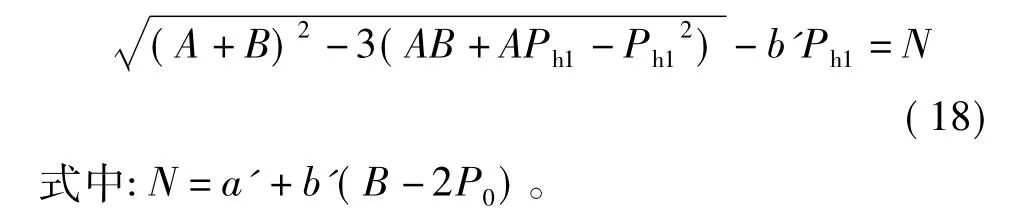
解式(18)可以得到第一种情况下，所需的最小液柱压力表达式如下:

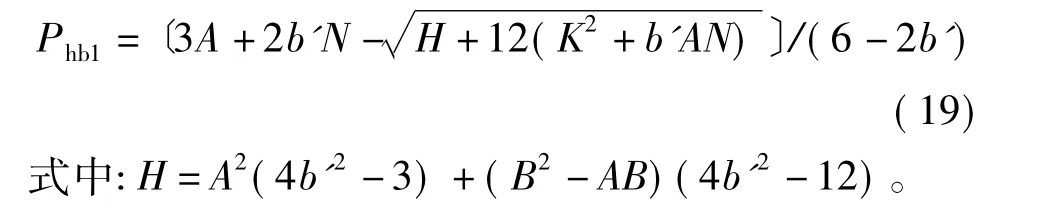
同理可以得到其余2种情况下的最小液柱压力的表达式，见表2。

表2 Mogi-Coulomb准则得到的垂直井井壁坍塌压力

与Mohr-Coulomb准则一样，计算出的最小液柱压力需要通过式(2)反算3个主应力，并将求得的主应力值代入式(17)，满足式(17)的即为所求的最小液柱压力。

4 工程实例分析

平谷地应力测量与监测钻孔位于北京市平谷区独乐河镇南山村盘山花岗岩体，由北京市地质工程设计研究院设计施工，用于北京地区主要活动断裂工程地质稳定性评价与地应力测量，共完成了600.47 m钻探工作。钻探所取岩心表明，所选地应力测量点处的岩石主要由花岗岩和灰岩组成，其中孔口至413.13 m为花岗岩，413.13～600.47 m由灰岩和花岗岩组成。花岗岩岩层中，孔口至54.56 m间为风化带，54.56 m以下花岗岩，除局部夹有破碎带外，岩石基本未受风化;灰岩岩层中，岩石遭受接触变质作用，岩石完整，局部夹有薄层矿化带。

现场根据岩心的完整性及水压致裂法地应力测量的要求，进行了26个不同深度地应力大小测量，最终获取22个不同深度地应力大小测量有效结果。为了较少地形地貌对原地应力的影响，本文只研究300 m以下井段，地应力测量成果如表3所示。

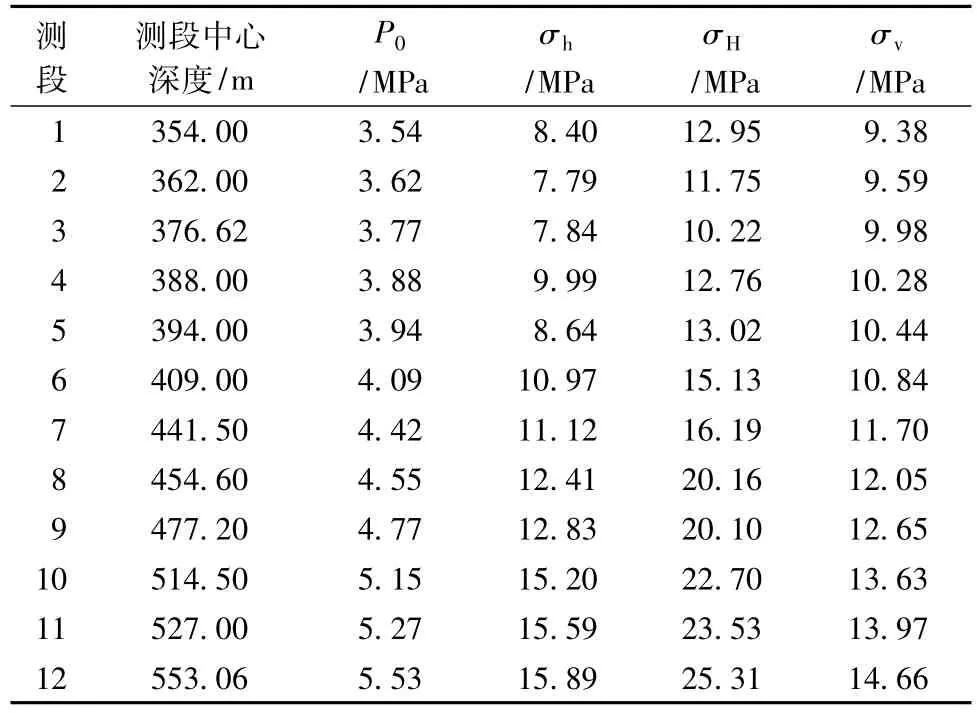
表3 平谷钻孔地应力测量成果

该孔在地应力测量井段均采取了岩心，并对岩心做了相应的岩石力学实验，成果如表4所示。

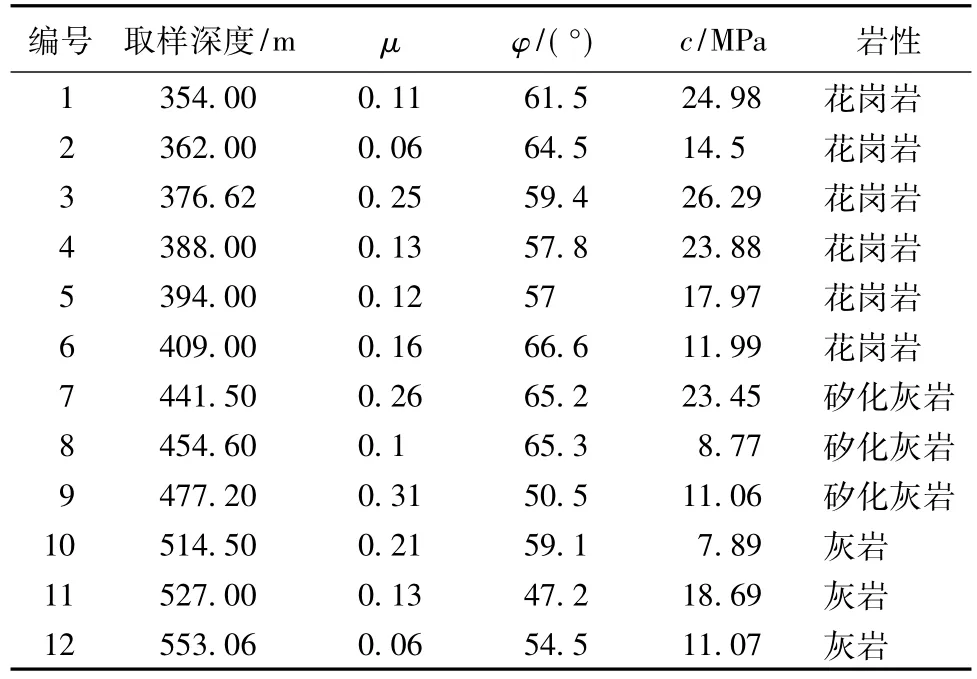
表4 平谷钻孔岩石力学实验成果

根据前述的3个岩石强度准则，以及平谷钻孔的地应力测量和岩石力学实验成果，可以分别求出该孔实验井段保持井壁稳定的最小钻井液液柱压力(见表5)。

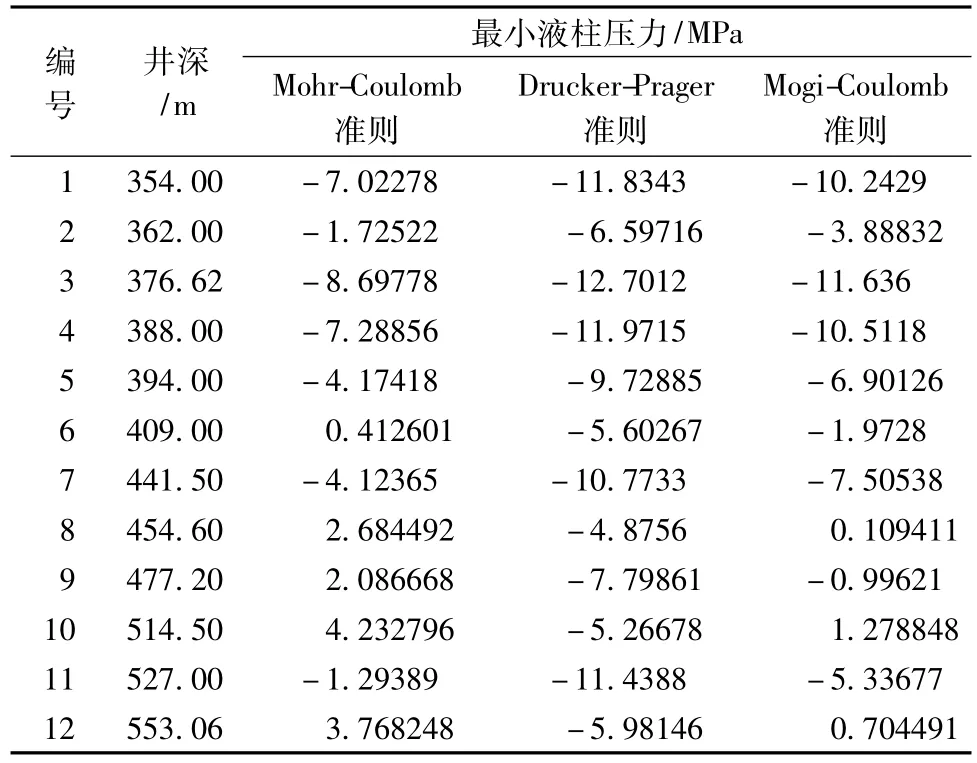
表5 三个准则求得的平谷钻孔各井段所需的最小液柱压力

从表5中可以看到，所求得的最小液柱压力大部分为负值，这是因为所钻地层的孔隙压力较小，且地层较完整、井壁围岩强度较高。实际钻井过程中，基本上采用清水钻进，很好的说明了地层的完整性及稳定性。从表5中很难看出3个准则之间的对比关系，因此我们绘制各个准则最小液柱压力与深度的对应关系图(见图1)。

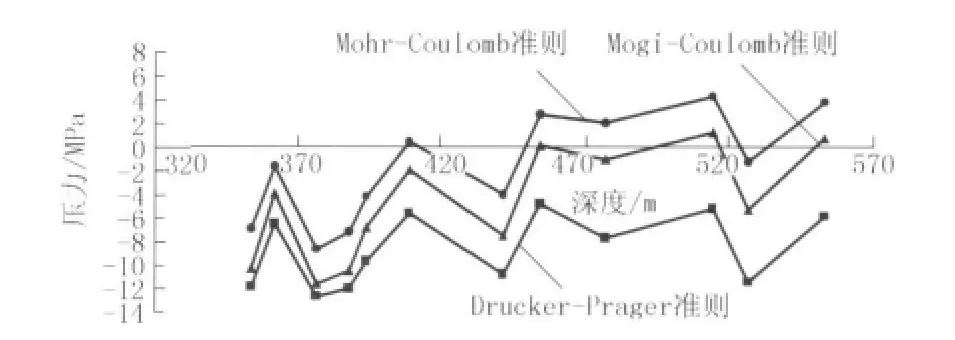
图1 三准则求得最小液柱压力与深度对应图

由图1可知，3个准则所求得的最小液柱压力随着深度的变化规律是一致的，这说明3个准则在解决井壁坍塌稳定的方面都具有一定的适应性。其中Mohr-Coulomb准则得出的维持井壁稳定的最小液柱压力是最大的，这与目前普遍的认识相一致，Mohr-Coulomb准则没有考虑中间主应力对岩石强度的贡献，因而偏于保守;Drucker-Prager准则得出的维持井壁稳定的最小液柱压力是最小的，这是因为它考虑了中间主应力对岩石强度的贡献，且在表达式中全面的体现出来，但如前所述有文献指出该准则过高的估计了中间主应力对岩石强度的贡献，从而使预测值偏于危险;Mogi-Coulomb准则得出的维持井壁稳定的最小液柱压力位于前2个准则之间，这说明该准则不仅考虑了中间主应力的影响，而且合理的估计了中间主应力对岩石强度的贡献，因此较于前2个准则更趋于合理。实际钻进过程中井壁稳定情况也很好的说明了上述结果，尤其在450～520 m局部井段岩心较破碎，并没有 Drucker-Prager准则所表现出的高稳定性，但用清水钻进也没有发生严重的井壁坍塌问题，因此也没有Mohr-Coulomb准则所有预测的那样危险。

在图1还可以看到，在不同的岩性中3个准则所表现出的差异性也不同。在花岗岩中3个准则的差异性较小，得出的最小液柱压力较接近，而随着岩性的变化到灰岩中差异逐渐变大。强度准则对不同岩性的适用性也是不同的，在选取强度准则时要充分考虑这一问题。

5 结论

(1)Mohr-Coulomb准则、Drucker-Prager准则和Mogi-Coulomb准则在解决井壁坍塌稳定问题上，表现出一致的变化规律，都具有一定的适用性。

(2)Mohr-Coulomb准则和Drucker-Prager准则一个偏于保守，一个偏于危险，而Mogi-Coulomb准则介于二者之间较为合理。

(3)通过3个准则的对比可知，中间主应力对岩石强度起到很好的加强作用，从而使维持井壁稳定所需的最小液柱压力减小。但中间主应力对岩石强度的加强作用也是有限的，过高的估计中间主应力的作用是危险的。

(4)强度准则对不同岩性的适用性也是不同的，本文没有对强度准则对不同岩石的适用性做更多的探讨，有待于日后做更深入的研究。

［1］刘玉石.地层坍塌压力及井壁稳定预测研究［J］.岩石力学与工程学报，2004，23(14):2421－2423.

［2］方开泽.土的破坏准则——考虑中主应力的影响［J］.华东水利学院学报，1986，14(2):70－81.

［3］Hoskins ER.The failure of thick-walled hollow cylinders of isotropic rock［J］.Int J Rock Mech Min Sci Geomech Abstr，1969，6 (1):99－116.

［4］Haimson BC，Chang C.A new true triaxial cell for testing mechanical properties of rock，and its use to determine rock strength and deformability of westerly granite［J］.Int J Rock Mech Min Sci，2000，37:285－296.

［5］李晓春，许东俊.中间主应力对岩石强度的影响程度和规律［J］.岩石力学与工程学报，1991，12(1):9－16.

［6］Ewy RT.Wellbore-stability prediction by use of a modified Lade criterion［J］.SPE Drill＆Complet，1999，14(2):85－91.

［7］McLean M，Addis M.Wellbore stability:the effect of strength criterion on mud weight recommendations［C］.In:proceedings of the 65th annual technical conference and exhibition［A］，New Orleans:Society of petroleum engineers，1990:SPE，20405.

［8］赵春风，杨砚宗，张常光，等.考虑中主应力的常用破坏准则适用性研究［J］.岩石力学与工程学报，2011，30(2):327－334.

［9］俞茂宏.岩土类材料的统一强度理论及其应用［J］.岩土工程学报，1994，16(2):1－9.

［10］A.M Al-Ajmi，R.W.Zimmerman.Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion［J］.International Journal of Rock Mechanics＆Mining Sciences，2006，43: 1200－1211.

［11］邓金根.井壁稳定预测技术［M］.北京:石油工业出版社，2008.33－38.

［12］王建军.岩石破坏德鲁克—普拉格准则的探讨［J］.科技信息，2009，(7):686.

［13］Drucker DC，Prager W.Soil mechanics and plastic analysis or limit design［J］.Quart Appl Math，1952，(10):157－165.

［14］Mogi K.Fracture and flow of rock under high triaxial compression.J Geophys Res，1971，76(5):1255－1269.

［15］A.M Al-Ajmi，R.W.Zimmerman.Relationship between the parameters of the Mogi and Coulomb failure criterion［J］.Int J Rock Mech Min Sci，2005，42(3):431－439.

Effect of Intermediate Principal Stress on the Wall Collapsing Pressure of Vertical Wellbore

LIANG Tao，YANG Gan-sheng，LEI Jing(State Professional Lab of Scientific Drilling，China University of Geosciences，Beijing 100083，China)

Linear elastic constitutive model was used to analyze the stress distribution in the vertical wellbore;Mohr-Coulomb criterion，Drucker-Prager criterion and Mogi-Coulomb strength criterion were respectively applied to calculate the minimum fluid column pressure required to maintain stable wellbore for the crustal stress measurement and monitoring borehole in Pinggu.By the contractive analysis，because of the intermediate principal stress，the minimum fluid column pressure required to maintain wellbore stable could be reduced.The minimum fluid column pressure derived from three criteria show the consistent variation trend with the depth in corresponding diagraph，which indicates that three criteria have their own applicability:Mohr-Coulomb criterion is conservative，Drucker-Prager criteria is somewhat dangerous and Mogi-Coulomb criterion is superior to the first two.

intermediate principal stress;strength criterion;the minimum fluid column pressure

P634.8

A

1672－7428(2012)04－0011－05

2011－09－29;

2012－02－14

梁涛(1985－)，男(汉族)，吉林人，中国地质大学(北京)硕士研究生，钻井工程专业，研究方向为地应力与井壁稳定性，北京市海淀区学院路29号，liangtao39@163.com。