软土三轴剪切蠕变试验研究及模型分析

杨 超，汪 稔，孟庆山

（中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071）

1 引 言

在自重或坡顶荷载作用下可能会发生基坑边坡滑移，导致新开挖基坑工程附近的建筑开裂或倾斜，严重危害基坑周围建筑物的安全。上海是典型的滨海相沉积软土地区，21世纪以来上海地区的基坑工程呈现出一些新的特点：基坑规模越来越大；开挖深度越来越深；场地临近建筑红线范围，周围含有大量管线等其他构筑物。工程实践表明，上海地区的基坑和建筑物地基等在长期荷载作用下变形具有明显的时间效应，即流变现象，这种现象严重危害基坑及基坑周围建筑物和构筑物的安全使用，因此，研究上海软土的剪切流变特性对上海地区工程建设有重要的现实意义。

软土剪切流变试验常采用三轴流变仪进行，由于测量技术上的限制，人们难以得到试样径向变形的准确值，直接影响对土的剪切流变特性的认识。通常径向变形通过试样的体积变化换算获得,试样径向变形的不均匀使测量结果存在一定误差，影响剪切应变的计算结果，且在不排水或非饱和三轴试验中更加难以获得试样的径向变形，无法获得试样的剪切应变。研究人员已经对传统三轴仪的径向量测方法进行了很多改进[1]，但这些测量方法受到操作难度或者测量精度的影响，多为接触式测量，会对试样产生约束，影响试验结果。

数字图像测量技术能够有效地弥补这些测量方法中的不足，在不接触试样的基础上实现试样变形的精确测量。这种方法是通过对图像的采集、处理分析和识别等一系列过程，量测图像中试样大小，实现对试样变形的测量。数字图像测量技术在土工三轴试验试样径向变形量测中已经取得了很好的效果[1－5]，实现了对三轴试样径向变形的直接测量，具有较高的测量精度。

2 数字图像测测量方法及误差分析

三轴蠕变试验的测量精度直接关系到试验结果的可靠性和准确性，因此，试验过程中应采取一定措施消除或减少测量系统带来的系统误差。

2.1 数字图像测量原理

数字图像通常表示为M×N个像素，在 Matlab中存储为一个多维数据矩阵。三轴试验数字图像测量时采用 unit8型数组的灰度图像来描述，像素灰度值用 0～255表示黑～白之间灰度变化[6]。在灰度图像下，物体边界表现为灰度值的不连续性，通过灰度函数的一阶或二阶导数变化即可判断出物体的边界位置。在实际图像处理过程中，常采用直方图或空域滤波器等手段增强图像的对比效果，以便在图像处理时准确判别试样边界。

2.2 三轴蠕变试验数字图像测量方法

利用数字图像测量方法进行三轴蠕变试验的试验装置主要由三轴蠕变试验系统、图像采集系统和数字图像处理系统三部分组成。三轴蠕变系统为应力控制式三轴仪，采用分级加载的方式进行；用数码相机进行三轴试样变形的图像采集，选择合适的位置固定相机三角支架，保证在整个试验过程中相机的位置不变，在试验开始之前进行相机对焦，整个试验过程中保持焦距不变，且镜头不发生偏移；按照试验的设计时长进行图像采集，并传入计算机，再应用 Matlab强大的数字图像处理功能对图像进行数字化处理分析，得到三轴蠕变试验中试样的变形信息。

2.3 系统标定

数字图像中每个像素点都表示一定的真实长度，通过对像素点的统计分析就可以准确获得物体的长度值，从而得到物体变形的真实值。

对测量系统标定可以获得每个像素代表长度的真实值。在距离物体 D处安放好图像采集仪后，计算长度为L0的物体所占的像素值N0，即可以得出每个像素在距离采集仪 D处代表的实际长度l：

测量时，可根据物体在图像中所占像素值N换算得到该物体实际的长度：L=lN。在标定和测量过程中保持采集仪和物体之间的距离D不变。

数字图像测量中，单位像素代表的真实长度越小，测量中产生的误差就越小，即l越小，测量精度越高。当测量精度要求很高时应优先选用像素较高的图像采集系统以保证试验结果的可靠性。

2.4 成像原理及误差分析

进行数字图像测量试样径向变形，实际测得的是弦AB的长度而不是直径2R的长度，因此，需要通过换算才能得到试样直径的长度2R。

由成像原理可知，成像时试验不同阶段中试样的弦AB、A′B′，镜头距试样中心的距离为D，其中 A、B、A′、B′分别为变形前和变形后图像物体的边缘（见图1），由三角函数关系有

由式（2）可以看出，当∠AOM 越接近π/2时，即试样半径R与镜头距试样中心的距离D比值R/D越小，弦AB与直径2R越接近。三轴试验试样直径常采用39.1 mm，当镜头距离试样中心1.0、1.5、2 m时，误差分别为0.0064、0.0032、0.0018 mm，相对误差仅为0.19%、0.08%、0.05%，此时测量误差与真值相比已达10-3量级，误差相对试样真实直径而言是一个非常小的值。因此，当镜头距离试样足够远时，可以用弦长AB近似代替试样直径2R。同样，当距离D一定时，半径R越小，弦长AB越接近直径2R长度，误差也越小。

图1 物体成像示意图Fig.1 Sketch of imaging

系统标定时，若采用较小直径圆柱进行标定，误差会随着试验中试样直径的增大而增大。因此，采用直径较大的圆柱径向进行标定，能够有效地降低在试验中试样鼓胀而产生的误差，保证试验质量。

3 三轴蠕变试验的数字图像测量成果

本次试验试样采用上海五号沟地区15 m深度处灰褐色淤泥质黏土进行三轴剪切蠕变试验，土的物理力学性质见表 1。上海五号沟地区临近长江口，与上海长江隧道工程相邻。长江口位于长江三角洲冲积平原的东南前缘，成陆较晚。60 m深度以上主要为饱和的黏性土和粉性土，具有含水率高、抗剪强度低、渗透性小、固结时间长、流变特性显著等特点。

试验采用分级加载方法，考虑所取土层深度的实际情况，选用围压σ3= 100 kPa进行三轴不排水和排水剪切蠕变试验和围压σ3= 200 kPa进行三轴排水剪切蠕变试验。试验共分5级进行加载，加载等级按照试样在相同条件下的三轴试验强度στ的1/5进行加载。

表1 土的物理力学性质参数Table1 Physico-mechanical properties of soil

3.1 三轴蠕变试验成果

图2～4为三轴剪切蠕变试验成果曲线（图中CU为三轴排水剪切试验，CD为三轴不排水剪切试验）。总体上看，较低偏应力水平D（偏应力水平指试样上施加的偏应力σ与破坏时最大偏应力στ之比，即D=σ/στ，D=0～1）下，试样变形稳定较快，表现为衰减蠕变。随着应力水平D的提高，逐渐表现为先稳定蠕变一段时间后发生衰减。当试样受到的D较高时，试样蠕变并未表现出明显的衰减现象，在很长时间内变形仍处于增长状态，此次加载历时14 d，试样变形还在缓慢增长。当试样偏应力σ达到三轴剪切试验强度στ时，试样在较短时间内产生大量变形，随后形成剪切面，剪切变形迅速增加发生剪切破坏。

不排水时，试验在前3级偏应力作用下，变形较小，土的结构较完整，偏应力主要由土体结构承受。当偏应力到达第四级时，土体结构已经被破坏，试样在加载后较短时间内产生大量变形且后期蠕变量也较大（见图2）。在排水条件下，剪切蠕变试验有明显的固结硬化现象，由于排水作用的影响，试样发生固结硬化强度提高，各级偏应力水平下产生的变形差异不如不排水条件显著（见图3）。

加载时，孔隙水压力在短时间内完成上升和下降过程（如图 2(b)～4(b)孔隙水压力与时间关系曲线）。不排水条件下，试样在受到竖向压力作用时，试样孔隙被压缩，由于无法排水，试样无法固结，孔隙水压力只能在试样内部孔隙之间实现平衡。加载过程中，孔隙水压力并无下降的趋势，经过短时间的平衡后，随着试样变形和孔隙的压缩，孔隙水压力呈缓慢上升趋势。由Terzaghi和Biot固结原理可知，排水时，加载瞬间孔隙水压力急剧上升，试样中的水在高压力下迅速排出产生固结。由于试样仅从试样顶部的透水石处排水，试样顶部土体很快发生固结，于是产生 Manadei-Cryer效应，孔隙水压力在一段时间内依然处于上升阶段，持续时间约为10 min。同时，在进行三轴排水剪切蠕变试验时排水路径受到限制，试样上部率先发生固结硬化，下部固结较慢，导致试样上部鼓胀通常较下端小，剪切面常常在试样下部形成。

土粒周围水膜的厚度决定着土体黏滞系数的大小，对软土流变起着十分重要的作用[7]。不排水试验中，土粒周围的水膜未发生明显的变化，试样的黏滞系数基本为一个定值，蠕变主要是由于土颗粒和土骨架的移动或变形产生的。排水时，受到竖向压力作用时，孔隙被压缩，试样中水被排出，土颗粒相互靠近，使得土粒之间水膜变薄，主要表现为土的密度增大，黏滞性增强，变形速率变小。随着试样中水进一步排出，土颗粒之间水膜越来越薄，土的黏滞性也越来越强。在试样加载初期，孔隙水压力迅速增大使得试样中水排挤较快，试样中土粒水膜厚度发生较大变化，土的固结和黏滞性变化明显。随着时间的推移，试样中排水速度逐渐减小，此时，土颗粒间的水膜厚度变化较小，相对稳定，试样中的黏滞系数变化缓慢。对照蠕变试验成果图可以看出，试验加载初期试样中厚度孔隙水压力和排水量较大，水膜变化也较大，与之对应的试样变形也较大为稳定蠕变；随后试样的孔隙水压力和排水量逐渐稳定，此时土颗粒间水膜厚度也变化不大，使得试样的黏滞系数基本为一个稳定的数值，试样变形逐渐稳定，即衰减蠕变，可见不排水条件下，随着加载等级的提高，试样的蠕变曲线的斜率较排水条件下大。

排水时，试样蠕变和固结相互影响。一方面，固结作用会使得土体发生硬化，从而减小试样的变形。另一方面，试样蠕变也会阻塞排水通道，影响土体的渗透性。试验中，固结和蠕变二者同时进行，并在一段时间内达到稳定平衡，整个过程中试样孔压消散与试样固结变形时间基本一致。

对比不同围压下排水时的蠕变曲线（见图3、4）可以发现，偏应力σ近乎相等时，围压为 100 kPa时试样变形量较围压为200 kPa时大，表明周围压力对土样的蠕变有较大的影响，但在相同偏应力水平 D下围压为 200 kPa时试样的变形量较围压为100 kPa时大。

3.2 图像测量法与排水体积法的比较

图5为采用图像测量方法和排水体积法测量得到的剪切蠕变曲线。剪切应变-时间对数曲线与垂直应变-时间曲线变化相似，是由于试样的剪切应变是通过轴向应变和径向应变计算得到，而径向的变形相对轴向小很多，但通过两种不同测量方法获得的剪切应变有一定的差别。在偏应力水平较低时，图像测量方法与排水体积方法得到的剪切应变值相差不大，曲线基本重合；随着偏应力水平D增大，二者差值逐步增大，图像测量得到的剪切应变值大于排水体积方法得到的剪切应变值。这一现象符合实际情况，在三轴试验过程中，试样变形是不均匀的，此次图像测量方法得到的是试样1/2高度截面的变形值，而排水体积方法得到的是整个试样的平均变形。在偏应力水平较低时，试样径向变形较小，试样1/2高度截面处的变形值与整个试样的平均变形相差不大；随着偏应力水平的增大，试样发生鼓胀变形，试样1/2高度截面的变形值明显比试样整体变形的平均值大，随着变形发展这个差值逐渐增大（见图 6）。采用试样排水体积的方法进行测量获得的剪切应变值也随试样变形的发展误差在不断扩大。

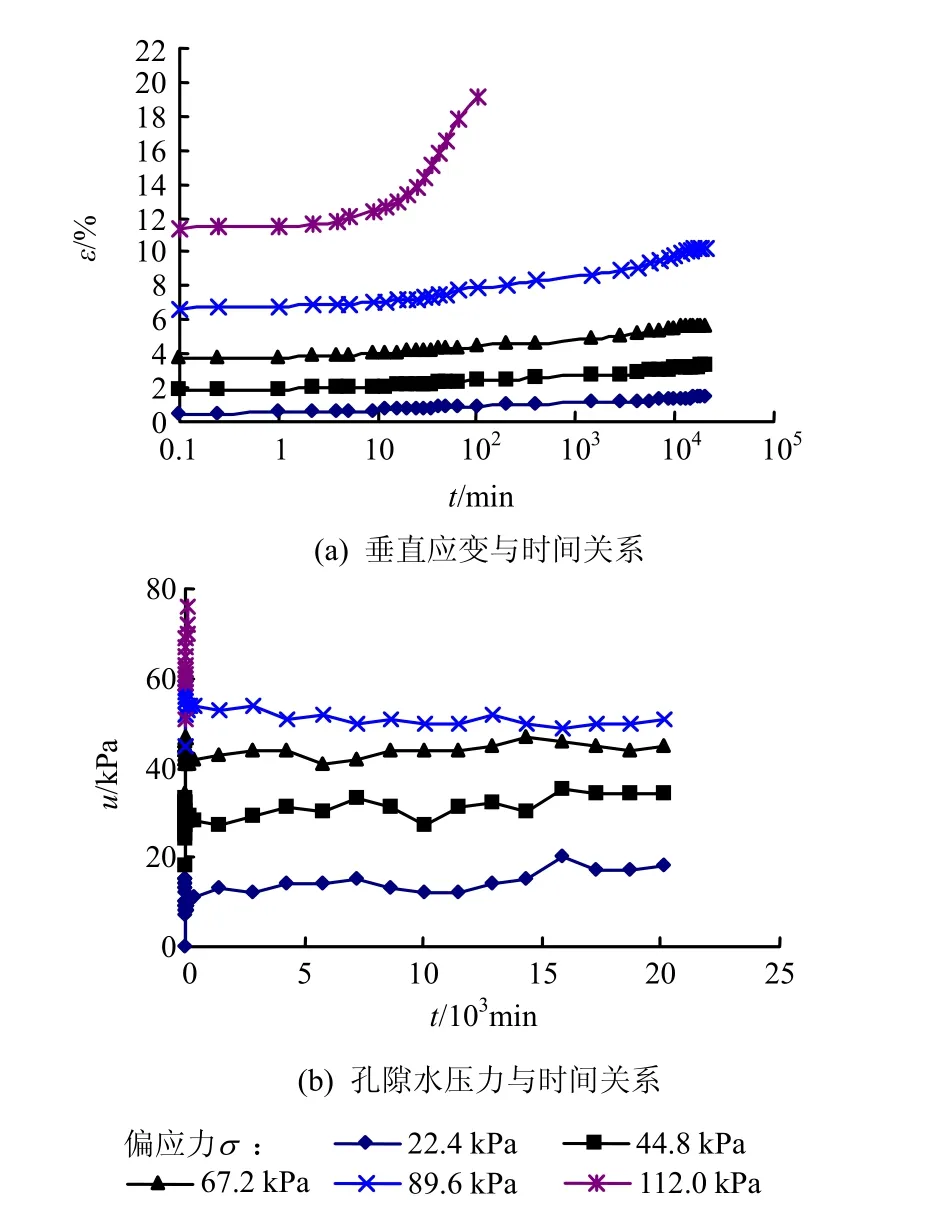
图2 σ3＝100 kPa时CU三轴蠕变试验成果Fig.2 Results of CU triaxial creep test (σ3＝100 kPa)

图3 σ3＝100 kPa时CD三轴蠕变试验成果Fig.3 Results of CD triaxial creep test (σ3＝100 kPa)

图4 σ3＝200 kPa时CD三轴蠕变试验成果Fig.4 Results of CD triaxial creep test (σ3＝200 kPa)

图5 不同测量方法的剪切应变与时间关系曲线Fig.5 Relationships of shear strain and time in different measuring methods

图6 不同偏应力下试样的二值图Fig.6 Binary images in different deviatoric stresses

3.3 图像测量与排水体积法得到的Singh-Mitchell模型参数比较

Singh-Mitchell提出能够恰当描述多种土在20%～80%范围内偏应力水平的应变速率-时间关系特征方程[8－10]：

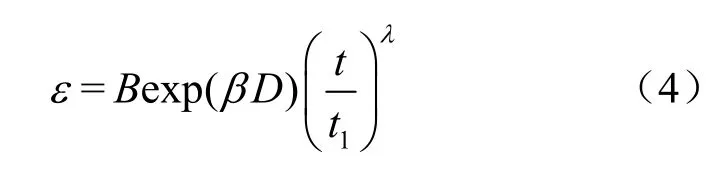
图7为 3种不同情况下三轴剪切蠕变试验的lnε-lnt关系曲线和lnε-D关系曲线。由图可以看出，不排水条件下各级偏应力作用下剪切应变和时间在双对数坐标下线性关系良好，且斜率基本一致。排水条件下，除第一级偏应力下直线斜率差别较大以为外，其他各级偏应力水平下lnε-lnt曲线基本平行，且图像测量方法和排水体积方法获得的lnε-lnt曲线基本重合。图中选用t1=1 d时lnε-D曲线进行 Singh-Mitchell模型参数的确定，由图可以看出，lnε和D之间线性关系明显，线性相关系数分别为0.9867、0.9740和0.9947。因此，采用具有广泛应用的 Singh-Mitchell模型是适合的，其中λ为lnε-lnt的斜率。各参数见表3。

通过两种不同的测量方法获得的 Singh-Mitchell模型参数的差别不大（见表2），应力水平较低且难以准确测量径向变形时可近似用排水体积法进行参数确定。同时，Singh-Mitchell模型很好的描述上海软土在偏应力水平在20%～80%范围内的流变特性，对于工程应用基本可以满足要求。排水时，对于偏应力水平大于80%时上海软土剪切流变特性也可以较好的描述，而对于偏应力水平低于20%时软土的剪切流变特性的描述差别较大。

图7 不同条件下lnε-lnt曲线和lnε-D曲线Fig.7 Curves of lnε-lnt and lnε-D in different test conditions

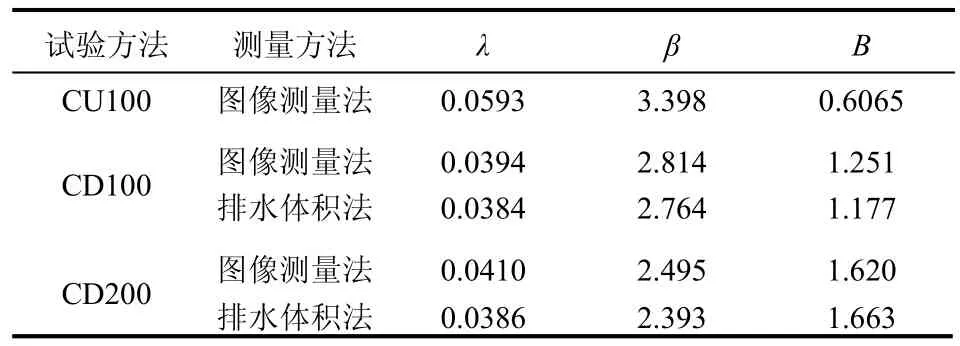
表2 Singh-Mitchell模型参数Table2 Parameters of Singh-Mitchell model

4 结 论

（1）数字图像测量技术简单实用，且测量精度较高，能够满足高精度土工试验测量的需要。在三轴蠕变试验中能够有效的测得试样的径向变形，实现试样的非接触式测量，减少接触式测量对试验结果的影响，为难以测量试样体积变化的不排水试验和非饱和试验提供了有效的径向变形测量途径。

（2）进行三轴蠕变试验图像测量时，必须严格保证图像采集系统的镜头在标定和试验过程中不发生偏移或不产生相对位置变化，避免由于镜头偏移而产生测量误差；试样鼓胀会使测量误差增大，采用较大直径的圆柱进行图像测量标定能够有效的抑制这一现象的产生，提高测量精度。

（3）在三轴排水剪切蠕变试验中，在短时间内孔隙水压力会持续上升产生 Manadei-Cryer效应，整个过程历时约10 min。试验过程中，排水路径的影响使得试样上部率先发生固结硬化，试样鼓胀和剪切面通常偏向试样下部产生。

（4）软土的流变性质与土中水的含量密切相关。土中含水率高时，土颗粒周围水膜较厚，黏滞系数较低，土颗粒移动相对较容易；反之，水膜较薄，黏滞系数较大。排水剪切流变试验时，随着随着土体中水的排出土样中水含量减少，颗粒周围的水膜变薄，土的密度增大、黏滞性增强，土的流变性减弱。

（5）由于试样变形的不均匀，获得土的剪应变时图像测量方法和排水体积测量方法存在一定的差异。图像测量方法在获得土的剪应变时排水体积法要大，随着荷载等级的增加、试样鼓胀变形增大，这一差别更加明显。在进行 Singh-Mitchell模型参数确定时，两种方法获得的参数差别不大，在径向变形不大且难以准确测量时可用排水体积法代替。

本次试验仅从一个方向进行试样变形的图像采集，当试样产生上不均匀变化或形成剪切面时不能准确获取试样滑移的试验信息，建议在试验时至少从两个方向获得试验变形图像以便准确合理的获取试样变形信息。

[1]邵龙潭,王助贫,韩国城,等. 三轴试验土样径向变形的计算机图像测量[J]. 岩土工程学报,2001,23(3): 337－341.SHAO Long-tan,WANG Zhu-pin,HAN Guo-cheng,et al.Digital image processing technique for measurement of the radial deformation of specimen in triaxial test[J].Chinese Journal of Geotechnical Engineering,2001,23(3): 337－341.

[2]Ali Hakan Ören,Okan Önal,Gürkan Özden,Abidin Kaya.Nondestructive evaluation of volumetric shrinkage of compacted mixtures using digital image analysis[J].Engineering Geology,2006,85: 239－250.

[3]刘永禄. 三轴实验土样变形数字图像测量的实现[D].大连: 大连理工大学,2002.

[4]邵龙潭,孙益振,王助贫,等. 数字图像测量技术在土工三轴试验中的应用研究[J]. 岩土力学,2006,27(1):29－34.SHAO Long-tan,SUN Yi-zhen,WANG Zhu-pin,et al.Application of digital image processing technique to triaxial test in soil mechanics[J]. Roch and Soil Mechanics,2006,27(1): 29－34.

[5]董建军,邵龙潭,刘永禄,等. 基于图像测量方法的非饱和压实土三轴试样变形测量[J]. 岩土力学,2008,29(6): 1618－1622.DONG Jian-jun,SHAO Long-tan,LIU Yong-lu,et al.Measurement of deformation of unsaturated compacted soil triaxial specimen based on digital image measurement method[J]. Rock and Soil Mechanics,2008,29(6): 1618－1622.

[6](美)冈萨雷斯(Gonzalez),等. 数字图像处理(MATLAB版)[M]. 阮秋琦,等译. 北京: 电子工业出版社,2005.

[7]何俊,肖树芳. 结合水对海积软土流变性质的影响[J].吉林大学学报,2003,33(2): 204－207.HE Jun,XIAO Shu-fang. Some influence of bond water on rheological properties of marine soft soils[J]. Journal of Changchun University of Science and Technology,2003,33(2): 204－207.

[8]SINGH A,MITCHELL J K. General stress-strain-time function for soils[J]. Journal of Soil Mechanics and Foundation Division,ASCE,1968,94(1): 21－46.

[9]李军世,林咏梅. 上海淤泥质粉质黏土的 Singh-Mitchell蠕变模型[J]. 岩土力学,2000,21(4): 363－366.LI Jun-shi,LIN Yong-mei. Singh-Mitchell creep model of Shanghai very soft silty clay[J]. Rock and Soil Mechanics,2000,21(4): 363－366.

[10]王常明,王清,张淑华. 滨海软土蠕变特性及蠕变模型[J]. 岩石力学与工程学报,2004,23(2): 227－230.WANG Chang-ming,WANG Qing,ZHANG Shu-hua.Creep characteristics and creep model of marine soft soils[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(2): 227－230.