改进压缩感知的舰船数字图像水印算法

徐 沛，沙长涛

(中国电子技术标准化研究院，北京 100176)

0 引言

在舰船目标识别与路径规划等领域中，需远程传输舰船数字图像。为提升舰船数字图像传输的安全性，确保舰船安全航行，需对舰船数字图像进行水印处理，防止遇到攻击时，出现信息泄露问题[1–3]，影响舰船航行安全。

为此需研究图像水印算法，提升图像安全性，确保舰船安全航行。沈艳冰等[4]将舰船RGB 图像变更成YCrCb 图像，并提取Y分量，得到对角矩阵，通过加性规则将水印嵌入对角矩阵内，完成水印嵌入，该算法在承受噪声攻击时，可有效嵌入水印，具备较优的水印嵌入效果。李淑芝等[5]先分块处理原始图像，通过各分块的灰度共生矩阵，得到图像的纹理特征，并求解纹理特征的复杂度，再降序排列纹理特征，用于确定水印嵌入位置，依据嵌入位置求解各分块的JND值，通过JND 值设计水印嵌入规则，完成图像水印嵌入，该算法具备水印嵌入的可行性。但这2 种方法均不具备抗旋转与抗剪切攻击能力，当图像存在旋转与剪切情况，这2 种算法的水印嵌入效果均较差。

改进压缩感知理论可利用较少的信息，完成原始图像的重构，大幅度减轻信息传输的压力[6]，具备较优的稳定性与抗剪切攻击能力等，正交匹配追踪为常见的压缩感知重构算法。为此研究改进压缩感知的舰船数字图像水印算法，提升水印嵌入与提取效果。

1 舰船数字图像水印算法

利用改进压缩感知理论，对舰船数字图像进行水印处理，提升舰船数字图像的安全性，具体原理为：先通过离散小波变换（discrete wacelet transform，DWT）稀疏分解舰船数字载体图像，获取舰船数字载体图像的高频与低频系数矩阵；再通过改进压缩感知理论获取测量观测矩阵，依据观测矩阵处理高频与低频系数矩阵，获取相应的舰船数字图像系数矩阵观测值；然后在高频系数矩阵观测值内嵌入水印，并存储嵌入位置的分块索引，构建索引矩阵。最后通过改进压缩感知理论内的改进正交匹配追踪算法，重构高频与低频舰船数字图像系数矩阵的观测值，获取高频与低频系数矩阵，并融合这2 个矩阵，同时对其展开离散小波反变换处理，获取嵌入水印的舰船数字图像。

1.1 基于DWT 的舰船数字图像稀疏分解

利用改进压缩感知理论水印处理舰船数字图像水印时，舰船数字图像信号越稀疏，重构效果越佳[7]，因为原始舰船数字图像矩阵不是稀疏矩阵，所以需要通过DWT 稀疏分解原始图像。

利用DWT 稀疏分解原始舰船数字图像信号后，可获取图像各子频段的信号，且获取的信息非常丰富[8]，为舰船数字图像重构提供丰富的信息，提升舰船数字图像重构质量。令舰船数字图像系数处理时，离散小波是ψ(t)，公式如下：

其中：t为时间；a为伸缩因子；b为平移因子；m为尺度因子；n为舰船数字图像信号长度。

舰船数字图像的DWT 如下：

其中：f(t)为离散函数；R为实数集。

利用高通滤波器处理的舰船数字图像X，获取舰船数字图像的高频系数矩阵，公式如下：

其中：z为舰船数字图像信号高频系数矩阵尺度；h(m)为高通滤波器。

通过扩展尺度因子，扩展倍数为2 倍，可提升DWT的可逆性，扩展后的舰船数字图像信号高频系数矩阵为：

利用低通滤波器处理X′，获取舰船数字图像的低频系数矩阵，公式如下：

其中，g(m)为低通滤波器。

1.2 基于改进压缩感知的舰船数字图像水印算法的实现

利用压缩感知理论获取获取舰船数字图像高频与低频系数矩阵的观测值，以获取低频系数矩阵的观测值为例，令舰船数字图像高频系数矩阵的信号长度为l，时域元素为，如果舰船数字图像低频系数矩阵内的元素，可在某组正交基φ={φ1,φ1,···,φl}下稀疏分解，同时为K-稀疏的，则在 φ中的线性投影为：

其中：θ为变换域下的系数矢量，同时 θ是K-稀疏的；φ为维数L×L的变换矩阵。

令舰船数字图像高频系数矩阵的观测矩阵是Φ1，那么观测获取舰船数字图像高频系数矩阵的观测值为：

其中：Q1=Φ1φ为高频系数矩阵的压缩感知矩阵。

利用Kent 混沌序列替换 Φ1，因为Kent 混沌序列具备较优的稳定性，所以以Kent 混沌序列为测量矩阵，可提升后期舰船数字图像观测值重构的精度。

Kent 混沌映射为离散混沌系统，且具备代表性，表达公式如下：

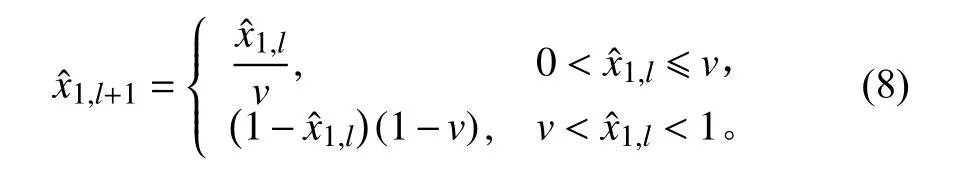
其中：v∈(0,1)为控制参数；为舰船数字图像高频系数矩阵内元素序列。

其中：σ为序列方差；λ为标准化系数。

在舰船数字图像高频系数矩阵的观测值内嵌入水印后，利用改进压缩感知理论内的改进正交匹配追踪算法，重构舰船数字图像高频与低频系数矩阵的观测值。具体步骤如下：

步骤1输入压缩感知矩阵Q，舰船数字图像系数矩阵观测值s，的稀疏度K，残差上限ε。

步骤2计算残差d和内每一列的内积ui=|〈d,Qi〉|，获取最大内积值

步骤3如果某原子符合，那么将该原子添加至索引集 ξ内，完成原子筛选。其中，η为门限因子。

步骤4更新 ξ与原子集Hξ。数矩阵观测值的估计值。其中，

步骤5通过最小二乘法求解原始舰船数字图像系α为修正系数。

舰船数字图像高频与低频系数矩阵观测值均由上述步骤进行重构，重构后的高频与低频舰船数字图像系数矩阵是。

在舰船数字图像系数矩阵观测值嵌入水印的具体步骤如下：

步骤1分块处理原始舰船数字载体图像X，X的尺寸是n×n，分块大小是β×β，利用DWT 稀疏分解X，获取舰船数字图像高频与低频系数矩阵。

步骤2通过尺寸是β×β的舰船数字图像分块，对展开分块压缩感知，获取舰船数字图像高频与低频系数矩阵观测值s1与s2。

步骤3Arnold 置乱处理待嵌入的舰船数字图像水印O，获取置乱水印，增强水印的抗剪切攻击性能，公式如下：

其中：水印置乱前后的像素是(p,q)，(p′,q′) ；ρ为水印的阶。

其中：ς为比例因子；α为修正系数。

嵌入时，令各分块舰船数字图像系数矩阵观测值最多能够嵌入一次，提升水印的透明性。为提升水印鲁棒性，将反复嵌入4 次，并存储每个已嵌入的位置信息，即分块索引号，通过分块索引号，建立索引矩阵 Θ，以 Θ 与为提取的密钥，提高水印安全性。

步骤5嵌入完成后，通过改进正交匹配追踪算法重构s1与s2，获取，将融合成稀疏的舰船数字图像系数矩阵，对展开离散小波反变换获取嵌入后的舰船数字图像。

2 实验分析

以大小为512×512 的舰船数字图像为实验载体图像，以大小为50×50 的二值化图像为水印，利用本文算法将水印嵌入舰船数字图像内，分析本文算法的水印嵌入与提取效果。

实验舰船数字图像与水印图像如图1 所示。

图1 舰船数字图像与水印图像Fig.1 Ship Digital Image and Watermark Image

利用本文算法在实验舰船数字图像内嵌入水印，嵌入水印后的舰船数字图像如图2 所示。

图2 嵌入水印后的舰船数字图像Fig.2 Digital image of ship embedded with watermark

由图2 可知，本文算法可有效在实验舰船数字图像内嵌入水印，与原始图像对比可知，嵌入水印后的图像与原始图像基本无差别，说明本文算法具备较优的水印嵌入透明性。

在嵌入水印后的舰船数字图像内加入椒盐噪声，利用本文算法在加入噪声后的舰船数字图像内，提取水印，提取结果如图3 所示。

图3 水印提取结果Fig.3 Watermark extraction results

由图3 可知，本文算法可有效在加入椒盐噪声后的实验舰船数字图像内，提取水印，与原始水印对比可知，提取的水印内虽然包含大量噪声，但依旧能够提取完整的水印。实验证明：在舰船数字图像内加入椒盐噪声后，本文算法具备水印提取的有效性。

利用峰值信噪比（PSNR）衡量水印嵌入的透明性，利用归一化相关系数（NC）衡量水印提取精度，PSNR 与NC 值越高，说明水印嵌入与提取的透明性越佳、精度越高，PSNR 以及NC 分别对应的阈值是30 dB 与0.7。分析本文算法在不同图像压缩质量因子时，对实验舰船 水数字图像嵌入与提取效果，分析结果如图4 所示，压缩质量因子大小与压缩后舰船数字图像内有效信息量呈正比。

由图4 可知，随着图像压缩质量因子的提升，本文算法提取舰船数字图像水印时的NC 值呈上升趋势，当图像压缩质量因子达到40%时，NC 值上升至最高值，并趋于稳定，稳定在0.98 左右，最低NC 值在0.73 左右，并未低于设置阈值，说明在不同图像压缩情况下，本文算法提取的水印与原始水印均非常接近，即水印提取精度较高；图像压缩质量因子与PSNR 值具有正相关关系，当图像压缩质量因子达到35%时，PSNR 值达到最大值，并趋于稳定，稳定在48 dB 左右，最低PSNR 值在31 dB 左右，并未低于设置阈值，说明在不同图像压缩情况下，本文算法嵌入水印的透明性均较优。

图4 舰船数字图像水印嵌入与提取效果Fig.4 Watermark embedding and extraction effect of ship digital image

3 结语

在传输舰船数字图像时，需对其进行水印处理，提升舰船数字图像的安全性。为此，本文研究改进压缩感知的舰船数字图像水印算法，提升水印嵌入的透明性与水印提取精度，应用水印算法后，可有效提升图像的安全性，为促进舰船数字图像水印领域的发展提供参考依据。