反正切函数联合参数的凸组合最小均方滤波算法
2012-11-04谢子殿董志国崔师明
谢子殿, 董志国, 崔师明
(黑龙江科技学院 电气与信息工程学院, 哈尔滨 150027)
反正切函数联合参数的凸组合最小均方滤波算法
谢子殿,董志国,崔师明
(黑龙江科技学院 电气与信息工程学院, 哈尔滨 150027)
为解决传统最小均方自适应滤波算法联合参数λ(n)运算量大、收敛速度慢的问题,提出一种基于修正的反正切函数的凸组合最小均方滤波算法,并应用Matlab软件对不同信噪比算法进行仿真比较。结果表明:该算法在保证运算量的前提下,能够加快算法的收敛速度及减小其稳态误差。反正切函数联合参数的凸组合最小均方滤波算法具有更好的滤波性能。
凸组合; 自适应滤波; 反正切函数
0 引 言
自适应滤波技术可应用于通信领域的自动均衡、回波消除、天线阵波束形成,以及其他有关信号处理的参数识别、噪声消除、谱估计等方面。自20世纪40年代N.维纳采用最小均方LMS准则设计最佳线性滤波器以来,各种基于LMS的改进算法层出不穷[1-3]。
凸组合自适应滤波算法具有并行运算、较快的收敛速度和较小的稳态误差的特点。它的基本原理是:利用两个步长分别为μ1和μ2的自适应滤波器并行独立处理数据。其中,μ1为小步长滤波器步长,μ2为大步长滤波器步长,联合参数λ(n)调节μ1和μ2的比例。传统的凸组合滤波算法CLMS的联合参数λ(n)是Sigmoid的函数,文献[4]提出了一种基于萁舌线函数的CLMS算法。这两种算法收敛速度慢、λ(n)函数运算复杂。
笔者在文献[5]的基础上提出一种基于改进的反正切函数快速凸组合最小均方滤波算法ATLMS。与Sigmoid的函数和萁舌线函数不同,提出的改进反正切函数在迭代运算中期以前具有比较缓慢的变化,从而保证μ2在算法中起主要调节作用以加快收敛。在运算上,Sigmoid函数引入指数运算,萁舌线函数运算时需要判断迭代运算的正负,都有较大的运算量。
1 凸组合自适应滤波原理
凸组合自适应滤波是由两个权系数分别为ω1(n)和ω2(n)的LMS滤波器组成,由图1中虚线框所示。二者独立并行运行,互不干扰,各自输出值Y1(n)和Y2(n)在联合参数λ(n)的调解下重新组合得到系统的最终输出Y(n)。
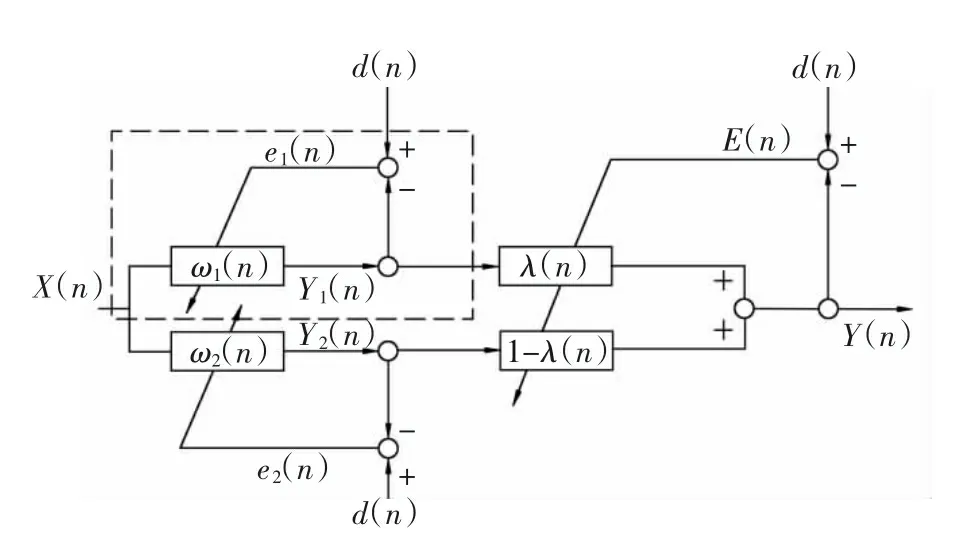
图1 凸组合自适应滤波原理
现假定ω1(n)为小步长滤波器权值,ω2(n)为大步长滤波器权值,输入为x(n),期望响应为d(n),u1、u2分别为两滤波器的步长因子,则:
ω1(n+1)=ω1(n)+u1×e1(n)x(n),
ω2(n+1)=ω2(n)+u2×e2(n)x(n)。
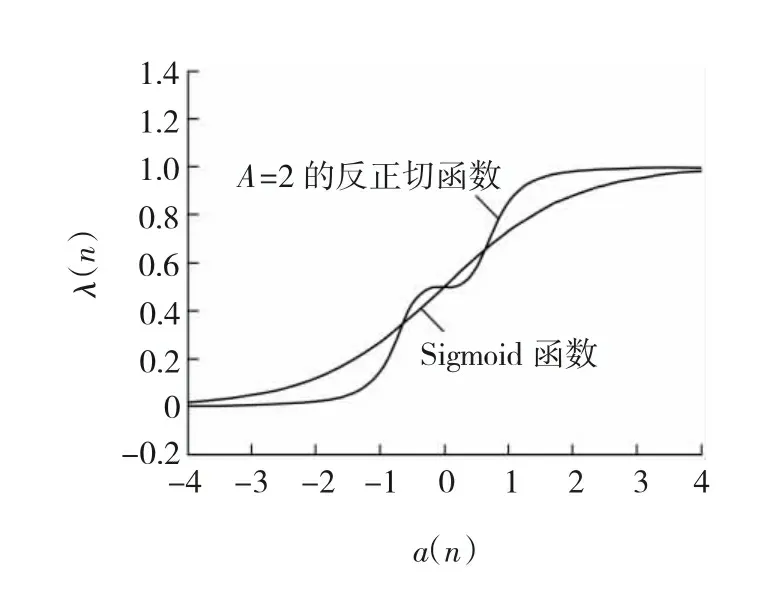
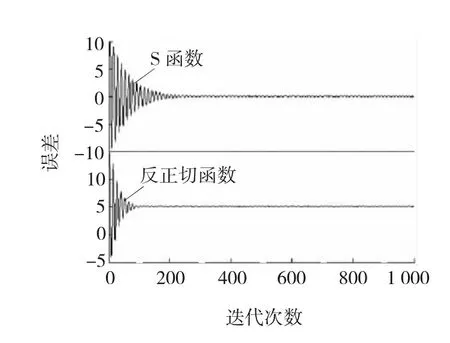
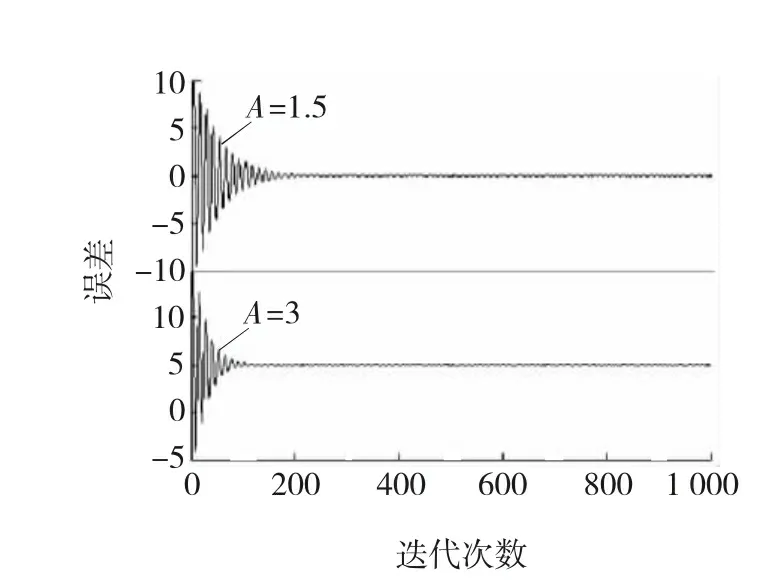
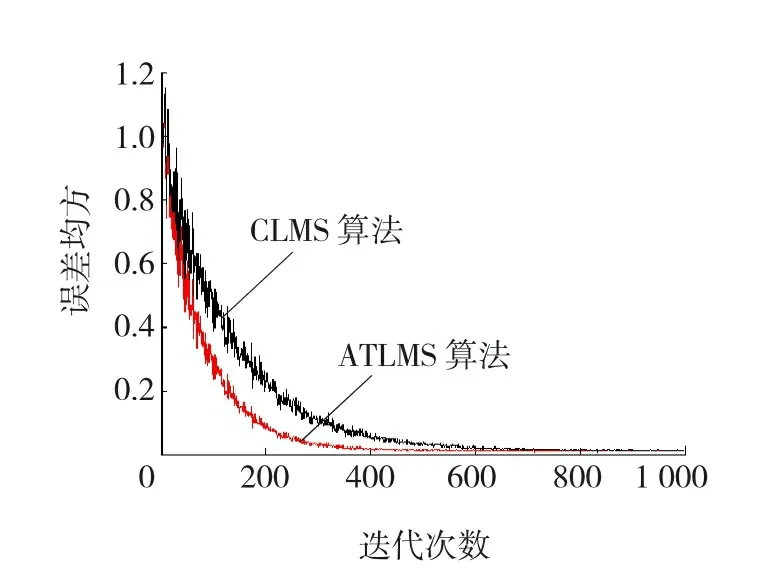
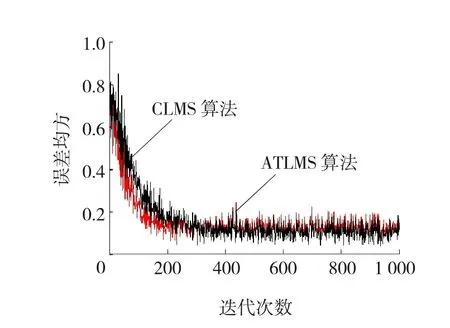
根据自适应滤波原理的稳定性,步长u需满足如下收敛条件:0 系统等效输出为 Y(n)=λ(n)×Y1(n)+(1-λ(n))×Y2(n)。 等效输出误差: E(n)=λ(n)e1(n)+[1-λ(n)]e2(n), 式中,λ(n)——基于S函数。 λ(n)=sgm [a(n)]=1/(1+e-a(n))。 (1) 输出误差: E(n)=d(n)-Y(n)。 参数a(n)的值决定了联合参数λ(n),进而直接决定输出Y(n)误差大小。通常采用最小均方法确定: a(n)-uaE(n)(e1(n)- e2(n))λ(n)(1-λ(n)), 式中,ua——a(n)的自适应步长。 在凸组合自适应滤波中,联合参数λ(n)决定着系统性能的优劣。Sigmoid函数具有更快速的趋近于上下边界的性能,这对于CLMS算法来说非常不利,因为经过大量的复杂运算后,得出的联合参数往往由于非常逼近0或1而导致凸组合函数失去实际的效能[5]。基于此考虑,常常需要限制a(n)的取值范围,要求a(n)∈[-4,+4]。 文献[4]提出了基于萁舌线函数的凸组合滤波器。萁舌线函数在收敛初始和结束时有比较平稳的变化,但是在a(n)=0附近和Sigmoid函数一样,依旧有比较快的下降/上升速度。这样的变化曲线导致的结果是:随着迭代运算进行,λ(n)的值几乎由0跳变到1。 为了解决S函数和萁舌线函数在迭代速度和运算量上的缺陷,笔者提出基于改进的反正切函数的联合参数表达式: (2) 为了改进函数形状以满足不同条件下的算法要求,可加入参数因子A,即式(2)改为 (3) 其函数图形如图2所示。 图2 Sigmoid函数与改进的反正切函数对比 Fig. 2Comparison diagram of Sigmoid and improved arc-tangent function 由图2可以看出,改进的反正切函数与Sigmoid函数相比较(萁舌线函数同Sigmoid函数类似,分析略),在迭代初期和末期保持较平稳的变化,使λ(n)的值保持在0或1,而在运算中期λ(n)保持在0.5左右。 现把基于改进的反正切函数的迭代运算过程分为三个部分:迭代运算开始被称为加速收敛期。此时λ(n)→0,由式(1)得,系统输出值Y(n)≈Y2(n),即大步长LMS趋于单独作用而小步长LMS被屏蔽,故加速收敛。运算中期被称为过渡期。这段时间里对运算的收敛速度和稳定性并无严格的要求,因而取λ(n)值约为0.5。同时为了适应不同的算法要求,可以修改参数因子A的大小以加快或减少过渡期如图3所示,体现了该算法的灵活性。例如,当环境要求算法要对均方差有更快的响应速度时,可增加A值使其过渡期更小,加速收敛期更大以加快收敛速度。同时,当外界噪声比较严重时,系统对算法的鲁棒性有更高的要求,减小A值使过渡期进而减慢收敛速度。迭代后期称为稳定期。λ(n)→1,系统输出值Y(n)≈Y2(n),小步长LMS趋于单独作用而大步长LMS近似被屏蔽,以减少算法的稳态误差。 图3 不同A值函数对比 Fig. 3Comparison diagram of arc-tangent function with different parameter values 比较S函数和文中所提出的函数,在收敛速度上,该算法具有明显的优势,尤其能够灵活的适应不同的环境要求;在运算量上,ATLMS算法不需要进行指数运算因而能够节约大量的运算;在收敛性能上二者基本相同,因此整体上该算法较传统的CLMS具有较大的优势。 3.1假设 对凸组合系统进行如下假设[7]: (1)期望信号d(n)与输入信号x(n)的线性衰减模型: 式中:ω0——未知的权向量; e0(n)——方差为σ2的独立噪声。 (2)两滤波器的初始权向量ω1(0)、ω2(0)与初始a(0)对任意的n值独立{x(n),d(n),e0(n)}。 (3)E[x(n)]=0,E[x(n)xT(n)]=R, E[d(n)]=0,E[e0(n)]=0。 (4)μ和e(n)、x(n)、Δω(n)相互独立。 3.2参数 单个滤波器和组合滤波器定义如下参数: 单个滤波器的权值向量误差: Δω(n)=ω(n)-ω0, 先验误差: ea(n)=ΔωT(n)x(n)。 3.3性能 滤波器的性能用额外均方误差EMSE来表示,其定义为滤波器在工作时除最小均方差以外的额外误差项。滤波器输出误差项: e(n)=ea(n)+e0(n), 有两个滤波器的EMSE表达式: 定义基于先验误差的交叉EMSE表达式: 根据上式和柯西不等式有如下结论: Jex,12(∞)≤max{Jex,1(∞),Jex,2(∞)},即交叉EMSE不会同时高于两个滤波器的EMSE。 以下证明,滤波器工作时,组合滤波器优于任何单个滤波器的性能。 组合滤波器的误差为 e(n)=λ(n)e1(n)+[1-λ(n)]e2(n)+e0(n)。 为了简化运算,不考虑噪声引入,得组合滤波器先验误差项: ea(n)=λ(n)ea,1(n)+[1-λ(n)]ea,2(n)。 则有组合滤波器的EMSE: λ2(n)Jex,1(∞)+[1-λ(n)]2Jex,2(∞)。 由于λ(n)∈(0,1),根据不等式定理有: Jex(∞) Jex(∞) 即组合滤波器优于单个滤波器的性能。 仿真系统为20阶FIR模型,取1 000个采样点分别进行200次运算取平均值。输入信号x(n)为幅值10的正弦波信号,系统噪声r(n)为与输入信号不相关的高斯白噪声,信噪比为30 dB。 4.1对比实验 基于S函数与反正切函数的凸组合自适应滤波算法作为对比实验,对式(3)取修改因子A=3,分别得到两种算法的误差曲线,如图4所示。 图4 S函数与反正切函数算法误差 Fig. 4Error of S function and arc tangent function algorithm 由图4可见,ATLMS算法比传统的CLMS算法在收敛速度上较快,而在稳态误差方面,二者几乎相近(图4中稳态时期的波纹是由于截图是在原图缩放情况下截取造成的)。 4.2参数A对算法的影响 在不同的环境下,可以通过调节过渡期的长短来满足算法要求。现取不同的A值研究其对算法的影响,分别取A=1.5、3作对比,如图5所示。 图5 不同A值对ATLMS算法影响 Fig. 5Effect of CLMS algorithm with different parameter values 如图5所示,当A较大时,过渡期较短,算法的收敛速度较快,这和文中原理分析是吻合的。 4.3信噪比对算法收敛性的影响 图6 SNR=20两种算法的学习曲线 Fig. 6Comparison of two CLMS algorithms under condition of SNR=20 由图6可见,在高信噪比下,反正切算法较CLMS算法有更快的收敛速度。由于两种算法采用同样的框架,因而在稳态性能上基本一致,反正切算法没有优势。 图7 SNR=2两种算法的学习曲线 Fig. 7Comparison of two CLMS algorithms under condition of SNR=2 由图7可见,在低信噪比条件下,两种算法的性能都急剧下降,稳态误差上升。在收敛速度方面,反正切算法有微弱的优势,但较之其他的自适应滤波算法,反正切算法还是具有较好的收敛性能。 改进的反正切函数的凸组合滤波算法ATLMS较传统自适应滤波算法LMS在收敛速度和算法复杂程度上都有显的优势,同时,在稳态误差方面保留了原算法的优点。调节改进的反正切联合参数λ(n)的过渡期大小,可以满足算法在不同的环境条件下的要求。 [1]李建平, 蒙建波. 基于双曲函数的变步长LMS算法及其分析[J]. 传感器与微系统, 2011, 30(5): 127-128. [2]袁江南, 汤碧玉, 陈辉煌. 基于信噪比的改进变步长LMS算法及应用[J]. 厦门大学学报: 自然科学版, 2011, 50(5): 829-833. [3]王新. 自适应滤波器的新型变步长算法及其应用[J]. 电机与控制学报, 2011, 15(4): 23-27. [4]于霞, 刘建昌, 李鸿儒. 基于箕舌线函数的快速凸组合最小均方算法[J]. 系统仿真学报, 2010, 22(5): 1097-1105. [5]ARENAS GARCIA J, FIGUEIRAS VIDAL A R, SAYED A H. Steady state performance of convex combinations of adaptive filters [J]. IEEE Signal Processing, 2005, 4(4): 33-36. [6]何振亚.自适应滤波处理[M]. 北京: 科学出版社, 2003: 22-38. [7]ARENAS GARCIA J, FIGUEIRAS VIDAL A R, SAYED A H. Mean-square performance of a convex combination of two adaptive filters[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 1078-1090. [8]庞彦军, 刘立民, 马丽涛, 等. 基于非线性序转换的层次分析模型[J]. 河北工程大学学报: 自然科学版, 2011, 28(2): 109-112. (编辑李德根) Convex combination of least mean square algorithm based on arc-tangent function XIEZidian,DONGZhiguo,CUIShiming (College of Electric & Information Engineering Heilongjiang Institute of Science & Technology, Harbin 150027, China) Aimed at a solution to complex computation and poor convergence performance of the convex parametric ofλ(n) in the least-mean-square(LMS) algorithm, this paper proposes a new CLMS algorithm based on improved arc-tangent function and introduces simulation comparison of algorithms with different SNR by using MATLAB math software. The simulation indicates that this new algorithm, able to quicken the convergence and reduce steady state error, along with assuring less computation, demonstrates a better filtering performance. convex combination; adaptive filter; arc-tangent function 1671-0118(2012)06-0608-05 2012-10-08 谢子殿(1962-),男,黑龙江省鹤岗人,教授,研究方向:计算机自动控制、嵌入式系统技术,E-mail:xiezd@163.com。 TN713 A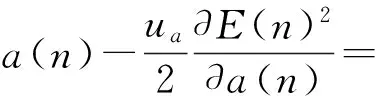
2 反正切函数的联合参数
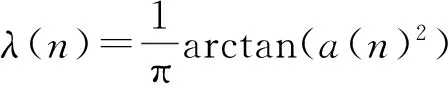


3 凸组合滤波性能分析
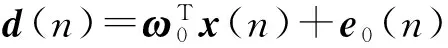
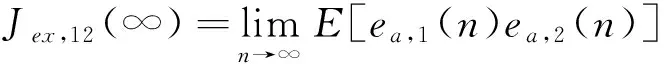
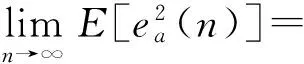
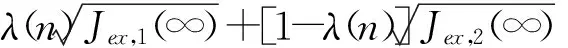
4 仿真分析
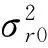
5 结束语
