Zakharov方程组全离散Fourier谱格式的稳定性

孙　璐,　张法勇,　陈洪海,　王　春

(1.黑龙江科技学院 理学院, 哈尔滨 150027;2.黑龙江大学 数学科学学院, 哈尔滨 150080)



Zakharov方程组全离散Fourier谱格式的稳定性

孙璐1,张法勇2,陈洪海1,王春1

(1.黑龙江科技学院 理学院, 哈尔滨 150027;2.黑龙江大学 数学科学学院, 哈尔滨 150080)

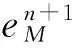
Zakharov方程组; Fourier谱格式; 全离散; 稳定性

0　引　言

在等离子物理学中出现如下方程组的周期初边值问题:

iEt+Exx=NE,

(1)

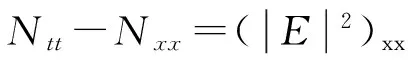
(2)

E(x,0)=E0(x),

(3)

N(x,0)=N0(x),Nt(x,0)=N1(x),

(4)

E(x+L,t)=E(x,t),N(x+L,t)=N(x,t)。

(5)

其中,未知复值函数E(x,t)为高频电场的包络波解,N(x,t)为未知实值函数是离子数密度在平衡态附近的扰动。1979年,C.Sulem和P.L.Sulem对一维Zakharov方程组的弱解的存在性进行了研究,解决了方程组的真实解的存在性问题[1]。1992年,R.T.Glassey利用差分法给出了一维Zakharov方程组的近似方程组, 验证了所给方程组具有守恒性质, 其收敛阶达到了步长的O(h2)[2]。1996～1997年,张法勇、向新民等利用Fourier拟谱方法对Zakharov方程组[3-4]和Schrodinger方程[5]进行了误差估计。2010～2012年,孙璐利用Fourier谱方法给出了半离散和全离散Fourier谱格式,证明了格式离散解的存在性和收敛性,得到了半离散Fourier谱格式解的稳定性[6-8]。文中主要借助谱方法[9]在时间和空间方向研究已建立的全离散Fourier谱格式离散解的稳定性。

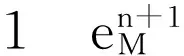
文中所用符号说明同文献[8]。

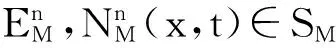
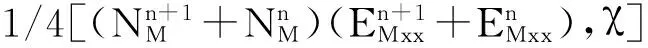
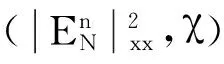
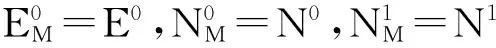
其中设

tn=nΔt≤T,En=E(·,tn),Nn=N(·,tn),

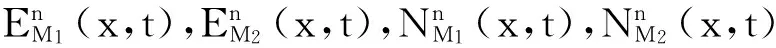
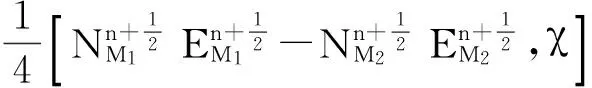
(6)

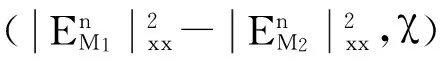
(7)

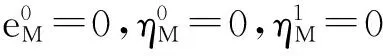
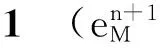
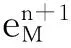
(8)

(9)

式(9)左边第一项,得

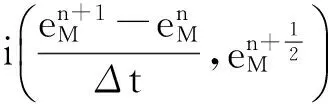
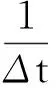
式(9)左边第二项,利用周期性,分部积分得

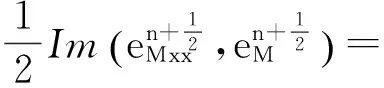
式(9)右端得

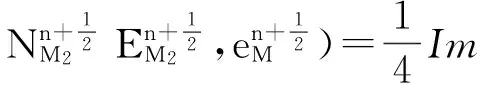
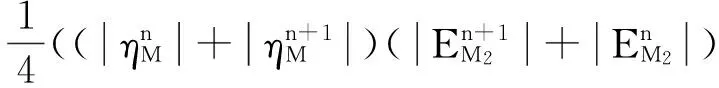
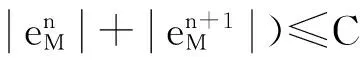
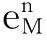
因为,

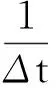
综上可知,

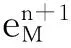
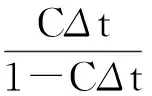
证毕。

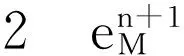
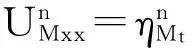
则有下面定理成立。

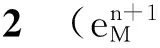
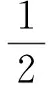
An-1+Bn-Bn-1)≤CΔt(Θn+Θn-1),

(10)

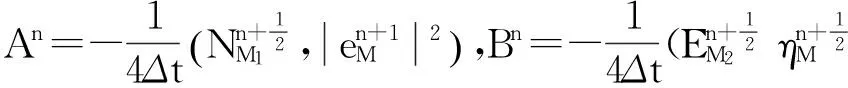
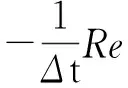
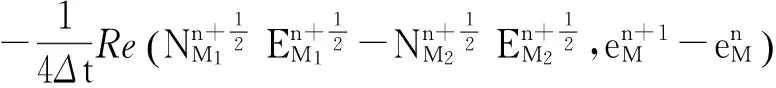
(11)

考虑式(11)等号左端第一项有

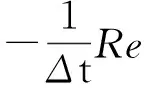
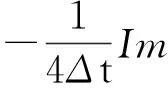
式(11)等号左端第二项,利用周期性,分部积分得

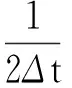
式(11)等号右端,

(12)

式(12)等号右端第一项:

(13)

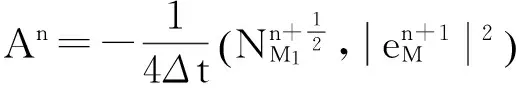
式(13)等号右端第三项:

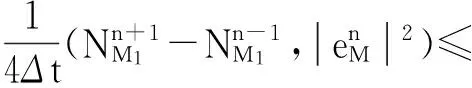
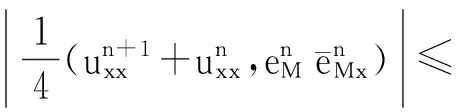
式(12)右端第二项:

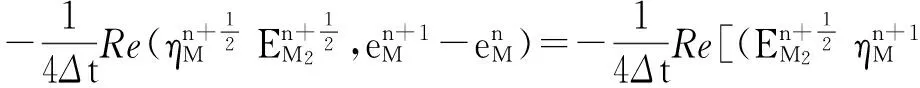
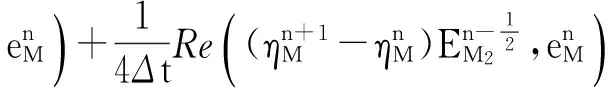
(14)

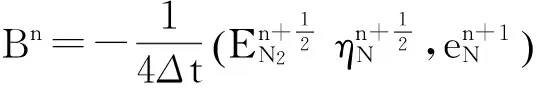
式(14)右端第三项:

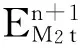
式(14)右端第四项:

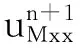
综上可知

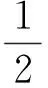
Bn-Bn-1)≤CΔt(Θn+Θn-1)。

证毕。

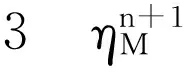
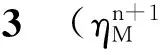
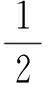
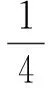
(15)

(16)

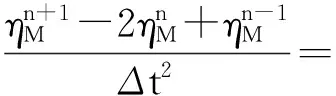
式(16)等号左端第一项,利用PM性质,Uxx=ηMt,分部积分得

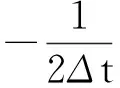
式(16)等号左端第二项,利用PM性质,分部积分得

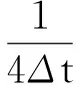
式(16)等号右端

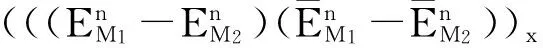
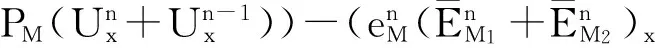
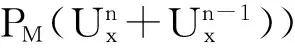
(17)

式(17)的第一项

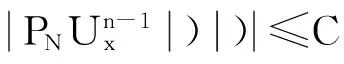
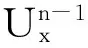
式(17)的第二项,

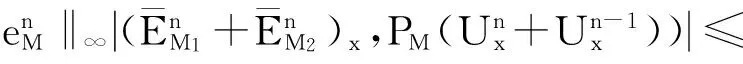
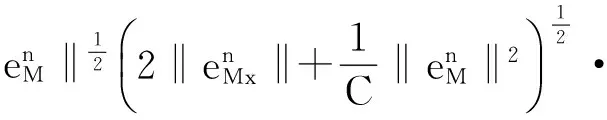
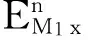
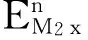
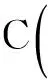
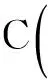
C(Θn+Θn-1),

综上可得

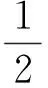
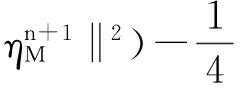
CΔt(Θn+Θn-1)。

证毕。

4　解的稳定性

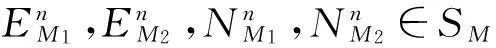
Θn≤CT。

证明设

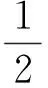
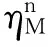
由式(10)+(15)得

Hn+ΔtBn+ΔtAn≤Hn-1+ΔtBn-1+

ΔtAn-1+CΔt(Θn+Θn-1),

(18)

由Θn的定义可知

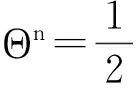
设

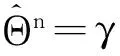
由定理1中式(8)以及式(18)可知

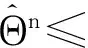
CΔt(Θn+Θn-1),

对于

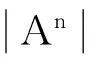
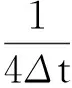
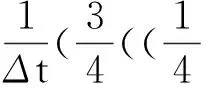
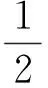
利用young不等式,再利用柯西不等式,可得

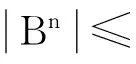
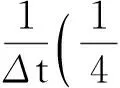
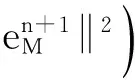
从而有

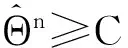
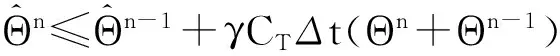
再有Θn的定义,有

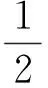
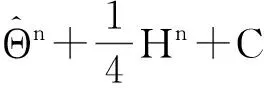
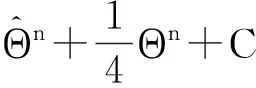
从而有

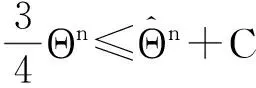
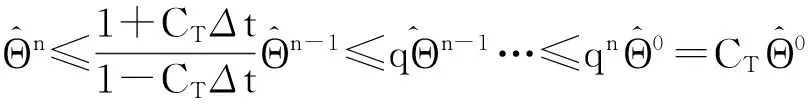
所以

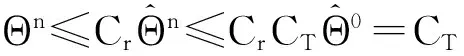
证毕。

从而可得

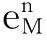
所以全离散解是稳定的。

5　结束语

文中研究Zakharov方程组全离散Fourier谱格式解的稳定性。在Zakharov方程组全离散格式的先验估计及误差估计的基础上,利用全离散格式所具有的守恒性质,验证了方程组的全离散Fourier谱格式解的稳定性,改进了Zakharov方程组半离散格式只在空间方向上讨论半离散解稳定性的不足,从而在时间和空间方向上得到了全离散格式的稳定性,进一步完成了全离散格式的解适定性的判别。文中所用方法的优点是全离散谱格式的解可以无限光滑,收敛阶的收敛速度可以达到无穷阶。该方法具有一定的普遍性,同样适用于动力系统中其他偏微分方程,可对不同偏微分方程进行时间和空间方向上的全离散,建立全离散谱格式,进而研究离散解的适定性。由于文中是在有限时间[0,T]内所做的研究,在无限时间区间内尚需讨论。

[1]SULEMC,SULEMPL.RegularitypropertiesfortheZakharovequations[M].Berlin:Springer, 1979: 123-149.

[2]GLASSEY R T. Convergence of energy-preserving scheme for the Zakharov equations in one space diminsion[J]. Mathematics of Computation, 1992, 1: 83-102.

[3]ZHANG FAYONG, XIANG XIMING. The global error estimate of the pseudospectral method for a class of generalized Zakharov equations(Ⅰ)[J]. Journal of Natural Science of Heilongjiang University, 1996, 13(2): 1-6.

[4]ZHANG FAYONG, XIANG XIMING. The global error estimate of the pseudospectral method for a class of generalized Zakharov equations(Ⅱ)[J]. Journal of Natural Science of Heilongjiang University, 1997, 14(3): 2-7.

[5]苏在滨, 张法勇, 范广慧. 带有弱阻尼项的非线性Schrodinger方程全离散Fourier拟谱格式的长时间行为[J]. 黑龙江大学自然科学学报, 2010, 27(03): 296-303.

[6]孙璐. Zakharov方程组的Fourier谱方法[D].哈尔滨: 黑龙江大学, 2010.

[7]孙璐, 张法勇, 朱捷， 等. Zakharov方程组半离散Fourier谱格式解的存在性[J] . 科技导报， 2012， 30(01)： 73-75.

[8]孙璐, 张法勇， 朱捷， 等. Zakharov方程组半离散Fourier谱格式的稳定性[J]. 黑龙江科技学院学报， 2011, 21(4)： 337-341.

[9]向新民. 谱方法的数值分析[M]. 北京： 科学出版社, 2000.

(编辑王冬)

Stability of full-discrete Fourier spectral scheme for Zakharov equations

SUNLu1,ZHANGFayong2,CHENHonghai1,WANGChun1

(1.College of Sciences, Heilongjiang Institute of Science & Technology, Harbin 150027, China; 2.School of Mathematical Science, Heilongjiang University, Harbin 150080, China)

Zakharov equations; Fourier spectral scheme; full-discrete; stability

1671-0118(2012)06-0640-05

2012-08-31

国家自然科学基金项目(19271025);黑龙江省教育厅科学技术研究项目(12523048)

孙璐(1980-),女,黑龙江省哈尔滨人,讲师,硕士,研究方向:微分方程数值解法,E-mail:adams-lulu@126.com。

O241.1

A