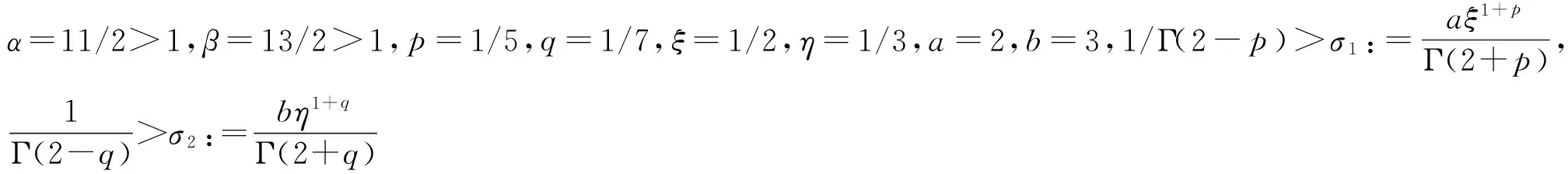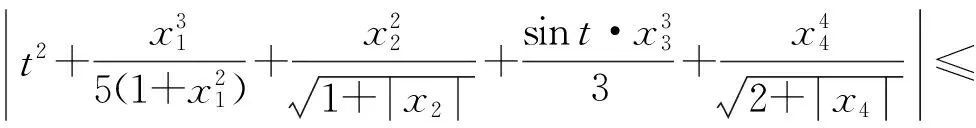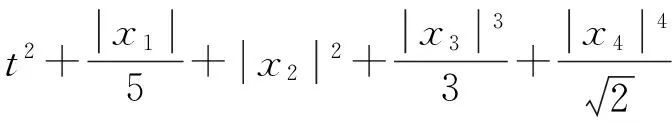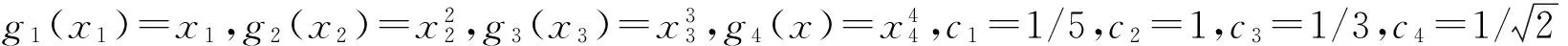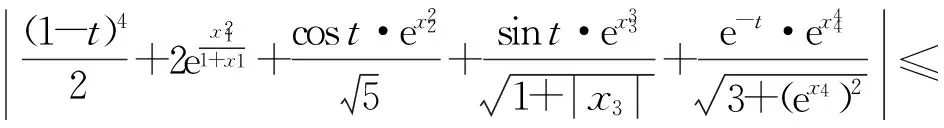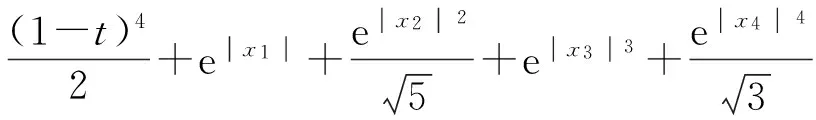分数阶微分方程耦合系统多点积分边值问题的解
2012-11-04史小艺
张 宁, 张 娣, 史小艺
(1.中国矿业大学 理学院, 江苏 徐州 221116; 2.中国矿业大学 管理学院, 江苏 徐州 221116)
分数阶微分方程耦合系统多点积分边值问题的解
张宁1,张娣2,史小艺1
(1.中国矿业大学 理学院, 江苏 徐州 221116; 2.中国矿业大学 管理学院, 江苏 徐州 221116)
文中讨论了一类非线性Caputo型分数阶微分方程耦合系统多点积分边值问题解的存在性。在一定条件下,给出格林函数,用Schauder不动点定理得到了解存在的充分条件。数值算例说明了所得定理的适用性。
分数阶微分方程; 多点边值问题; Green函数; 不动点定理
0 引 言
近些年来,分数阶导数及分数阶微分方程在科学、工程和数学等领域得到了重要应用,分数阶微分方程边值问题的理论研究,获得了不少研究成果[1-8]。值得注意的是,分数阶耦合系统多点边值问题作为分数阶边值问题的一种情况,近年来得到研究者们的重视[5-8],如文献[5]研究了分数阶耦合系统反周期边值问题
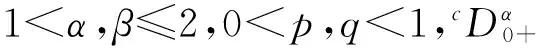
受上述文献启发,笔者利用不动点定理,研究一类非线性的Caputo型分数阶微分方程耦合系统多点积分边值问题(BVP)
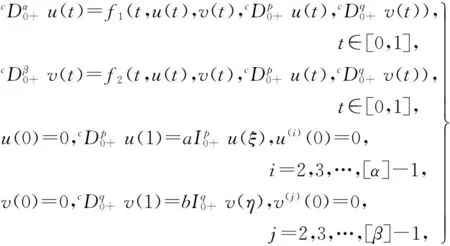
(1)
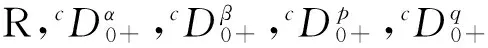
1 预备知识
定义1[3]函数u:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为
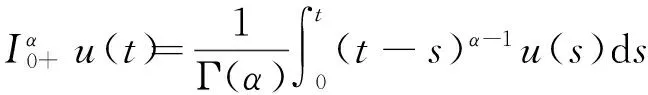
其中α>0,Γ(·)为Gamma函数。
定义2[3]函数u:(0,+∞)→R的α阶Caputo分数阶导数为
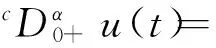
其中α>0,Γ(·)为Gamma函数,n为大于或等于α的最小整数。
引理1[5]令u∈Cm[0,T]且α∈(m-1,m],m∈N。那么对于t∈[0,T],
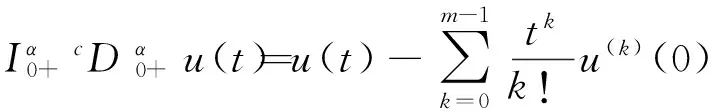
引理2假设y(t)∈C[0,1],那么分数阶微分方程边值问题(BVP)
(2)
等价于积分方程
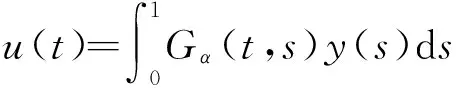
其中,
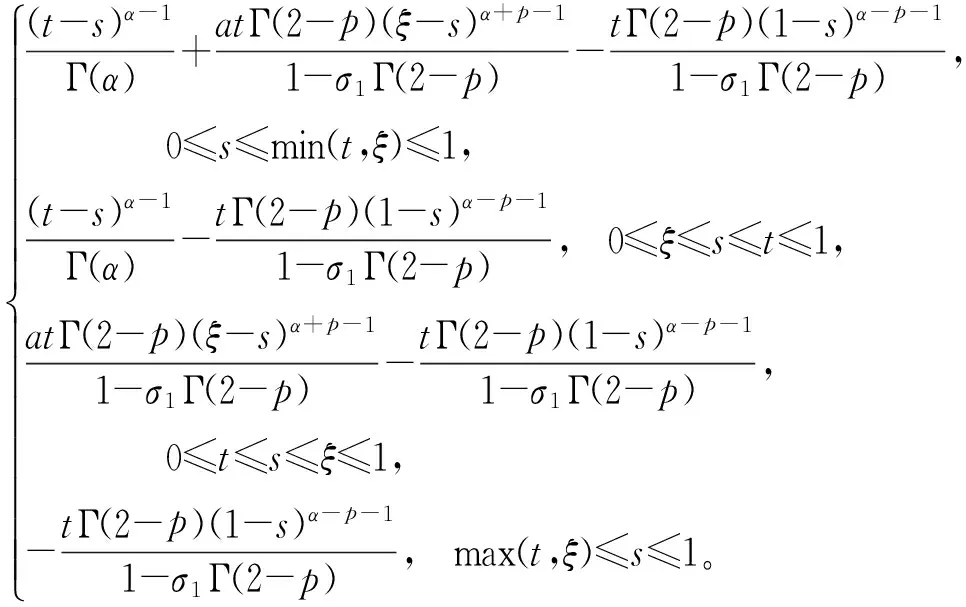
证明应用引理1,有
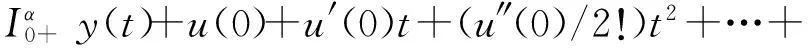
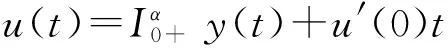
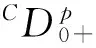
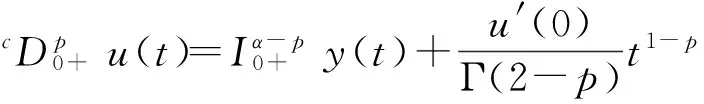
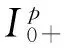
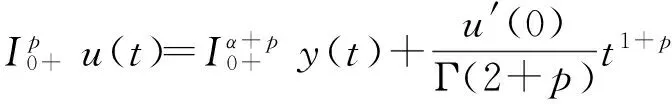
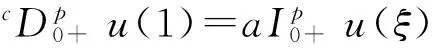
u′(0)=
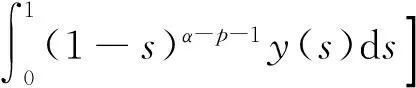
因此,
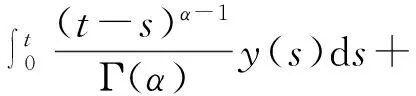
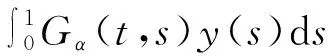
(3)
反过来,也很容易证明满足式(3)的解也是BVP(2)的解,得证。
2 主要结果

假设(u,v)∈X×X是BVP(1)的一个解,则
定义映射T:X×X→X×X,
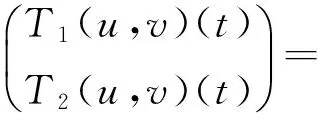
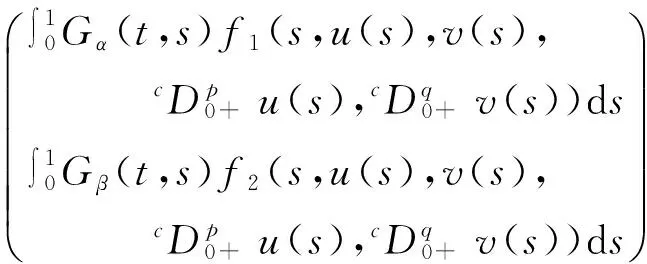
(4)
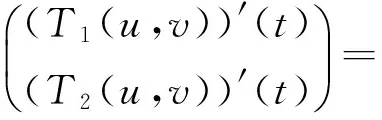
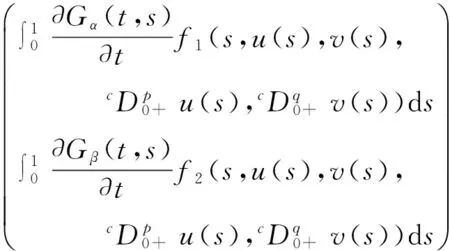
(5)
其中,
为方便,引入记号:
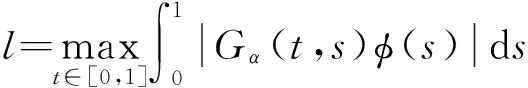
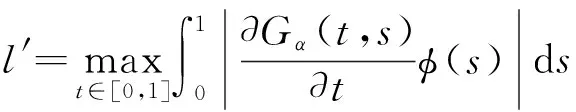
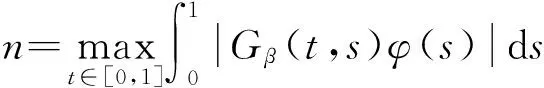
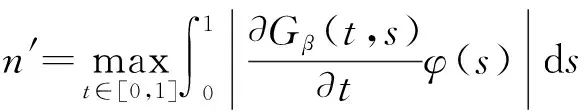
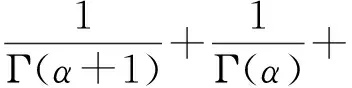
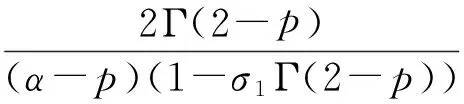
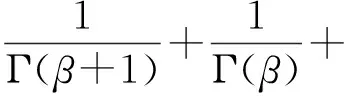

定理1假设下列条件成立,
(C1)f1,f2:[0,1]×R4→R是连续的;
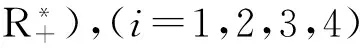
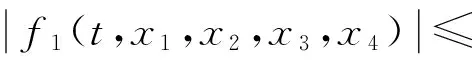
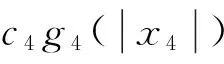
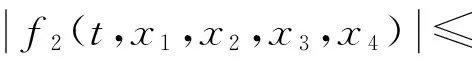
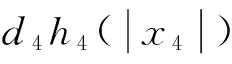
其中,常数ci,di>0(i=1,2,3,4),那么BVP(1)有一个解。
证明(1)先证明映射T:X×X→X×X是连续的。
对于0 因为 (2)定义Ω={(u,v)∈X×X:‖(u,v)‖≤r},取c1g1(r)+c2g2(r)+c3g3(r)+c4g4(r)≤(r/2-l-l′)/M,d1h1(r)+d2h2(r)+d3h3(r)+d4h4(r)≤(r/2-n-n′)/M′,证明T(Ω)是相对紧的。 ∀(u,v)∈Ω,由条件(C2),有 l+(c1g1(r)+c2g2(r)+c3g3(r)+c4g4(r))· l+(c1g1(r)+c2g2(r)+c3g3(r)+c4g4(r))· 同时有 l′+(c1g1(r)+c2g2(r)+c3g3(r)+c4g4(r))· l′+(c1g1(r)+c2g2(r)+c3g3(r)+c4g4(r))· 故‖T(u,v)‖≤r,即T(Ω)是相对紧的。 0≤t≤1,‖(u,v)≤r‖), 对于任意0≤t1≤t2≤1,有 同时有 同理可得 由于t1→t2,那么 都趋于0,所以T等度连续。由Ascoli-Arzela引理,知映射T:X×X→X×X是全连续的。再由Schauder不动点定理,知T有一个不动点,从而BVP(1)有一个解。 例1考虑边值问题 (6) 对于 [1]LIU XIPING, JIA MEI, XIANG XIUFEN. On the solvability of a fractional differential equation model involving thep-Laplacian operator[J]. Computers & Mathematics with Applications, 2012, 64(10): 3267-3275. [2]GUEZANE-LAKOUD A, KHALDI R. Solvability of a fractional boundary value problem with fractional integral condition[J]. Nonlinear Analysis: Theory,Methods & Applications, 2012, 75(4): 2692-2700. [3]CHEN TAIYONG, LIU WENBIN, HU ZHIGANG. A boundary value problem for fractional differential equation withp-Laplacian operator at resonance[J]. Nonlinear Analysis:Theory,Methods & Applications, 2012, 75(2): 3210-3217. [4]朱彦, 李鑫. 一类非线性分数阶微分方程三点边值问题的解[J]. 黑龙江科技学院学报, 2012, 22(1): 93-97. [5]SUN JIHUA, LIU YILIANG, LIU GUIFANG. Existence of solutions for fractional differential systems with antiperiodic boundary conditions[J]. Computers & Mathematics with Applications, 2012, 64(6): 1557-1566. [6]WANG GANG, LIU WENBIN, ZHU SINIAN, et al. Existence results for a coupled system of nonlinear fractional 2m-point boundary value problems at resonance[J]. Advances in Difference Equations, Springer, 2011, 2011(1): 44. [7]ZHANG YINGHAN, BAI ZHANBING, FENG TINGTING. Existence results for a coupled system of nonlinear fractional three-point boundary value problems at resonance[J]. Computers & Mathematics with Applications, 2011, 61(4): 1032-1047. [8]SU XINWEI. Boundary value problem for a coupled system of nonlinear fractional differential equations[J]. Applied Mathematics Letters, 2009, 22(1): 64-69. (编辑王冬) Solutions for multi-point boundary value problem of coupled system of fractional differential equations with integral boundary conditions ZHANGNing1,ZHANGDi2,SHIXiaoyi1 (1.College of Sciences, China University of Mining & Technology, Xuzhou 221116, China; 2.School of Management, China University of Mining & Technology, Xuzhou 221116, China) This paper discusses the existence of solutions to multi-point boundary value problem of a coupled system of nonlinear fractional differential equations with integral boundary conditions. In certain conditions, the study starts with Green’s function, followed by the sufficient conditions for the existence of solutions obtained by using Schauder fixed point theorem. The study ends with the illustration of the applicability of the theorem by a numerical example. fractional differential equation; muti-point boundary value problem; Green’s function; fixed point theorem 1671-0118(2012)06-0635-05 2012-05-17 国家自然科学基金项目(10771212) 张宁(1985-),女,山西省晋城人,硕士,研究方向:微分方程边值问题,E-mail:ninging_love@163.com。 O175.8 A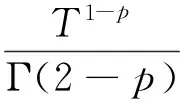
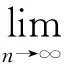
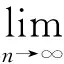
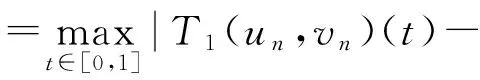
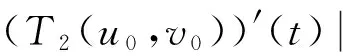
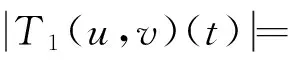
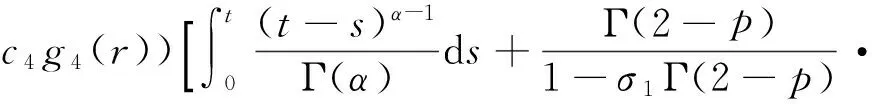
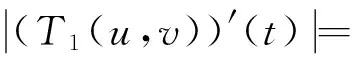
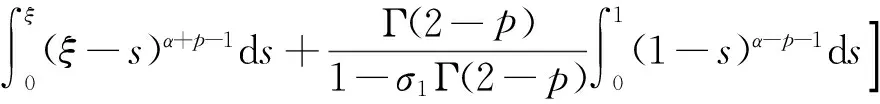
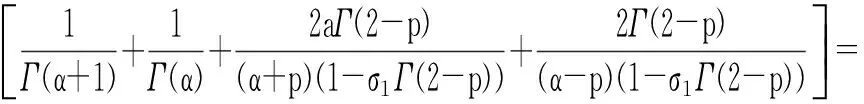
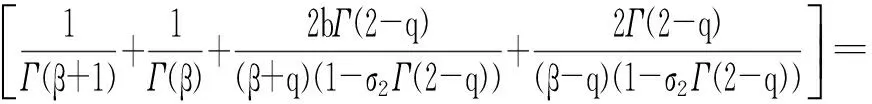
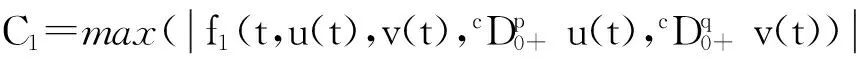
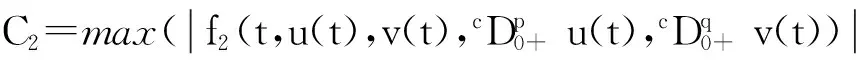
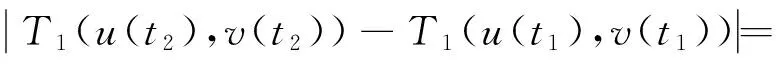
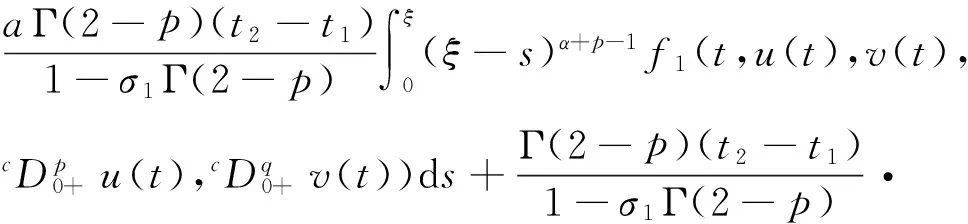
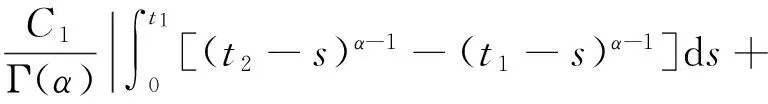
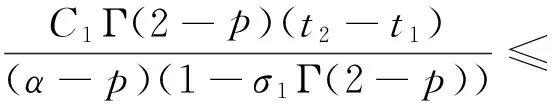
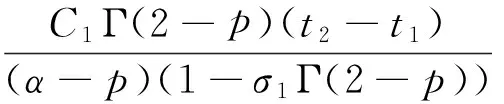
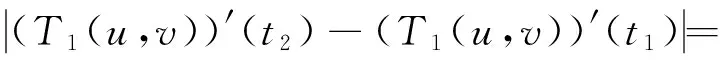
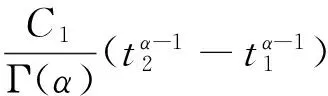
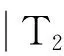
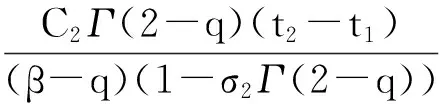
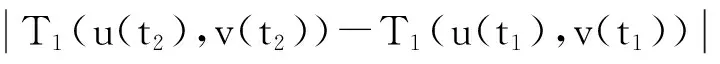
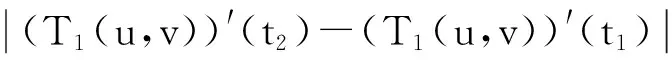
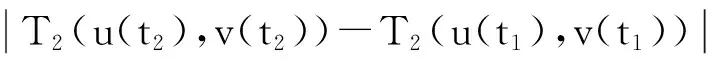
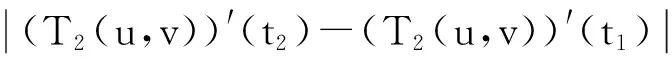
3 算 例