高三艺术生数学学习力提升探析①

2012-11-04崔卫球

当代教育理论与实践 2012年6期

关键词：题组普通班小题

崔卫球

(广东省中山市小榄中学，广东中山528415)

高三艺术生数学学习力提升探析①

崔卫球

(广东省中山市小榄中学，广东中山528415)

艺术班的高三数学复习有特殊性，主要表现在数学基础较差与高三数学复习时间短两方面。如何在“基础”与“时间”的双重挤压之下提升数学学习力是一个全新的课题。本课题以三角专题复习为切入点，根据“最近发展区”理论，采用“点对点”、“先分后合”与“先合后分”的三阶段复习模式，在衔接基础、反复与反馈、借力艺术等方面对提升高三艺术生数学学习力进行了有益的探索。

艺术班;学习力;三角复习

一问题的提出

学习力是学习动力、毅力、能力的统称。著名作家、教育家叶圣陶曾说“教是为了不教”，教学的最终目的就在于提升学生的学习力——“学是为了会学”。随着“艺考热”的不断升温，普通高中艺术班规模日益壮大，艺术班的数学教学也因此受到更多的关注。这里所指的“关注”除了要让学生获得上大学所需要的分数之外，更重要的是提升高三艺术生的学习力。

艺术班与普通班的数学教学有所不同。首先，由于高一、高二年级专业课学习的需要，挤压了一部分文化课教学时间，使得艺术班数学教学受到影响，数学基础相对薄弱。其次，由于高三第一学期艺术班全力准备术科考试，文化课无暇顾及，真正的数学复习时间实际仅有一个学期左右。受到基础与复习时间的双重制约，要提升高三艺术生的数学学习力，必须对高三数学复习进行特殊设计。

为了有效提升艺术班高三数学学习力，笔者选取三角专题作为突破口进行了实践探索。三角函数专题包括教材中的《三角函数》、《两角和与差的三角函数》与《三角恒等变换》三章内容，约占46课时，涉及17个高考考点。作为考查学生数式运算能力、数形结合能力与函数思想的特殊题型，是每年高考的必考热点。三角题在高考中约占17分，分值比重与教学课时比重基本相当。

笔者首先对所在学校的三个艺术班的153名学生进行问卷调查，得到几个主要选项的调查结果如下:仅5%的学生肯定“三角题能拿全部分数”，超过30%的学生表示“不会用公式，不会解三角题”，超过50%的学生表示“三角题会而不对，对而不全”。在表示“会而不对，对而不全”的学生当中，将“算错”与“粗心”作为自己主要的丢分理由。调查显示，学生对三角题不适应的主要原因是:“变形复杂”、“不会用三角函数的图象与性质”、“与其他内容(如平面向量、解三角形等)综合”，这些需要在高三复习中有针对性地加以解决。

二关于“提升学习力”与“有效教学”

对教学而言，“提升学生学习力”与“有效教学”有区别，又有联系。前者侧重教学目标，后者侧重教学过程，两者都强调了学生的主体性。现阶段国内外关于提升学习力的相关研究较少，但有效教学由来已久。“有效教学”起源于十六世纪的美国科学化运动。所谓“有效教学”，就是在符合时代和个体积极价值建构的前提下其效率在一定时空内不低于平均水准的教学。它主要包括三个方面:一是引发学生的学习意向、兴趣。教师通过激发学生的学习动机，使教学在学生“想学”、“愿学”、“乐学”的心理基础上展开;二是明确教学目标。教师要让学生知道“学什么”和“学到什么程度”;三是采用学生易于理解和接受的教学方式。有效教学的核心其实就是提升学生学习力的问题。

艺术生对三角问题普遍感到困难，其中有教材的原因，也有教学的原因。教学不到位或者要求过度，都会给学生的学习造成学习困难，导致无效教学，无法提升学生学习力。教育部课程改革专家组核心成员余文森教授认为:速度、收益、安全是有效教学必须考虑的三个问题，即有效性必须综合考虑这三个要素——提高学习效率、增进学习结果、强化学习体验。维果菠基的“最近发展区”理论认为:教育对学生的发展能起到主导作用和促进作用，但需要确定学生发展的两种水平:一种是已经达到的发展水平;另一种是学生可能达到的发展水平，这两种水平之间的距离，就是“最近发展区”。学生的“最近发展区”是一个动态的区间，离开“最近发展区”的教学都是无效教学。

基于以上认识，提升高三艺术数学学习力，必须结合艺术班实际，恰当定位复习目标，瞄准“最近发展区”，选择合适的教学模式，高三艺术班的数学复习有效性应区别于普通班。

三分“三阶段”实施艺术班高三三角专题复习

认知心理学认为，人的认识是“螺旋式上升”的。为此，笔者对高三艺术班的三角复习进行“三阶段”模式设计，强调“多反复，快反馈”，循序渐进，逐步提高。

(一)第一阶段:“点对点”再现式复习

所谓“点对点”复习，就是“知识点”与“能力点(基本题)”之间的对应训练，教师根据艺术生的实际采用表格的形式，罗列知识要点与相应基本题，帮助学生重新梳理基本知识与基本思想方法。

“知识点”以填空题的形式设计，目的是引导学生结合课本进行复习，弥补高一、高二基础薄弱的不足。基本题以一步或两步到位的题目为主，控制难度。通过设置“基本题”，让学生检验自己对“知识点”的掌握程度，消除知识盲区，实现复习情况的快速反馈。此阶段的复习模式如图1，艺术班模式为图中实线所示，普通班模式为虚线所示。

图1 点对点模式图

例1:

点评:艺术班“点对点”式复习与普通班采用的复习方式有明显区别。普通班可设置“多知识点对多相关题”的复习模式，确保“宽覆盖”，力求基础关一步到位;而艺术班受到基础与时间的制约，复习起点要更低，配套练习要少而精，确保复习的“短、平、快”。另外，由于解三角形、平面向量内容与三角函数问题联系密切，将它们纳入同一专题进行复习，可降低学生的复习难度。

(二)第二阶段:“先分后合”题组式训练

所谓“先分后合”题组，就是通过设计一系列子问题(分题)进行铺垫，由浅入深，最后达到解决与高考难度相当的目标题(合题)的目的。其基本模式为如图2所示，实线是艺术班的设计模式，虚线为普通班的设计模式。

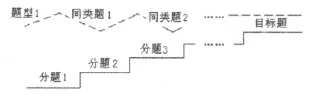
图2 先分后合模式图

由于艺术班与普通班学生的“最近发展区”不同，其题组设计的起点与标高应有所区别。普通班选题的灵活度与难度可以更大些;但艺术班的题组设计强调由浅入深，从易到难，分步达到解决“目标题”的目的。在“分题”的设置上，围绕解决“目标题”可能的障碍点与解题要点，分散难点，帮助学生领会基本思想方法，形成解题“套路”。

例2:

(1)函数y=Acos(ωx+φ)(ω＞0)的最小正周期是____;

(2)函数y=Atan(ωx+φ)(ω＞0)的最小正周期是;

(3)若函数f(x)=2cos2ωx－1的最小正周期与函数g(x)=tan的最小正周期相等，则正实数ω的值为__

22π，∴ω =

点评:本题组的前两个小题解决“目标题”——第(3)小题的两个基本点，从此入手，逐题深入，使(3)小题能顺利解决。“先分后合”题组式训练，较好兼顾艺术生数学基础薄弱的特点，“低起点，密台阶，小步走”，最后达到启迪思维、形成解题能力的目的。

(三)第三阶段:“先合后分”题组训练

所谓“先合”，就是减少前两个阶段教师指导过多的成分，让学生贴近实战，独立解决问题;所谓“后分”，就是教师依次给出难度更低的“同类题”或“变式题”，让不同层次的学生都找到自己能独立解决的“分题”。本阶段基本模式如图3，实线部分为艺术班，虚线为普通班。

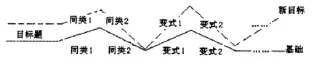
图3 先合后分模式图

艺术班的“先合后分”模式与普通班的后期“实战演练”有本质的区别。普通班更多着眼于新问题的解决，诞生新方法，提高陌生情境问题的解决能力;而艺术班更多强调让不同层次学生都有所发展，掌握通法通解，加强解题反思，回归基础。

1．艺术情境

艺术情境是“先合后分”的一种形式。结合艺术要素进行题组设计，可以激发艺术生的学习兴趣，提高复习效果。

例3:

(1)美国艺术基金会标志，通过简洁的正三角形传达出多重与基金会相关的意义(图4)。设图中正三角形边长为a，M、N、P是如图三角形顶点，则M与N的距离为__; cos∠MNP =___。

(2)如图5，在五个边长为a正三角形拼接而成的图形中，MN的长为___;cos∠MNP=___。

图4 美国艺术基金会标志

图5 正三角形拼接图

解析:(1)小题可以简化为(2)小题的形式解决。

在ΔMNP中，

MP=3a，NP=a，∠MPN=60°，

由余弦定理，得

点评:通过联系艺术，构造艺术情境，大大增加了数学问题的趣味性，激发艺术生的复习兴趣。

2．同类演练

同类演练题组是“先合后分”的又一种形式。通过同类题组的设计，让学生发现异同，消除易错点，提升解题能力。

例4:

解析:(1)，有x1x2+y1y2=2sinαcosα－sin2α +cos2α=sin2α+cos2α=0

∴tan2α=－1，∵α为锐角，∴0＜2α＜π，∴2α=，∴α=

(2)，有 x1y2－x2y1=－2sinαcosα－sin2α+ cos2α=－sin2α+cos2α=0

点评:两向量平行与垂直的充要条件是学生容易混淆的，通过题组设计让学生区分两个条件的异同，实现有效得分。

3．变式回归

变式回归题组是“先合后分”的又一种主要形式。先出示“目标问题”，后通过投影依次给出难度较低的“分问题”，让学生选择适合自己的“分问题”独立解决。教师由低到高的顺序讲评，兼顾了不同层次学生的发展水平。

解得

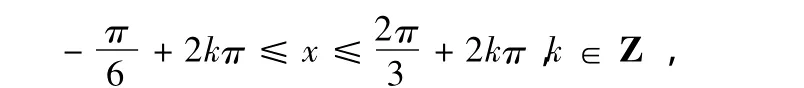
点评:本题组最后都归结为由整体角ωx+φ的范围，结合正弦函数的单调性解题。前3小题都可以变成第(4)小题的形式，第(1)小题要用到二倍角公式，第(2)小题是基本的“化一变形”，第(3)小题中x的系数为负是一个易错点。通过变式回归设计，满足了各个层次学生的不同需要，有利于学生发现解题规律，促使知识与能力的有效迁移。本题组的(2)小题另解上是增函数所求函数的单调区间为这样将角看作一个整体，结合正弦函数的图象求出x的范围难度大，普通班可用而艺术班不宜采用。

四 “三阶段”复习模式的初步成效与体会

(一)合适的教学是提升学习力的前提

“三阶段”复习模式符合艺术生的数学发展水平与特点，通过题组设计帮助学生安全跨越“最近发展区”，最后取得了良好的复习效果。因为“合适”，师生关系更加和谐，课堂“双边互动”更加充分有效;也因为“合适”，学生消除了解题恐惧感，解题信心明显增强，收获了超出学科本身的可贵的学习品质。

(二)“多反复，快反馈”是提升学习力的有效手段

一切教学设计都不能脱离学生的认知水平和规律。“三阶段”复习模式充分考虑了艺术生的特点，对接基础，多反复，快反馈，有效解决了“基础薄弱”与“复习时间短”的双重矛盾，取得了良好的复习效果。经过“三阶段”的训练，学生的“三角题能拿全部分数”达15%，“三角题会而不对，对而不全”仅剩30%，“不会用公式，不会解三角题”接近于0。